Квантовый выход состояния с разделенными зарядами в производных цинк-порфирина, возбужденных в состояние S2

Современная лазерная техника позволяет генерировать импульсы длительностью в несколько десятков фемтосекунд в достаточно широком диапазоне частот, что позволяет исследовать динамику фотоиндуцированных превращений молекул в реальном времени. Исследования переноса заряда с участием высших возбужденных электронных состояний выявили их характерную особенность: высокоэффективную рекомбинацию горячего состояния с разделенными зарядами в первое возбужденное состояние, которое в свою очередь может распадаться с повторным образованием состояния с разделенными зарядами [14; 16; 20]. Наиболее ярко эта последовательность переходов проявляется в характерной двугорбой кинетической кривой населенности состояния с разделенными зарядами, наблюдаемой экспериментально.

Такая последовательность переходов, включая горячие переходы, может быть количественно описана [12] в рамках многоканальной стохастической модели [7; 8; 15; 21; 23]. Эта модель позволила воспроизвести кинетики населенности состояний S 1 и S 2 для ряда ковалентно-связаных Zn-порфирин-имидных диад в растворе тетрагидрофурана, опубликованных в работе [14]. Позже модель была применена для моделирования кинетики населенности состояния с разделенными зарядами [3; 4; 18; 19]. Результаты такого моделирования [18] количественно воспроизводят характерные особенности экспериментальной двугорбой кинетическая кривой состояния с разделенными зарядами для Zn (II)-порфирин-нафталин-имида в растворе диме-тилформамида, которая была ранее измерена в работе [20]. Эти исследования не ответили на вопрос, можно ли использовать стохастическую модель для моделирования кинетики в неполярной среде.

Целью данной работы является воспроизведение двугорбой кинетической кривой населенности состояния с разделенными зарядами, наблюдаемой экспериментально, исследование влияния динамических свойств медленной внутримолекулярной моды на выход ионного состояния для диады Zn-порфирин-аминонафталин-диимид в растворе толуола в рамках обобщенной стохастической модели.

Для описания сверхбыстрого разделения зарядов из второго возбужденного состояния и последующей рекомбинации зарядов в первое возбужденное и основное состояния, используется минимальная модель, включающая четыре электронных состояния: основное состояние ( S 0 ), первое и второе синглетные возбужденные состояния ( S 1 , S 2 ) соответственно и состояние с разделенными зарядами ( CS ) (рис. 1).

Функция релаксации растворителя X ( t ) имеет вид:

N

X ( t ) — £ xe - '" ' ,

¹ - 1                                                                    (1)

где x — E ri / E rm ; T i и E ri - вес, время релаксации и энергия реорганизации i -й моды среды соответственно; E rm — ^ E ri ; N - число мод растворителя.

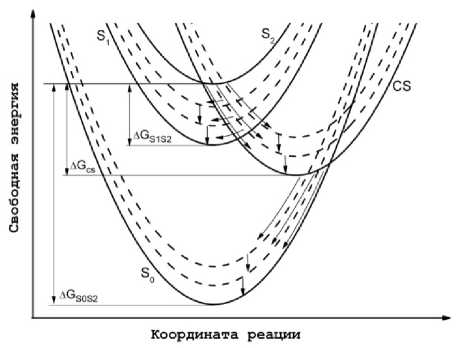
Рис. 1. Профили поверхностей свободной энергии основного S 0 , первого S 1 и второго S 2 возбужденных состояний, а также состояния с разделенными зарядами CS .

Пунктирные линии – колебательные подуровни CS , S 1 и S 0 состояний. Электронные переходы происходят на перекрестках всех подуровней

Диабатические поверхности свободной энергии электронных состояний в терминах координат реакции Q _i ( i -я координата соответствует i -й моде среды) могут быть записаны в виде [5; 7]:

N 2

US 2 = У —

S 2   = 4 E r.

,

• -               2

U(n) = у (Q 2 Er*) + A Gcs + Yna to CS                           CS

=1      4 Eria

• -    N 2)2M

U ( m ) = У — + A G_{S1S 2} + У m h^_a ,

S 1                         S 1 S 2

=1 4 Eri

• -    N  2)2M

• U (^' = У — + A G_S0 S2 + У l a^a ,

S 0                      S 0 S 2

i=1 4 Eri

где Qa и na, ma, la, (na, ma, la = 0, 1, 2,...) - частота и квантовые числа a-й внутримолекулярной колебательной моды соответственно, M – количество внутримолекулярных высокочастотных — — — колебательных мод, индексы n, m, l обозначают набор квантовых чисел n = {n1,n2,...na,...}, m = {m1,m2,...ma,...}, "7 = {l1,12,...la,...}, AGsоs2 - разность свободных энергий Гиббса между основным и вторым возбужденным состояниями.

В рамках стохастического подхода, обобщенного на случай многоуровневой системы, временная эволюция системы описывается системой дифференциальных уравнений (6)–(9). Этот подход применим для моделирования динамики разделения и последующей рекомбинации зарядов, когда вероятность горячего переноса электрона является значительной.

pS^} d t

^s 2 _— 5 t

л                 /          n

^{L s p} s 2 — Z ^к n I ^p s 2 - ^p cs „ n V

n

T      _( n ) . 7 CS f _

^— L CS ^p cs + к n V ^p s 2

—

p‘ ^{n p}cs j

k c ^ps 2 ,

—5n Z кn PCS +z n0 l lα

-⁽ n a ^{+ 1)} τ vα

^{CR f} o⁽ⁿ )       ^{m )} )

Z knn I pcs   psi I nm m

( n _α ^' )                 1         ( n )

^p cs   ^Z _T ( n a ) ^p cs ’

α

vα

—

d p sm)

5 t

— L s p s " — z к“ ( p s ⁿ ' — p * ) + 8 nn k c p_n + n m                     m m *

+Z

^ _T ( m a + α τ _{v α}

IT p sm" — Z α

1       ( m )

( m α ) ρ S 1 , τ _{v α}

^dps 0  — T „ _n ^{( l} ) . К _n(⁰⁾ . V ¹   O⁽ l a ) — V    ¹   r>( l )

— U ps 0 + k pCs +Z  (la +1) ps 0 Z  ,la ) ps 0, t                 l α τvα           α τvα где ps2 (Q• t) — функция распределения по координатам реакции во втором возбужденном состоянии; p^sm) (Q, t) - на m -м подуровне первого возбужденного состояния; ps0) (Q, t) - на l -м подуровне основного состояния; pC"s) (Q, t) - на n -м подуровне состояния с разделенными зарядами; вектора na, ma, la обозначают набор квантовых чисел na — {n1,n2,...na +1,...}, m'a — {m1,m2,...ma +1,...}, l'a — {11,12,...la +1,...}, m* - изоэнергетический с Us2 подуровень первого возбужденного состояния; Lˆ S и LˆCS – операторы Смолуховского, описывающие диффузию по термам US2, US1, US0 и UCS соответственно:

1 f, d /x->₂\ d² ^

7,, — / — 1 + Q --+ ( Q ) —7 I ^{,                         (10)}

L ^{s Z} T iV   ^i 5 Q i \^Vi /5 Q ² J

N 2

Lcs — У -1 1 + Q — 2 E —+ Q ■ Al                (11)

Lcs Z tV ( i ri !dQi \Vi /5Qi j где Op'S — 2ErikBT - дисперсия равновесного распределения по i-й координате; кIC - константа скорости внутренней конверсии перехода s2 ^ s 1. В этом случае инерционная компонента релаксации среды заменена дебаевской. Обоснование такой замены дано в работах [15; 16].

Зусмановские скорости переходов кCS — кCS(Q), кCn — кCR(Q) и кn— к(Q) - между n n          nm nm            l l термами Us2 и U(,n), Un) и Um), U(°) и U(1) соответственно. Для реакций разделения зарядов и CS CS       S1      CS       S 0

рекомбинации в основное состояние зусмановские скорости определяются выражениями:

k

CS

?

n

2 nV ?

/

=—5 и h ^{u U}

S 2

—

? A

и ⁽ n )

U CS ,

2      2 CS

^F ? ^F CS¹ ? ,

V

n

n

CCS  II

( S a^1CS ) ) n ^a

e—

. S a ⁽ CS >

n

П * nα

, S

( CS ) _

_E ( CS ) rvα

α

α

h^

k ?

l

2 nV ?

h

?

A

s и ( l )

S 0

—

^U CS ,

V

V ? ² l

2     CR 0

V CR 0 F ?

,

F C 0 II

( Sa⁽ CR 0 ) ) ^{l a} e

_ —1

I I α

α

- S a ⁽ CR 0 )

’ Sa

( CR о ) _

g ^{( CR} 0 ) rvα

h^ ’

для переноса заряда между состояниями CS и S1 выражения для зусмановских скоростей при- нимают более сложную форму:

k

CR

• ? ?

nm

2 nV ? ?

nm h

?

3 и ⁽ n ) ^u UCS

—

? A

TT ⁽ m )

US 1    ,

2       2 CR

^F ??    C CR¹ ?? ,

V

nm

nm

ⁿ a + ^m a —2 Г

FC nm

α

min( n _α , m _α )

X r=0

r!(nα

—

r)!(mα

— r)!

C ( CR )     E^ RR )

,    Sa          ho.a ,

где V _CR0 - электронные матричные элементы переходов | CS ^ ? | S 0^ , E rv _а - энергия реорганизации α-й высокочастотной колебательной моды соответственно. Индексы ( CS ) и ( CR ) соответствуют процессам разделения и рекомбинации зарядов.

Здесь предполагается одноквантовый механизм релаксации высокочастотной моды, переходы n _а ^ n _а - 1 протекают с константой скорости 1 / т? ) . Зависимость времени релаксации от номера колебательного состояния имеет вид т ^ О” ) = т ^ О ) / n _а [10].

Для формулировки начальных условий учтем, что возбуждение S 0 ^ S ₂ не сопровождается значительным перераспределением заряда. Это означает, что равновесное состояние полярной среды непосредственно после фотовозбуждения является хорошим приближением. Так как длина волны возбуждающего импульса, используемого в экспериментах, близка к красной границе полосы поглощения S ₀ ^ S ₂, то высокочастотная колебательная мода после перехода оказывается в основном состоянии. С учетом этого начальные условия принимают вид:

РS2(Q,t _ 0) _ П / 1 exp i 22к к)2}

—

^Qi ²

?                  ?

PCS’(Q,t _ 0) _ 0, pST’CQ,t _ 0) _ 0,

?

pS0’( Q, t _ 0) _ 0.

Система дифференциальных уравнений (6)-(9) с начальными условиями (12), (13) решалась численно с использованием ранее разработанных методов броуновского моделирования [6; 8; 9].

Населенности электронных состояний вычислялись по формуле:

P ( t )= LJ p'P ¹ ( 0 , Q г -.- Qn , * ) dQ i dQ 2- . dQ « ,                     ⁽¹⁴⁾

n где индексы i = S2, S1, S0 и CS.

В заключение схематично опишем физические процессы, которые учитывает модель. Возбуждение системы в состояние S2 визуализируется как появление волнового пакета в окрестности минимума терма S2 (см. рис. 1). После возбуждения системы в состояние S2 (рис. 1) протекают два конкурирующих процесса. Это внутренняя конверсия S2 ^ Si с константой скорости kIC и разделение зарядов, происходящие в точках пересечения термов US2 = UCS), и заселяющие колебательные подуровни состояния CS (пунктирные линии на рис. 1). Системы, образовавшиеся в состоянии CS, движутся к минимуму терма UC(nS) по мере релаксации среды. На этом этапе системы проходят точки пересечения термов US( 1m) и UC(nS) , что приводит к горячим переходам в первое возбужденное состояние S1. Кроме того, протекает внутримолекулярная колебательная релаксация, представляющаяся вертикальными переходами между соседними колебательными состояниями, UCS) ^ UCnS-1). Внутримолекулярная колебательная релаксация в состоянии S 1, USm) ^ USm-1), также играет важную роль, поскольку она может существенно увеличить эффективность горячей рекомбинации зарядов [15]. По завершении этих процессов населенности состояний S1 и CS могут быть далеки от равновесия. Далее населенности приближаются к их равновесным значениям в термическом режиме.

• 2.    Влияние динамических свойств медленной внутримолекулярной моды на кинетику населенности состояния с разделенными зарядами

В данном пункте представлены результаты фитинга двугорбой кинетической кривой населенности состояния CS, наблюдаемой экспериментально, исследование влияния динамических свойств медленной внутримолекулярной моды на выход ионного состояния для диады Zn-порфирин-аминонафталиндиимид в растворе толуола в рамках обобщенной стохастической модели.

Многоканальная стохастическая модель включает в себя много параметров. Часть из них достоверно определена для производных Zn-порфирина: разности свободных энергий между первым и вторым возбужденными состояниями A G S 1 S 2 = -0.8 эВ, между вторым возбужденным и основным состояниями A G _S о S ₂ = -2.9 эВ, свободная энергия разделения зарядов A G CS = -1.025 эВ. Скорость внутренней конверсии перехода S ₂ ^ S 1 составляет k IC = 0.5 пс^-1 [3; 20]. Динамические параметры растворителя толуола: x 1 = 0.59, x ₂ = 0.19, x ₃ = 0.22, т = 0.08 пс, т₂ = 0.65 пс, т₃ = 3.0 пс были измерены в работе [13]. Время релаксации внутримолекулярных высокочастотных колебательных мод предполагается равным τ _v ⁽¹⁾ = 0.1 пс.

Ранее было показано, что

при условии e = V e rv          rvα

= const и M = const скорость переноса

α заряда слабо зависит от спектральной плотности [12]. Это означает, что в качестве хорошего приближения для любого донорно-акцепторного комплекса можно использовать универсальную спектральную плотность, включающую 5–10 высокочастотных колебательных мод. При переходе от одного комплекса к другому изменяется только значение полной энергии реорганизации Erv. Значения Erva и ^Qа, используемые в расчетах, приведены в таблице 1.

Таблица 1

Параметры высокочастотных колебательных мод для переноса заряда

α	1	2	3	4	5	6	7	8	9	10
эВ	0.0558	0.0672	0.0744	0.1188	0.1602	0.1722	0.1782	0.1922	0.1947	0.2755
rv α , эВ	0.0126	0.0017	0.0034	0.0162	0.0673	0.0284	0.0380	0.2553	0.0263	0.1509

Варьируемыми параметрами при фитинге являлись энергия реорганизации среды E rm , полная энергия реорганизации квантовых внутримолекулярных колебательных мод E rv , матричные элементы для ионизации из второго возбужденного состояния V CS , рекомбинации в первое возбужденное состояние V CR 1 и рекомбинации в основное состояние V CR 0 .

Все попытки получить фитинг при различных значениях перечисленных параметров были неудачными. Основная проблема заключалась в очень маленькой ширине первого максимума, что приводило к нетипично большим значениям константы скорости распада состояния S 2 k CS’ .

Этот результат привел к необходимости предположить, что перенос заряда сопровождается реорганизацией медленной внутримолекулярной моды большой амплитуды. Такие моды являются релаксационными и могут быть описаны в рамках используемой здесь стохастической модели. Учет этой моды приводит к появлению дополнительного слагаемого в функции релаксации.

После попытки введения дополнительной моды в функцию релаксации (1), удалось получить достаточно качественный фитинг экспериментальной кривой CS. На рисунках 2 и 3 черными гладкими линиями представлен полученный фитинг, черными линиями с осцилляциями – экспериментальные кривые. Параметры фитинга: E rm = 0.90 эВ, E rv = 0.50 эВ, V CS = 0.025 эВ, V CR 1 = 0.045 эВ и V CR 0 = 0.0052 эВ. Параметры релаксационных мод: x 1 = 0.118, x 2 = 0.038, x 3 = 0.044, x ₄ = 0.8, т 1 = 0.08 пс, т₂ = 0.65 пс, т₃ = 3.0 пс, т₄ = 3.0 пс.

При таких параметрах были получены адекватные значения констант скорости: распада состояния S 2 k CS’ =5.52 пс^-1, разделения зарядов из S 1 k CS = 0.022 пс^-1 и рекомбинации зарядов в основное состояние k CR0 = 0.093 пс^-1.

Далее были проведены исследования, демонстрирующие зависимость выхода ионного состояния от параметров внутримолекулярной низкочастотной моды. На рисунке 2 представлены кривые кинетики населенности состояния CS для Zn(II)-порфирин-нафталинимида в растворе толуола, демонстрирующие влияние различных значений веса четвертой моды растворителя т₄.

Рисунок 2 показывает, что с ростом величины т4 квантовый выход ионного состояния падает. Данную особенность можно связать с ростом глубины провала на малых временах, что является прямым следствием роста эффективности горячей рекомбинации с ростом времени релаксации медленных мод [11].

В таблицах 2 и 3 представлены полученные константы скорости, характеризующие поведение полученных кривых.

На рисунке 3 представлены результаты моделирования, демонстрирующие влияние веса медленной моды растворителя x 4 на кинетику населенности состояния CS для того же соединения.

Этот рисунок показывает, что с ростом величины x 4 квантовый выход ионного состояния падает также как и с ростом т₄. Четвертая релаксационная мода является самой медленной, поэтому рост ее веса x 4 ведет к росту эффективного времени релаксации, вследствие чего и повышается эффективность горячей рекомбинации.

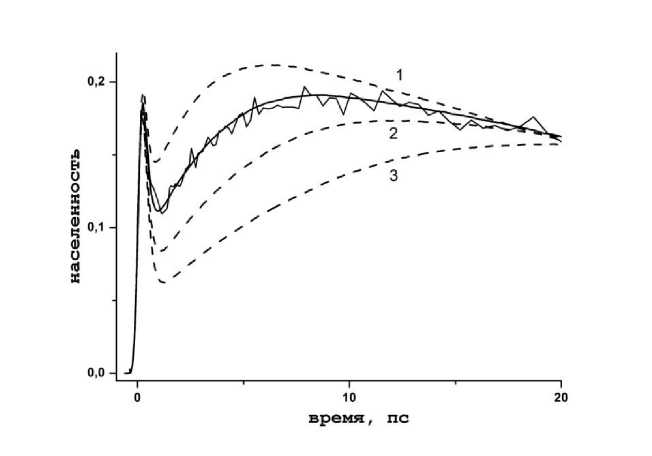
Рис. 2. Кинетика населенности состояния CS для Zn(II)-порфирин-нафталинимида в растворе толуола

Примечание. Черная линия с осцилляциями – экспериментальная кривая; черная гладкая линия – наилучший фитинг (параметры, при которых он был получен, указаны в тексте). Пунктирные линии соответствуют различным значениям т ₄: кривая 1 получена при т ₄ = 2 пс, 2 - при т ₄ = 5 пс, 3 - при т ₄ = 10 пс.

Таблица 2

Влияние времени релаксации медленной внутримолекулярной релаксационной моды т ₄ на кинетику электронных переходов

τ 4 , пс	2	3	5	10
k CS’ , пс-1	5.55	5.52	5.52	5.42
k CS , пс-1	0.029	0.022	0.016	0.01
k CR0 , пс-1	0.11	0.093	0.074	0.05

Таблица 3

x 4	0.7	0.8	0.9
k CS’ , пс-1	5.6	5.52	5.28
k CS , пс-1	0.027	0.022	0.17
k CR0 , пс-1	0.095	0.093	0.09

Представленные в таблицах 2 и 3 результаты имеют следующую интерпретацию. Скорость самого быстрого процесса разделения зарядов из второго возбужденного состояния протекает в фемтосекундной области и слабо зависит от времени релаксации медленной релаксационной моды. Этот процесс протекает в инвертированной области и его скорость слабо зависит от релаксационных характеристик среды [22]. Более медленный процесс рекомбинации зарядов в основное состояние значительно больше зависит от динамических свойств медленной моды растворителя т4. Скорость самого медленного процесса разделения зарядов из первого возбужденного состояния, протекающего в нормальной маркусовской области, в значительной степени определяется временем релаксации медленной моды т4. Это является свидетельством того, что разделение зарядов протекает в раствороконтролируемом режиме [22].

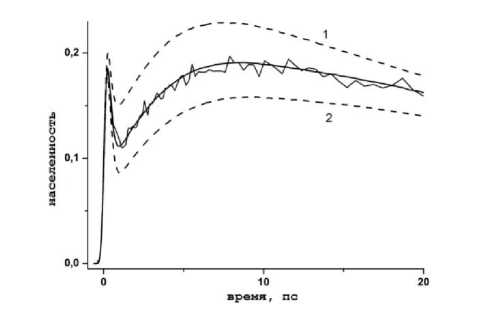
Рис. 3. Кинетика населенности состояния CS для Zn(II)-порфирин-нафталинимида в растворе толуола

Примечание. Черная линия с осцилляциями представляет измерение кинетики поглощения на частоте 650 нм, обусловленное поглощением радикал-катиона, черная гладкая линия – наилучший фитинг (параметры, при которых он был получен, указаны в тексте). Пунктирные линии соответствуют различным значениями веса четвертой моды растворителя x 4 : кривая 1 получена при x 4 = 0.7; 2 – при x 4 = 0.9.

Заключение . В работе исследовано влияние веса и динамических свойств классической внутримолекулярной моды на квантовый выход состояния с разделенными зарядами. Показано, что вариация параметров этой моды может значительно изменить квантовый выход состояния с разделенными зарядами, однако не настолько, чтобы получить 60 %, предсказываемые фитингом в рамках экспоненциальной модели [17].

ПРИМЕЧАНИЕ

• ¹    Работа выполнена при финансовой поддержке РФФИ (грант № 13-03-97062).