Квазидвумерная коэффициентная обратная задача для волнового уравнения в слабо горизонтально-неоднородной среде с памятью

1.    Введение. Постановка задачи

Как известно, учет памяти среды при распространении в ней упругих, акустических и электромагнитных волн, дает более точное описание процессов, происходящих в этих средах. Поэтому восстановление неизвестных характеристик для сред с последействием,

• ^# Работа выполнена в Северо-Кавказском центре математических исследований ВНЦ РАН при поддержке Минобрнауки России, соглашение № 075-02-2021-1844.

несомненно, является актуальной задачей. Для практических приложений более интересным является случай, когда характеристики среды зависят от двух и более переменных. Например, для геофизики одним из основных вопросов является количественная оценка горизонтальных неоднородностей в скоростях сейсмических волн. Накоплены факты, свидетельствующие о существовании внутри Земли неоднородностей по географичесим координатам, или горизонтальных неоднородностей. К числу таких фактов относятся систематические отклонения годографов волн от усредненного годографа, асиметрия гравитационного и электромагнитного полей. При этом отклонения от годографов, отвечающих сферически-симметричному распределению скоростей упругих волн, достаточно малы [1].

Целью данной работы является определение двумерного коэффициента и ядра интегрального оператора для волного уравнения в слабо горизонтально-неоднородной среде.

Для (x,z,t) € R ³ , z >  0, рассмотрим прямую задачу определения функции u(x,z,t) из интегро-дифференциального уравнения:

U tt - U xx — U zz — q ( x, z)u

t j. ■) utM,. —T)dr, 0

^U l t< 0     ⁰,

= — 5'( x )5' ( t ) , z =+0

• (1.1)

• (1.2)

• (1.3)

где £ ‘ (•) — производная дельта-функции Дирака; q ( x,z ) — коэффициент, характеризующий свойства среды, в которой распространяется волновой процесс; k ( t ) — ядро, описывающее память среды.

При заданных функциях q ( x, z) , k ( t ) задача (1.1)-(1.3) корректно поставлена и имеет единственное решение u(x,z,t), обладающее компактным носителем при любом конечном t.

Обратная задача заключается в определении коэффициента q(x,z), ( x, z) € R ² , z >  0 и k ( t ) , t >  0, входящих в (1.1), если относительно решения прямой задачи (1.1)-(1.3) известна дополнительная информация

u(x,z,t) | z =o = f (x,t), t> 0, x € R,

(1.4)

f (x, t ) — заданная функция.

Определение. Пара функций q(x,z), k(t) из класса непрерывных функций C (R + ) и C ( R х R + ) , соответственно, называется решением обратной задачи (1.1)-(1.4), если соответствующее ей решение прямой задачи (1.1)-(1.3) u(x,z,t) из класса обобщенных функций D ( R х R + ) удовлетворяет (1.4) для f (x,t) , принадлежащих классу функций D ( R х R + ) .

Задачи по определению ядер интегральных операторов — это интенсивно развивающееся направление в теории обратных задач. Первые результаты по данному направлению отражены в работах [2–8]. Одной из фундаментальных работ по определению ядер для гиперболических уравнений является монография [9]. В ней представлены результаты исследования корректности ряда постановок одномерных и многомерных обратных динамических задач. Литературные источники, представленные в монографии достаточно полно отражают исследования в области задач определения ядер. Из последних результатов в этой области можно отметить, например, работы [10–17].

Методика данного исследования базируется на развитых ранее методах исследований обратных задач для уравнений гиперболического типа [18–20]. В частности, в работе [19] рассмотрена одна модельная задача определения двумерного ядра интегро-дифференциального уравнения в среде со слабо горизонтальной неоднородностью, в которой развиты методы решения обратных задач из работы [18].

В работе [20] изучена обратная задача по определению двух неизвестных функций для уравнения, описывающего процесс распространения волн в полупространстве, заполненном средой. Было показано, что обе искомые функции одной переменной однозначно определяются заданием образа Фурье по переменной x решения прямой задачи на границе полупространства.

Предполагаем, что q(x, z ) слабо зависит от горизонтальной переменной х :

q ( x, z ) = q o ( z ) + Exq i ( z ) + O(e ² ),                             (1.5)

где E — малый параметр. В дальнейшем будем полагать в равенстве (1.5) q o (z) = q o > 0 есть известная величина.

Решение прямой задачи (1.1)–(1.3) будем искать в виде ряда по степеням ε :

∞

u(x, z, t ) = У^ E j U j (x,z,t).                                (1-6)

j =0

Тогда, учитывая (1.4) и (1.6), имеем

∞ f (x,t) = ^ Ej fj (x,t).                                 (1-7)

j =0

Нетрудно проверить, что u j (следовательно и f j ) — нечетные по x при четных j и четные — при нечетных j . Тем самым, по известной функции f (x,t) можно найти f o (x,t) и f i (x,t) с точностью до O ( e ² ) :

_ ^{f (x,t)} - ^{f ( - x,t)}        f-t ^{(x,t) + f( - x,t)}

J o ^(x,^t)                 2             , ^J i ^(x,^t)                 2             ^-

Подставляя (1.5), (1.6) в (1.1)-(1.4) и приравнивая коэффициенты при Ej, j = 0,1, получаем две обратные одномерные задачи последовательного определения k(t) и qi(z), которые будут рассмотрены в параграфах 2 и 3 соответственно. Для решения обратных задач достаточно задать образ Фурье от функций fo(x,t) и fi(x,t) по переменной х для фикисированного ненулевого значения параметра преобразования. Результатами исследования являются теоремы однозначной локальной разрешимости решения обратных задач.

• 2.    Задача определения u o (x,z,t) и k(t)

Рассмотрим прямую задачу определения u o (x,z,t) из следующей начально-краевой задачи:

t

(u o ) tt = (u o ) xx + (u o ) zz + q o • U o - j к ( т ) u o ( x,z,t - T ) dT,     ( x,z,t ) e R ³ , z> 0, (2.1)

uo lt<0 = 0,

= —5‘(x)5‘(t).

^dz z =+0

Применяя преобразования Фурье, получаем

t

(Uo)tt = (uo)zz + (qo — v2)uo - j к(т)Uo(v, z, t - т) dт, z > 0, t E R,

- ¹ _ _n duo u ^{o |} t< o ⁰, dz

= — iv5'(t),(2

z =0

где u o (v, z, t) = F x [u o ](v, z,t) := J^ u o ( x, z,t ) e^{-l vx} dx.

Обратная задача 1. Найти u o (v, z,t) и k(t) , входящие в (2.4)-(2.5), если u o (v, z,t)

для некоторого ненулевого значения параметра ν известно uo(v,z,t)|z=o = ivd(t) + fo(v,t) 9(t), t E R,                       (2.6)

где f o (v, t) = F x [f o ](v, t) — заданная функция, 6 ( t ) — функция Хевисайда (далее знак ⁷ над функциями u 0 , f 0 будет опущен).

Будем искать решение (2.4)–(2.5) в виде uo(v, z, t) = iv5(t — z) + v(v, z, t) 9(t — z).

(2.7)

Тогда, подставляя (2.7) в (2.4)–(2.5) и применяя метод выделения особенностей [21], относительно функции v(v, z,t) получим

	t - z
v tt — v zz — (q o — v 2 )v =	— ivk(t — z) — У к(т)v(v, z, t — т) dT, 0	t > z > 0,	(2.8)
∂v ∂z	n 1           ivz /        2A = 0,   v| t = z = 7T (q o — v )• z =o                     2		(2.9)
	v| z =o = Mv,tY		(2.10)

Введем новые переменные zi := t + z, ti := t — z и пусть тт, + \      ( zi — ti zi + tiA

U^(v,z i ^,t i ^{) :}= v I ^v, —2—, —2— /.

Задача (2.8)-(2.10) перепишется в терминах функции U(v, z i , t i ) следующим образом:

_∂ 2 _U

∂t 1 ∂z 1

t 1

( q o — v ² ) U(v, z i ,t i ) — ivk(t i ) — У к(т)U(v, z i

— т, t _i — т) dT

(2.11)

U = / o ^(v,z i ⁾, t 1 = z 1

(2.12)

∂U

∂z 1

t 1 = z 1

= 2(f o ) Z i (v.z i ),

(2.13)

U к=0

- i^^ ( q o - v 2 ) .

(2.14)

Из (2.14) следует, что f o (v, 0) = 0. Пусть

w ( v,z i ,t i ) = |U(v, z i ,t i ), w(v, z i , 0) = - iv — ∂z 1

-

ν ²

,

тогда

z 1

U (v,z i ,t i ) = f o (v,t i ) + j w^kt i ) ^d6

t 1

(2.15)

Из уравнения (2.11) выводим z1

z 1

У^dT^dT = 4/ ⁽q o ^{- v 2 )U(v,}z i ^,T)

t 1

t 1

τ

- ivk ( T ) - У k(n)U(v, z _i

-

η, τ

-

n ) dn dT.

Так как

/" 1 d^^     1_ffV(

w ( v, Z 1 ,t i ),

dTdT = 2 fok (v,zi)- t1

то для w ( v,z i ,t i ) имеем

W^z i^i ) = |^(f o ^{) ,} z i ^(v,z 1 )

z 1

-

4 У ( q o ^{- v 2} ) U^(v,z i ^,T)

t 1

τ

- ivk ( T ) - У k(n)U(v, z _i

-

η, τ

-

n)dn dT.

(2.16)

Взяв t = 0 в уравнении (2.16) и дифференцируя его по z i , получим

1(f o ) Z 1 (v,z i ) =

z 1

4 У ( q o ^{- v} 2м

τ

’v, zi, t) - У k(n)^(v, zi - n, t - n) dn z1

dτ

+ 4 ( q

i o ^{- v}2)^f o ^(v, z i ) ^-

ivk ( z i ) - У k(n)f o (v, z i - n) dn .

Отсюда выводим уравнение для k ( z i ) :

2г

k(z i ) = V (f o )" (v,z i )

-

q 0 - ν ² i

ν

z 1

f o (v, z i ) + v у k(T)f o (v, z i - T) dT

z 1

-

V У (q o - v²М

τ v, zi,T) - У k(n)^(v, zi

(2.17)

-

η, τ

-

n) dn dT.

Теорема 1. Пусть T > 0 фиксировано и выполнены следующие условия: f o (v, 0) = 0 , (f _o ) t (v, 0) = - iv q ⁰^, f _o (v,t) G C ² [0,T] для некоторого ненулевого значения параметра v. Тогда обратная задача (2.4) - (2.6) в области G t = { (z, t) : 0 С z С t С T - z } имеет единственное решение k(t) G C[0, T] .

<1 Заметим, что в условиях теоремы обратная задача (2.8)-(2.10) эквивалента замкнутой нелинейной системе интегральных уравнений Вольтера второго рода с непрерывными ядрами и непрерывными свободными членами (2.15)–(2.17). Это показывается переходом от начально-краевой задачи (2.8)–(2.10) к системе (2.11)–(2.14), и далее к уравнениям (2.16), (2.17). Равенство (2.15) очевидно и используется для замыкания системы. Нетрудно убедиться, что и обратные преобразования имеют место [20].

Систему (2.15)–(2.17) можно переписать в виде

(2.18)

V = AV, где A := (Ai, A2, A3) — нелинейный оператор, действующий на множестве вектор-функ-ций v € C [GT],

V := [ U (—, z i ,t 1 ^ , ^(—, z i ,t i )_; к!%) ]. ϕ 1             ϕ 2          ϕ 3

Вид A 1 , A 2 , A 3 определяется правыми частями равенств (2.15)–(2.17). В качестве малого параметра данная система (2.18) содержит промежуток интегрирования, который не превосходит число T . Поэтому при малых T к ней применим принцип Банаха, обеспечивающий существование единственного решения системы. Действительно, пусть Q ( V o , I v oII) =: { v : llv - V o I <  I v o I} — шар радиуса I v o I с центром в точке v o пространства непрерывных функций, где вектор-функция

-

(q^ f o ( v.z ₁ )

■—^^^^^^^^^^^^^^^^^ ϕ03

V o ^(—,z 1 ) ^:= ^f o ^(v,t 1 ^), jc/ol^ ^(v,z i ), 2;(fo^ ^(v,z i )

^01^ '-' ^

ϕ 02

и

H v o H = ^max {^Н , il V 02 II, II V 03 11} , 1Ы1 ^:= h • H c [ g _t ] .

Нетрудно заметить, что для v € Q ( v o , I v o I ) имеет место оценка

I v I < I V o I + I v o I <  2 | v o | .

Пусть v ( v, z i ,t i ) € Q(v o , I v o I ). Покажем, что при подходящем выборе T оператор A переводит шар в шар, т. е. Av € Q(v o , I v o I ) . На самом деле, составляя норму разностей с помощью равенств системы (2.18), для (z, t) € G T имеем

IAV - Vo I = sup |av - Vol < aIvo I, (z1,t1)∈GT где

^a = ^ [ q o ^{+ — + I f} o ^{I + 2 T I v} o ^I] ,

^ = 2 T max ^ 1, — ^ .

Очевидно, что существует такое T * , при котором a < 1 и для T € (0, T * ) оператор A переводит множество Q в себя.

Пусть теперь v ¹ , V 2 — любые два элемента из Q(v o , I v o I ). Тогда, используя вспомогательные неравенства вида

IV1V1 - V2V21 < Iv11 |V1 - V21 + |V21 Iv1 - V21 < 4IVoI llv1 - v2^, получим

lAv1 -AV2| < a Iv1 - V21, где а = 2 ^[qo + v + fo1 + 4T ^ Ш ‘

Заметим, что из условия а <  1 следует а <  1 . Поэтому можно сделать вывод о том, что оператор A является сжимающим на Q(^ o , ||^o ^ ) . Тогда согласно принципу Банаха уравнение (2.18) имеет и притом единственное решение в Q(^ o , | ^ o ||) при T Е (0, T * ) .

Решая систему уравнений (2.18) методом последовательных приближений, можно однозначно построить в области G t для T Е (0 ,T * ) вектор-функцию у и тем самым определить функцию k ( t ) Е C [0, T] [9]. >

• 3.    Задача определения u i (x,z,t) и q i ( z )

  Рассмотрим прямую задачу определния u i ( x,z,t ) из следующей начально-краевой задачи:

  t (u i ) tt = (u i ) zz + xq i (z)u o + q o u i — j к ( т ) u i ( x,z,t — т ) dT,             (3.1) 0

  (3.2)

  
  

  u i \t< о = 0,            = 0, z> 0, ( x,t ) Е R.

  t< 0

  ^∂z z =0

  
  

Обратная задача 2. Найти u i ( x,z,t ) и q i( z ), входящих в (3.1)-(3.2), если относительно преобразования Фурье F _x [ u i ]( v, z,t ) для некоторого ненулевого значения параметра ν известно ___ Г И Z               X I                    ~ Z

F x ^[u i ^](v,z,t) \ z =₀ = ^f i (^v,t), t> 0.

После преобразования Фурье по переменной x имеем (далее знак ⁷ над u i (v, z,t) , f i (v,t) будет опущен)

(u i ) tt = (u i ) zz + iq i (z)(u o ) V (v, z,t) + (q o — v2) u i (v, z,t) t

(3.3)

— У к ( т )u ₁ (v, z,t — т ) dT, z> 0, t Е R,

I - n   dui u1\t<0    0,    dz

u i \ z =0

— ⁰, ^u 1 | t = z — ⁰, z =0

= ^f 1 ^(v, t)-

(3.4)

(3.5)

Пусть Z 2 := z + , t 2 = t ^ z и U * ( v,Z 2 ,t2) := u i (v, Z 2 - t 2 ,Z 2 +1 2 ), тогда задача (3.3)-(3.5) перепишется в терминах новой функции U * (v, Z 2 , t 2 )

∂ ² U ^∗

∂t 2 ∂z 2

i

= 2 q i ^(z 2 ^— t 2 ) [ i^^(2t 2 ^{) + U} V ^(v, ^2z 2 , ^2t 2 ⁾9^(2t 2 ) ]

⁺2 ^^q o ^{— v 2} )U * ⁽

2t v, Z2,t2) — j к(т)U*(v, Z2 — T,t2 — T) dT ,

(3.6)

^U * \ t 2 =0 = ^{0, U} * \ t 2 = Z 2 = f 1 (v, 2Z 2 ),

(3.7)

∂U ^∗

∂z 2

С учетом (3.8) очевидно, что

Из уравнения (3.6) имеем

z 2

∂U ^∗

∂τ ∂z 2 t 2

z 2

t 2 = z 2

= ^(f 1 ) z 2 ^(v' ^2z 2 )•

z 2

∂U ^∗

-^ ( ^v,^'t 2 ) ^d^

t 2

z 2

-2 / ^q i ( z 2 - ^Т ) ⁵ (2 т ) dT + f / ^q i ( z 2 - T )U^( v, 2 Z 2 , 2 т ) dT

t 2

t 2

(3 . 8)

(3^9

+ 2

z 2

/ z

t 2

С другой стороны,

z 2

/ t 2

2 τ

- V ² )U * ( v, Z 2 ,T ) - У k ( n ) U * ( v, Z 2

^Гд   ^(v' z 2 '^T ) ^dT = ^(f l )' z ₂ ^(v' ^2z 2 ⁾

(3.10)

-

-

η, τ

-

n) dn dT.

∂U ^∗

.■      ^(v'^{Z 2} '^{t 2} )'

(3.11)

z 2

dU*          .    ,      ,      .    1 , . if,

--  (v,z2 't2) = (fi)z2 (v' 2z2) + -qi(z2) -- qi(z2 - T )Uv (v' 2z2'2t ) dT dz2                            4         2 J t2

z 2

-

2 j ( q o ^{- v 2} ) UC

t 2

Так как в силу (3.7)

2 τ

’V, Z 2 ,T ) - У k ( n ) U * ( v, Z 2

(3.12)

-

η, τ

-

n ) dn dT.

∂U ^∗

∂z 2

то взяв в (3.12) t 2 = 0 , выводим

= 0 , t 2 =0

z 2

q i ( z2^ = -4( f i )' z 2 ( v, 2 z 2 )+2 i У q i ( z 2 - т ) U^ ( v, 2z t , 2 т ) dT

+ 2 /^: ( q o - v ² ) U • ( 0

2 τ

V, Z 2 ,T ) - У k ( n ) U * (v, Z 2

(3.13)

-

η, τ

-

n ) dn dT.

Подставляя (3.12) в (3.11), получим уравнение для U * ( v, Z 2 ,t 2 ) :

z 2                    z 2 ξ

U *(v,z2,t2) = f1(v' 2z2) + 41 qi(^) d< - 2 У У qi(C - t2)U‘ (v' 2C' 2t ) drdc t2                        t2 t2

z 2 ξ

2 τ

(3.14)

- 2 J j [( q o - v 2 )U * ( v,^,^T ) - У k(n)U * ( v,e -

n, т - n ) dn^ dTd^.

t 2 t

Уравнения (3.13) и (3.14) являются замкнутой системой относительно q i (z 2 ) и U * ( v, Z 2 ,t 2 ) .

Теорема 2. Пусть T Е (0,T * ), f i (v,t i ) е C ⁱ [0,T] , f i (v, 0) = 0 , (f i ) t (v, 0) = 0 , и функции u o ( v,z,t ) и k ( t ) являются решением задачи (2.4) - (2.6) . Тогда в области G t существует единственное решение обратной задачи (3.13) - (3.14) q i (z) Е C [0,Т/2].

<1 Обратная задача (3.3)-(3.5) эквивалентна системе интегральных уравнений (3.13), (3.14). Данная система является замкнутой линейной системой интегральных уравнений Вольтерра второго рода с непрерывными свободными членами и ядрами относительно неизвестных функций в области Gt при v Е R. Идея доказательства существования единственного решения данной системы состоит в применении обобщенного принципа сжатых отображений [22]. Запишем систему (3.13), (3.14) в виде операторного уравнения ф = Бф,

(3.15)

ф :=

q i (z 2 ), U * ( v,Z 2 ,t 2 )

ψ 1           ψ 2

Линейный оператор Б = (Bi, Б2) определен на множестве вектор-функции ф Е C(R х Gt) и Bi, Б2 определяются правыми частями уравнений (3.13), (3.14). Покажем теперь, что некоторая степень n (n — натуральное число) линейного отображения Бф является сжатием. Положим Dt := [0,T/2] х [0,T/2] и j = 1, 2}.

^^ (v )=maxj max | ф j (v, Z 2 ,< 2 ) ! , ( Z 2 ,t 2 ) G D T

Пусть ф(1), ф(2) — две непрерывные вектор-функции в R х Dt , удовлетворяющие линейной системе интегральных уравнений (3.15). Для (v, Z2,t2) Е R х Dt имеем max |Bjф(1) - Bjф(2) |(v, Z2,<2) ^ Mz2^ф(1) - ф(2) ||, (v,Z2,t2) Е R х Dt, где M — константа, зависящая от величин T, ||UV||, qo, v, ||k(t)|. Далее

B^№

z 2

- Б ² ф ^{(2) |} (v,z₂,t 2 ) ^ M ² I ^ ^| ф ⁽¹⁾ - ф ⁽²⁾ || d^ o

< M ²| | ф ⁽¹⁾ - ф ⁽²⁾ | ,

j = 1,2.

Отсюда z2

max|Bnф(1) - Bnф(2)|(v,z2,t2) ^ M2 ПрФ^) - Ф(2)|, (z2,t2) Е Dt , и, вообще, ||Bnф(1) - Бпф^2 || < Mn (T^2) ||ф(i) - ф(2) ||. При любом фиксированном T число n можно выбрать настолько большим, что

M ⁿ

(T/2) ⁿ n!

< 1.

Тогда отображение B ⁿ является сжатием. Согласно обобщению принципа сжимающих отображений уравнение Bф = ф имеет одно и только одно решение, принадлежащее

C ( R x D t ). Данное решение может быть найдено методом последовательных приближений. ⊲

Формулы (2.15)–(2.17) и (3.13)–(3.14) служат основой для численной реализации алгоритма определения значений коэффициента q ( z ) . Подробное описание аналогичного алгоритма предложено в монографии [23, гл. 5], где в области D T вводится равномерная сетка с шагом h = T/ (2 N ) , N — количество узлов разбиения отрезка [0,Т/2] . Затем в формулах (2.15)–(2.17), (3.13)–(3.14) интегралы заменяются квадратурными формулами прямоугольников. Значения функций в узлах сетки находятся по рекуррентным формулам [23]. Результаты расчетов функций k(t) , q i (z) представлены на рисунках 1 и 2 соответственно при следующих значениях входных данных: T = 4 , q o = 0.5 , v = 1, f (v,t) = v ( t ² - i ^q 0 - ₂^v- 1) . На рисунке 2 — графики коэффициента q i (z) (c учетом ядра памяти — пунктирная линия, без учета — сплошная линия).

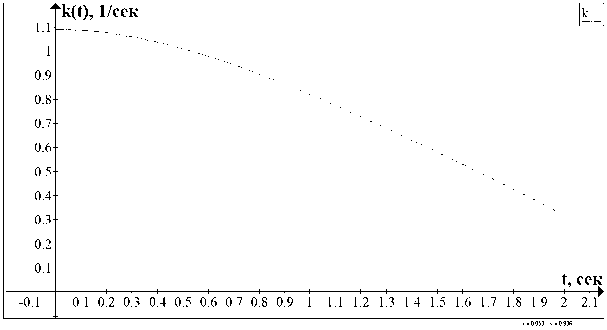
Рис. 1. Функция памяти.

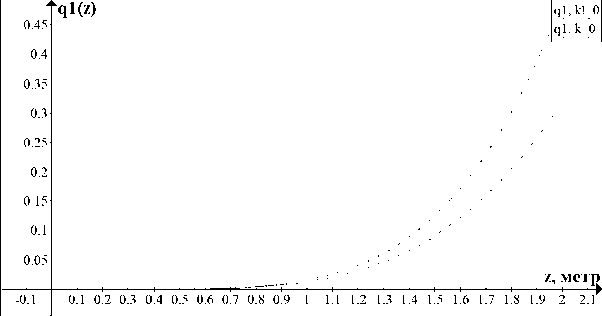
Рис. 2. Коэффициент.