Квазигармонические автоколебания в дискретном времени: анализ и синтез динамических систем
Автор: Зайцев В.В., Карлов А.В.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 4 т.24, 2021 года.
Бесплатный доступ
Для дискретизации времени в дифференциальном уравнении движения осциллятора (генератора) томсоновского типа предложено использовать сочетание численного метода конечных разностей и асимптотического метода медленно меняющихся амплитуд. Разностные аппроксимации временных производных выбираются таким образом, чтобы, во-первых, сохранить в дискретном времени консервативность и собственную частоту линейного контура автоколебательной системы. Во-вторых, требуется совпадение разностного укороченного уравнения для комплексной амплитуды автоколебаний в дискретном времени с аппроксимацией Эйлера укороченного уравнения для амплитуды автоколебаний в аналоговой системе-прототипе. Показано, что реализация такого подхода позволяет сформировать дискретные отображения осцилляторов томсоновского типа, в частности, осциллятора ван дер Поля. Адекватность дискретных моделей аналоговым прототипам подтверждена также численным экспериментом.
Автоколебательная система, уравнение движения, дискретное время, конечные разности, медленно меняющиеся амплитуды, укороченные уравнения, дискретные отображения томсоновских автогенераторов
Короткий адрес: https://sciup.org/140290771
IDR: 140290771 | УДК: 517.93 | DOI: 10.18469/1810-3189.2021.24.4.19-24
Текст научной статьи Квазигармонические автоколебания в дискретном времени: анализ и синтез динамических систем
Автоколебания – фундаментальный процесс, наблюдаемый в природе [1–3]. Среди множества разнообразных временных форм можно выделить квазигармонические (узкополосные) автоколебания. Порождающие их динамические системы – автоколебательные системы – в большинстве случаев содержат резонатор, нелинейный активный элемент и положительную обратную связь. Автоколебательная система на основе высокодобротного резонатора и активного элемента с кубической нелинейностью – генератор (осциллятор) ван дер Поля – служит универсальной моделью систем различной физической природы [4; 5]. Нелинейности более общего вида образуют класс так называемых систем томсоновского типа [6]. С учетом того, что современная теория колебаний рассматривает эволюцию динамических систем как в непрерывном (НВ), так и в дискретном времени (ДВ), представляет интерес временная дискретизация в дифференциальной модели осциллятора, результатом которой является разностное уравнение движения.
Переход к дискретному времени в дифференциальных моделях линейных аналоговых фильтров широко применяется в практике проектирования цифровых фильтров [7]. Помимо решения прикладных задач, такой подход позволяет ввести в рассмотрение колебательные ДВ-системы как объекты исследования теории колебаний. Применяемая процедура дискретизации времени накладывает свой отпечаток на характеристики порождаемой ДВ-системы. Поэтому один и тот же аналоговый прототип отображается во множество объектов динамики в дискретном времени. Это утверждение, справедливое для линейных систем, тем более относится к автоколебательным системам.
Один из способов временной дискретизации использует введение нелинейных дельта-воздействий в гамильтониан или уравнение движения НВ-системы. Например, в монографии [8] этим способом построено универсальное и стандартное отображения. В статье [9] анализ дельта-импульсной синхронизация применяется для вывода дискретных отображений неавтономного осциллятора ван дер Поля – Дюффинга. В работе [10] для проектирования ДВ-осциллятора ван дер Поля было предложено использовать условие инвариантности импульсной характеристики линейного резонатора автоколебательной системы относительно дискретизации времени. Принцип импульсной инвариантности можно сформулировать также как замену ядра интегрального уравнения движения нелинейного осциллятора дискретизирующей последовательностью дельтафункций с весовыми коэффициентами из отсчетов импульсной характеристики линейного аналогового контура.
Более традиционные способы основаны на конечно-разностных аппроксимациях временных производных в дифференциальных моделях динамических систем. Например, в статье [11] и монографии [12] дискретизация проведена методом Эйлера. Отмечено, что полученные таким образом дискретные отображения не только наследуют основные черты аналоговых прототипов, но и приобретают новые свойства. Возможности метода конечных разностей для проектирования ДВ-осцилляторов томсоновского типа проанализированы в работе [13].
В настоящей статье дискретизацию времени в дифференциальной модели генератора томсоновского типа предлагается провести на основе совместного использования методов конечных разностей и медленно меняющихся амплитуд.
1. Осциллятор в непрерывном времени
Осциллятор томсоновского типа – базовая модель теории нелинейных колебаний – задается уравнением движения вида d 2 x 2 to dx
+«0 x =- ( pS ( x - 1)m
Здесь to o и Q - собственная частота и добротность линейного резонатора; S ( x ) - дифференциальная крутизна вольт-амперной характеристики активного элемента; p – параметр превышения порога генерации (порог: p = 1). Предполагая в дальнейшем дискретизацию времени с интервалом А , введем в уравнение (1) безразмерную временную переменную т = t / А : d 2 x dx
---+ 4 п 2 qQ x = 2 nv ( pS ( x ) - 1)—. (2) d т 2 d т
Здесь Qq = to g / to d - собственная частота, измеряемая в единицах частоты дискретизации to d = 2 п / А ; v = Qq / Q - полоса резонатора.
Считая, что v << 1, анализ уравнения (2) проведем в приближении метода медленно меняющихся амплитуд (метода ММА), широко используемого при решении прикладных задач теории нелинейных колебаний [14]. В рамках метода осцилляции x(t) представляются в виде x (т) = 1 A(т)ехр( j 2nQ0 т) +1 A*(т)exp( - j 2nQ0 т) (3) с комплексной амплитудой А(т) - медленной по сравнению с ехр(j2kQqт) функцией времени. Медленность комплексной амплитуды позволяет пренебречь второй производной A"(т) в левой части уравнения (2) и первой производной A'(т) в его правой части.
Дифференциальную крутизну S ( x ) с осциллирующим аргументом (3) представим ограниченным рядом Фурье, содержащим постоянную составляющую и две первые гармоники:
S ( x ) = S q ( a ) + — S 1 ( a )exp( j 2 лQ o т ) +
+ — S 2 (a) ехр( j 4nQg т), где a =| A | - амплитуда осцилляций. После выделения первой гармоники осцилляций (3) из правой части уравнения (2) и приравнивания амплитудных коэффициентов при ехр(j2kQqт) в его правой и левой частях получим так называемое укорочен- ное уравнение вида
— = -nv I 1 - p I S o ( a ) - - S 2 ( a ) II A . d т I I 0 2 2 J J
На дискретной временной сетке т n = n Ат с шагом Ат = 1 явный метод Эйлера дает разностную форму укороченного уравнения (4):
1„
A n = A n - 1 -nvl 1 - p I S 0 ( a n - 1 ) - 2 S 2 ( a n - 1 ) I I A n -V (5)
Здесь A n = A ( т n ) - функция дискретного времени.
2. Осциллятор в дискретном времени
При переходе к дискретному времени в уравнении (2) будем стремиться выполнить два условия. Во-первых, разностный оператор второго порядка, соответствующий левой части уравнения (2), должен быть консервативным и порождать собственные колебания с частотой Qq . Это условие приводит к уравнению собственных колебаний в дискретном времени xn - 2k1 xn-1 + k2xn-2 = 0, (6) в котором действительные коэффициенты разностной аппроксимации k1 и k2 таковы, что xn = A0 ехр (j2nQ0n ) = A0Z0 .
Записав для однородного разностного уравнения (6) характеристическое уравнение
Z 0 - 2 k 1 Z 0 + k 2 = 0, нетрудно получить Z q|2 = 1 = k 2 = cos ( 2 kQq ) = k 1 .
и Ке ( Z o ) =
Теперь полное уравнение движения ДВ-осцил-лятора представим в виде xn - 2 cos(2nQo )xn-1 + xn-2 =
= 2 nv ( pS ( x n - 1 ) - 1 ) ( k з x n - 1 - x n - 2 ) .
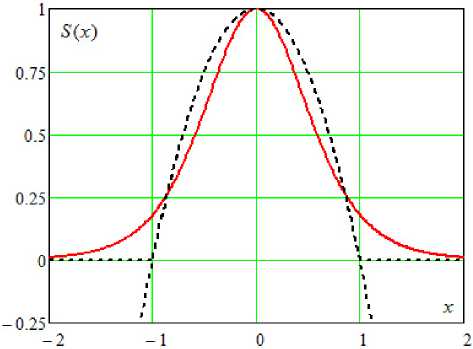
Рис.1. Дифференциальная крутизна активного элемента Fig. 1. Active element differential slope
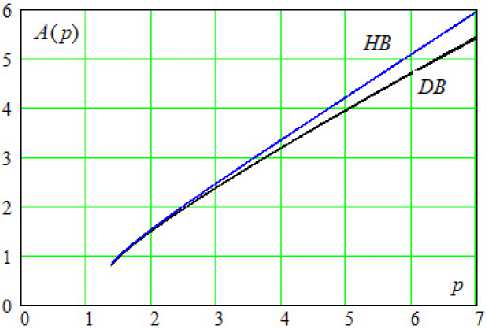
Рис. 2. Огибающие автоколебаний НВ- и ДВ-осцилляторов
Fig. 2. Amplitudes of self-oscillations in continuous and discrete time
При этом для определения коэффициента k 3 разностной аппроксимации производной в правой части (2) потребуем, чтобы укороченное уравнение для комплексной амплитуды автоколебаний в ДВ-генераторе (7) совпадало с эйлеровым приближением (5) укороченного уравнения (4) для комплексной амплитуды автоколебаний в НВ-генераторе (2).
Метод ММА на автоколебания в дискретном времени распространен в статье [15]. Следуя этой работе, автоколебания в (7) запишем в виде v - 1 A nn +1 A* 7nn xn = 2 AnZ0 + 2 AnZ0 •
Теперь медленность комплексной амплитуды An позволяет проводить преобразования левой части уравнения (7) с учетом приближенного равенства A n - A n - 1 = A n - 1 - A n 2 , а в его правой части считать комплексную амплитуду постоянной. Все остальные шаги ДВ-метода ММА совпадают с аналогичными шагами НВ-метода. В результате приходим к следующему укороченному уравнению для ДВ-осциллятора (7):
( k 3 - Z 01 )
An = An -1 — nv ---7—v x jIm (Z 0) (8)
L C , 1 „, x))
x I 1 - p I S 0 ( a n - 1 ) - 2 S 2 ( a n - 1 ) I I A n - 1 •
Нетрудно увидеть, что уравнение (8) совпадает с уравнением (5), если положить к3 = Re (Z0 ) = = cos(2kQo )• Таким образом, искомое дискретное отображение (разностное уравнение движения), определяющее ДВ-осциллятор ван дер Поля, имеет вид xn - 2 cos(2nQ0 )xn-1 + xn-2 =
= 2 nv ( pS ( x n - 1 ) - 1 ) ( cos ( 2 лПо ) x n - 1 - x n - 2 ) •
При умеренных превышениях порога генерации ( p < 10), когда автоколебания еще можно считать квазигармоническими, отображение (9) воспроизводит в дискретном времени основные характеристики НВ-осциллятора (1). Этот вывод непосредственно следует из способа его формирования. Тем не менее приведем также ряд результатов цифрового анализа временных рядов, генерируемых по алгоритму (9).
3. Численный эксперимент с томсоновским ДВ-осциллятором
В качестве примера рассмотрим автоколебания в ДВ-осцилляторе (9) с нелинейностью дифференциальной крутизны вида
( 3 )
S ( x ) = 1 - th2 I — x I .
График функции (10) приведен на рис. 1. Для сравнения пунктирной линией показаны графики квадратичной нелинейности дифференциальной крутизны
S ( x ) = 1 - x 2, соответствующей осциллятору ван дер Поля, и ограниченной квадратичной нелинейности.
Энергетические характеристики НВ- и ДВ-осцилляторов можно сопоставить путем сравнения зависимостей амплитуд Ac и Ad первой гармоники установившихся автоколебаний от величины параметра превышения порога генерации. Соотношение этих зависимостей иллюстрируют графики, приведенные на рис. 2.
Для дискретного осциллятора (9) с параметрами Qo = 0,18, Q = 20, v= 9 ■ 10 - 3 график зависимости A d ( p ) получен путем оценки амплитуды автоколебаний по формуле
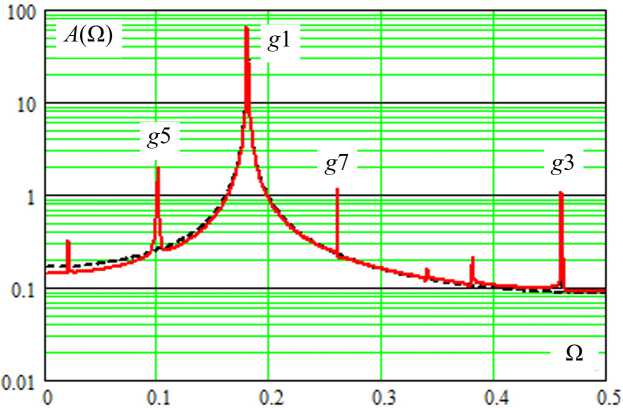
Рис. 3. Амплитудные спектры НВ- и ДВ-осцилляторов
Fig. 3. Amplitude spectrum of CT- and DT-oscillators
A d ( p ) =1 xN ( p ) +
cos ( 2 nO 0 ) x N ( p ) - x N - 1 ( p ) sin ( 2 nQ o )
на основе отсчетов Xn-1 и Xn временного ряда. Отметим, что при записи (10) использована ап проксимация производной y = dy / dт вида [15]
sinc (2л°0 ) yn = (cos (2kQo ) xn - xn-1), где sinc(2nQo ) = sin(2nQo) / 2nQo - кардинальный синус.
Оценка амплитуды Ac(p) установившихся автоколебаний томсоновского осциллятора (1) прове- дена на основе результатов численного интегрирования задачи Коши для уравнения движения (2) методом Рунге – Кутта четвертого порядка с фиксированным шагом Дт = 0,125. Временные ряды для оценки Ac (p) сформированы путем выборки из численного решения Xn = xnM, Yn = Упм = = xт (тnM) при M = 8, а затем использована формула Ac(p) = XN (p) + [ ^ ] .
V ( 2 пО 0 )
В целом, как это следует из рис. 2, зависимости Ac (p) и Ad (p) близки как качественно, так и количественно – максимальное расхождение их значений в представленном примере составляет 8,4 %. Причем причина замедленного роста Ad (p) по сравнению с Ac (p) при увеличении параметра p заключается в повышенном уровне гармоник у ДВ-осциллятора (9). Это подтверждается рис. 3, на котором для p = 3 сплошной линией показан амплитудный спектр автоколебаний ДВ-осциллятора (9), а пунктирной – НВ-осциллятора (1). Символами gK отмечены гармоники с номерами K. Здесь следует обратить внимание на неустранимый эффект подмены частот (наложения спектров) гармоник автоколебаний в дискретном времени [16]. Что ка- сается основных частот автоколебаний, то они в представленном примере у осцилляторов (1) и (9) весьма близки.
4. Разновидности ДВ-осцилляторов томсоновского типа
Основываясь на дискретном отображении (уравнении движения) осциллятора ван дер Поля, можно предложить еще ряд ДВ-автогенераторов томсоновского типа.
Вариант уравнения движения (9) нетрудно получить, если ввести в рассмотрение параметр консервативности резонатора ДВ-автогенератора: 5 = 1 - nv ^ exp( -nv ).
Тогда (9) принимает вид
-
xn - 2 5 cos ( 2 пО 0 ) xn - 1 +5 2 xn - 2 =
= 2 nv pS ( xn - 1 ) ( cos ( 2 KQ o ) xn - 1 - xn - 2
Очевидно, что при 5 = 1 и S(x) = 1 - x2 разност- ное уравнение
-
xn - 2 cos ( 2 nQ o ) xn - 1 + xn - 2 =
= 2nvp(1 - хП-1 )(cos(2nQo ) xn-1 - xn-2 ), представляет собой результат дискретизации времени в уравнении ван дер Поля в его стандартной форме записи [4]:
d 2 x 22 dx
— + toox = «oY(1-x )-, где у = pQ - константа глубины обратной связи.
Вариант ДВ-автогенератора с перестройкой частоты задается уравнением
-
xn - 2 cos ( 2 nQ 0 ( 1 + m n ) ) xn - 1 + xn - 2 =
= 2nv (pS (xn-1) - 1) (cos (2KQ0 ) xn-1 - xn-2 ), где mn = ДОn / Q0 - текущее значение индекса частотной модуляции; ДОn - девиация частоты.
Заключение
Предложенный метод дискретизации времени в дифференциальном уравнении квазигармони-ческой автоколебательной системы (системы томсоновского типа) позволяет перейти к рассмотрению дискретных отображений, гарантированно обладающих динамическими характеристиками аналоговых систем-прототипов. Такие отображения можно использовать в качестве нелинейных функциональных узлов в численных моделях сложных радиоэлектронных устройств. Кроме того, они могут служить основой алгоритмов об- работки дискретных (цифровых) сигналов, таких, например, как синхронное и частотное детектирование [17].
При значительных превышениях порога генерации, когда перестает выполняться условие квази- линейности исходной автоколебательной системы, дискретные отображения приобретают новые свойства, позволяющие рассматривать их как самостоятельные объекты нелинейной динамики в дискретном времени.
Список литературы Квазигармонические автоколебания в дискретном времени: анализ и синтез динамических систем
- Андронов А.А., Витт А.А., Хайкин С.Э. Теория автоколебаний. М.: Наука, 1981. 508 с.
- Мюррей Дж. Математическая биология. Т. I. Введение. М.; Ижевск: НИЦ РХД, Институт компьютерных исследований, 2009. 776 с.
- Jenkins A. Self-oscillations // Physics Reports. 2013. Vol. 525, no. 2. P. 167–222. DOI: https://doi.org/10.1016/j.physrep.2012.10.007
- Кузнецов А.П., Кузнецов С.П., Рыскин Н.М. Нелинейные колебания. М.: Физматлит, 2005. 292 с.
- Феномен уравнения ван дер Поля / А.П. Кузнецов [и др.] // Известия вузов. Прикладная нелинейная динамика. 2014. Т. 22, № 4. С. 3–42. DOI: https://doi.org/10.18500/0869-6632-2014-22-4-3-42
- Основы теории колебаний. Изд. 2-е / В.В. Мигулин [и др.]. М.: Наука, 1988. 392 с
- Оппенгейм А., Шафер Р. Цифровая обработка сигналов. М.: Техносфера, 2006. 856 с.
- Заславский Г.М. Гамильтонов хаос и фрактальная динамика. М.; Ижевск: НИЦ РХД; Ижевский институт компьютерных исследований, 2010. 472 с.
- Кузнецов А.П., Тюрюкина Л.В. Синхронизация автоколебательной системы Ван дер Поля – Дуффинга короткими импульсами // Известия вузов. Прикладная нелинейная динамика. 2004. Т. 12, № 5. C. 16–31.
- Зайцев В.В., Давыденко С.В, Зайцев О.В. Динамика автоколебаний дискретного осциллятора ван дер Поля // Физика волновых процессов и радиотехнические системы. 2000. Т. 3, № 2. С. 64–67.
- Кузнецов А.П., Савин А.В., Седова Ю.В. Бифуркация Богданова – Такенса: от непрерывной к дискретной модели // Известия вузов. Прикладная нелинейная динамика. 2009. Т. 17, № 6. С. 139–158.
- Морозов А.Д. Резонансы, циклы и хаос в квазиконсервативных системах. М.; Ижевск: НИЦ РХД; Ижевский институт компьютерных исследований, 2005. 424 с.
- Зайцев В.В., Федюнин Э.Ю., Шилин А.Н. Конечные разности в задаче синтеза нелинейных ДВ-осцилляторов // Физика волновых процессов и радиотехнические системы. 2017. Т. 20, № 2. С. 35–41. URL: https://journals.ssau.ru/pwp/article/view/7095
- Капранов М.В., Кулешов В.Н., Уткин Г.М. Теория колебаний в радиотехнике. М.: Наука, 1984. 320 с.
- Зайцев В.В. О дискретных отображениях осциллятора ван дер Поля // Физика волновых процессов и радиотехнические системы. 2014. Т. 17, № 1. С. 35–40. URL: https://journals.ssau.ru/pwp/article/view/7287
- Зайцев В.В., Стулов И.В. О влиянии подмененных гармоник на динамику автоколебаний в дискретном времени // Известия вузов. Прикладная нелинейная динамика. 2015. Т. 23, № 6. С. 40–46. DOI: https://doi.org/10.18500/0869-6632-2015-23-6-40-46
- Линдсей В. Системы синхронизации в связи и управлении. М.: Мир, 1972. 600 с.


