Квазиоптимальное обнаружение сверхширокополосного сигнала при воздействии узкополосной помехи

В последнее время значительное внимание уделяется применению сверхширокополосных сигналов (СШПС) в радиолокации, радионавигации, связи и т. п. Об этом свидетельствует множество научных работ опубликованных за последние десятилетия, в том числе и [1–4]. Использование СШПС имеет свою специфику и позволяет в принципе значительно расширить информационные возможности радиосистем.

Физическая основа целесообразности использования СШПС достаточно очевидна – количество информации, передаваемой в единицу времени, прямо пропорционально полосе используемых частот. Альтернативой этому могло бы являться увеличение времени передачи информации, но время функционирования радиосредств, например, военного назначения всегда ограничено, поэтому проблема повышения информативности при использовании традиционных подходов остается.

В развитых иностранных государствах СШП-технологии все более широкое применение находят в военной и специальной технике. В связи с этим возникает необходимость в радиоэлектронной разведке сигналов таких радиосредств. Для повышения эффективности разведки СШП-сис-тем предлагается синтезировать алгоритм функционирования перспективных средств обнаружения СШПС. Учитывается, что прием СШПС осуществляется в условиях, приближенных к реальным, то есть в процессе обнаружения могут осуществляться воздействия как преднамеренных помех в виде, например, гауссовских узкополосных помех (ГУП), так и непреднамеренных помех в виде гауссовского белого шума (ГБШ) [6], кроме того, могут быть неизвестны некоторые параметры сигналов и помех.

Вследствие априорной неопределенности характеристик сигналов и помех операция обнаружения в процессе разведки связана с дополнительными потерями, которые влияют на ее эффективность.

Цель работы: определить структуру и характеристики обнаружителя СШПС неизвестной формы на фоне белого шума при воздействии преднамеренных помех с неизвестной формой функции корреляции.

Конкретизируем общие положения теории обнаружения применительно к сверхширокополосным сигналам.

Пусть на интервале времени t е [0; T ] наблюдается реализация при наличии сигнала вида

x ( t ) = s ( t ) + n ( t ) + £( t ), (гипотеза Н ), (1)

а при его отсутствии

x ( t ) = n ( t ) + £( t ), (гипотеза H_Q ). (2) Здесь n ( t ) – ГБШ с односторонней спектральной плотностью N _o; £( t ) — центрированная ГУП, которая имеет априори неизвестную корреляционную функцию B ^ ( 1 2 - t i ); s ( t ) — полезный сигнал, форма которого также априори неизвестна.

В статье предлагается выполнить синтез оптимального алгоритма обнаружения для предполагаемых (ожидаемых) сигнала s ₁( t ) и помехи с функцией корреляции B^ ( 1 2 - t i ). Такой обнаружитель формирует величину вида

T

L = J x ( t ) P i ( t ) dt . (3) 0

Решение о наличии сигнала принимается, если L > h , и об отсутствии, если L < h . Здесь h — порог обнаружения сигнала. Функция v ₁( t ) определяется из решения интегрального уравнения

T

N о ^у 1 ( t ) /2 + J B 1 ^ ( t — т) V 1 (т) d т = S 1 ( t ).

Поскольку L (3) является гауссовской случайной величиной, для вероятностей ошибки

TT

= JJ “2 ° 8 ⁽ t 1 ^— t 2 ) ⁺ B ⁽ t 1 0 0 ^L

—

t 2 ) ^x

T

N x v1(t1)v1(12)dt1 dt2 = —0 I v2(t)dt +

1-го рода (ложной тревоги) а и ошибки 2-го (пропуска сигнала) в можно записать [6; 7]

рода

а = P ( L >  hH₀) = 1 — Ф

h — m 0 1

^ 0 ),

в = P ( L <  h\H 1 ) = Ф

h — m ₁

^ 1

.

Здесь

x

Ф( x ) =       exp

V 2n

—

^{2 2}1 — I dt

2 )

—да

– интеграл вероятности, а

mi

= <  LH i > ,  с² =< ( L — m i )²|

H i > ,

–

математическое ожидание и дисперсия

слу-

чайной величины (3), когда верна гипотеза H_i ( i = 0,1). Воспользовавшись для определенности критерием Неймана – Пирсона [5], найдем из (4) значение порога

h = m о + ^ o arc Ф(1 — а),

который обеспечивает уровень ложных тревог а. Здесь arc Ф( x ) — функция, обратная интегралу вероятности Ф( x ). Подставляя (7) в (5), получаем для вероятности пропуска сигнала выражение

в = Ф ^ 0- arc Ф(1 — а) — Z 1 ,

L ^G 1

где

2    ( m 1 — m 0 )²

^z 1 =------- 2       ,

° 2

–

отношение сигнал – шум (ОСШ) по мощности

на выходе обнаружителя (3).

Для того чтобы найти характеристики обнаружения (4) и (5), достаточно определить моменты (6) случайной величины (3).

Подставляя (2) в случае отсутствия сигнала в (6), получаем

J T m0 = 0, ^2 = < ^ f [n(t) + ^(t)]v1(t)dt >

1 0                              J

>=

TT

+ J J B ^ ⁽ t 1 ^— t 2^{) v} 1⁽ t 1^{) v} 1⁽ t 2 ) ^dt 1 ^dt 2 .

Далее аналогично при наличии сигнала (1) находим

T

m 1 = J s ( t )v 1 ( t ) dt , G 2 = o 0 .

Подставляя затем (9) и (10) в (8), получаем для выходного ОСШ выражение

z ₁ 2 =

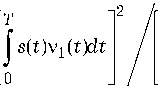
v 2 ( t dt +

TT

⁺ J J B ^ ⁽ t 1 ^— t 2^{) v} 1⁽ t 1^{) v} 1⁽ t 2 ) ^dt1^dt 2 .

0 0                                           _

Полагая, что форма ожидаемого ла совпадает с формой принимаемого,

сигна-

то есть

s ₁( t ) = s ( t ) и формы корреляционных функций принимаемой и ожидаемой помех также совпадают, то есть при B 1 ^ ( 1 2 — t 1 ) = B ^ ( 1 2 — t 1 ) получаем из (11) ОСШ для оптимального обнаружителя [6]

T

z 2 = J s ( t )v( t)dt ,

где v( t ) определяется из решения интегрального уравнения

T

N o v ( t ) /2 + J B ( t — т) v (т) d т = s ( t ).

Найдем параметры, определяющие изменение

эффективности чия априорной ренных помех.

Проигрыш в

обнаружения вследствие нали-неопределенности и преднаме-

ОСШ вследствие отклонения

ожидаемой формы сигнала и корреляционной функции помехи от истинных можно получить, используя (11) и (12)

^Х 1    ^z0 / ^z 1 ,

также этот параметр учитывает сам факт наличия ГУП.

Рассмотрим полученный показатель эффективности (13) в спектральном представлении.

Для этого, используя преобразование Фурье и теорему Винера – Хинчина, запишем спектры сигналов (принимаемых и ожидаемых; для случая оптимального обнаружения на фоне только ГБШ и для оптимального приемника всей реализации (1)): да

S ( j to) = J s ( t )exp(- j to t ) dt ,

-да

Ю

S 1 ( j to) = J s i ( t)exp(-j to t ) dt ,

-да да

S ( j to)

V ( j to) = v ( t )exp(- j to t ) dt =                  ,

N 0 /2 + G _| ( to ) -да да

Х 1 =

x

V 1 ( j «» = J v 1 ( t )exp( ^- j _ш t ) dt =

-да

S 1 ( j to)

N ° / 2 + G 1 | ( ^to )

а также представим спектры мощности помехи (принимаемой и ожидаемой) в виде да

G । (to) = J B ^ (т)ехр(- j toT) d т

-да да

G 1 | (to) = J B i ^ (т)ехр(- j toT) d т.

-да

В этом случае проигрыш (13) запишется как

= да      ।s ( j to)²      d

^{X 1 J} N 0 /2 + G _| (to)^dC°^X

_x ^да | S i ( j to)² [ N ° /2 + G । (to)] d _to

-да ^{[ N} ° /2 ^{+ G} 1 | ^{( to )]}         ,

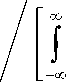
S ( j to) S * ( j to) N 0 / ² + G 1 | ^{( to )}

d to

Обозначив в этом выражении P | (to) = 2 G । (to) / N ° , P 1 | (to) = 2 G ^(to) / N о, получим

да

Z 1 = J

-да

| S ( j to)^

1 + P | (to)

d to x

_x ^да S 1 ( j to),^{2 [} 1+p ^ (to)] d _to

-да ^{[ 1 + p} 1 ^ ^{( to )} ]           ,

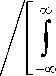
S ( j to) S * ( j to) 1 + P 1 | (to)

d to

Если форма сигнала известна, то есть

S 1 ( j to) = S ( j to), то проигрыш вследствие воздействия помех с неизвестной формой спектра мощности ( G 1 ( j to) * G ( j to)), согласно (14), примет вид

^да | S ( j to)^{2 J} 1 + P | (to)

-да

I S ( j to)|² [1 + P | (to)]

^[ 1 + P 1 | (to)]²

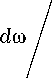
да J -да

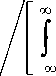
| S ( j to)|²

1 + P 1 | (to)

d to

Проигрыш при наличии помех известной формы ( G 1 ( j to) = G ( j to)) вследствие наличия априорной неопределенности о форме принимаемого сигнала ( S 1 ( j to) * S ( j to)), используя (14), определим как

да

^Х '1 = J

-да

| S ( j to)^

1 + P | (to)

d to x

x

I ^Sj\ d J ^[ 1 + P ^ (to)] j

да J -да

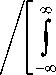
S ( j to) S * ( j to) 1 + P ^ (to)

d to

Проигрыш вследствие наличия помех известной формы ( G 1 ( j to) = G ( j to)) и при совпадении форм принимаемого и ожидаемого сигналов ( S 1 ( j to) = S ( j to)) запишется как % ! = 1, то есть проигрыш отсутствует.

В качестве конкретного примера рассмотрим

узкополосную помеху с прямоугольным спектром мощности, наблюдаемую на входе обнаружителя

„ . . Y т Г ton - оэ^ _ (ton + оэ^

G= (to) = ^Y I -°---- + 1 -°---- ,

^       2 L I Q ) I Q J_

где to ° — центральная частота;

да

Q=j

G | (to) d to / max G 2 (to) ш

— эквивалентная полоса частот; у — спектральная плотность ГУП, а f1, к |< 1/2

I ( x ) = ] ,                .

[°,| x |> 1/2

Помеху, на которую настроен приемник, представим следующим спектром мощности:

^G 1 | ^{( to )} = Yr

1 1 to ° - to [ Q

। to + to

+ 1   °----

I Q

Предполагаем, что полосы и частоты принимаемой и ожидаемой помех совпадают, а различаются только по интенсивности у * Y 1 - Обозначим q = у / N ° , q 1 = У 1 / N ° — отношение интенсивности помех и шума и

to ₀ +□ /2

f

Oo-Q /2

S =------- да

I S ( j to)² d to

f S ( j to)| 2 d to 0

– относительная доля энергии СШПС в полосе частот, пораженной помехой.

Проигрыш в ОСШ вследствие отличия интенсивностей помех с одинаковой формой спектра мощности и при совпадении форм принимаемого и ожидаемого сигналов запишется, согласно (14), как

X =

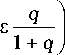
1 + _S ^q - ^{2 q} 1 - ^q1

. (i + q i )²   .

1 - -^_ _e ]

^{1 +} q i J

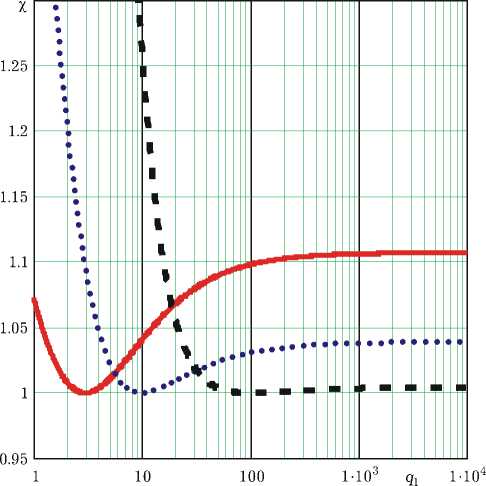
Рис. 1

Рассмотрим предельные случаи проигрыша (15).

При наличии на входе приемника, синтезированного для приема сигнала на фоне только

ГБШ ( q 1 = 0), помехи с интенсивностью q возникает снижение ОСШ на выходе обнаружителя,

определяемое как

X =

-

^S q

¹ + q

(1 + Sq ).

В случае, когда q 1 ^ да, то есть приемник настроен на помеху с бесконечной интенсивностью, а принимается помеха с конечной интенсивностью, проигрыш будет X = [ 1+ q (1 -б)]/ (1 — б)(1 + q ). В этом случае рассматриваемый квазиоптималь-ный обнаружитель будет соответствовать обнаружителю, оптимальному для приема СШПС на фоне только ГБШ с режекторным фильтром на входе, вырезающим помеху. В случае совпадения интенсивностей принимаемой и ожидаемой помех ( q 1 = q ) проигрыш отсутствует — X = 1.

На рисунке представлены зависимости проигрыша (15) от интенсивности ожидаемой помехи (на которую настроен приемник) для значения б = 0,3 при различных интенсивностях принимаемой помехи — q = 5 (сплошная кривая), 10 (пунктирная), 100 (штриховая).

Анализ полученных зависимостей показывает, что в случае, когда интенсивности ожидаемой и принимаемой помех совпадают, то есть q 1 = q , проигрыш отсутствует (формула (15)). При этом если q 1 >  q , то проигрыш с увеличением q ₁ (интенсивности ожидаемой помехи) растет гораздо медленнее, чем при q 1 <  q . Таким образом, если точно интенсивность принимаемой

помехи неизвестна, то можно выбирать ее значение с некоторым запасом, то есть использовать приемник, настроенный на помеху с большей интенсивностью, чем принимаемая. В этом случае попадем на участок кривой (см. рис.), где проигрыш растет медленнее и, соответственно, эффективность обнаружения выше. Также графики подтверждают рассмотренные предельные случаи проигрыша (15).

Полученные результаты позволяют сделать обоснованный выбор структуры обнаружителя в зависимости от имеющейся априорной и получаемой в процессе разведки информации о параметрах преднамеренной помехи, а также в зависимости от требований, предъявляемых к эффективности аппаратуры обнаружения СШП-излучений.