Квазистатическое и электродинамическое моделирование модальных явлений в многопроводных структурах

Изучение процессов распространения импульсных сигналов в многопроводных структурах представляет практический интерес [1]. В работе [2] рассмотрены модальные искажения импульса. Однако для более глубокого их изучения и применения на практике необходимо тщательное моделирование. Для этого применяются системы электродинамического и квазистатического моделирования. Причиной тому являются развитие методов моделирования, вычислительной техники, определенные преимущества моделирования над экспериментом. Каждый из подходов моделирования имеет свои сильные и слабые стороны и оптимальные области применения. Например, электродинамика на основе уравнений Максвелла учитывает все происходящие волновые процессы, требуя больше вычислительных ресурсов относительно квазистатики. Описание процессов в квазистатике основано на телеграфных уравнениях, с учетом допущений и ограничений применения. К сожалению, пользователи систем моделирования не всегда это учитывают и часто работают лишь с одной системой, не соотнося методологию моделирования со спецификой задачи. Ряд результатов моделирования [3] показывает, что такой подход может быть неэффективным.

Цель данной работы – обобщить известные и представить новые результаты моделирования модальных явлений в многопроводных структурах, показывающие важность гибкого подхода при выполнении моделирования.

Модальные искажения импульса проявляются в том, что при его распространении в многопроводной структуре с неоднородным диэлектрическим заполнением из N проводников (не считая опорного) может меняться форма импульса, вплоть до разложения на N импульсов меньшей амплитуды из-за различия погонных задержек мод в линии. В этой работе рассматриваются структуры с разностью задержек мод, позволяющей наблюдать подобного рода искажения.

Эти структуры имеют относительно большое отношение длины структуры (1…1,25 м) к ширине (≈4 мм). Поэтому волновые процессы в них (пока длина волны много больше ширины структуры) можно рассматривать, пользуясь теорией линий передачи. Стоит отметить, что поверхностные методы моделирования аппроксимируют только поверхности структуры. Объемные методы аппроксимируют объем структуры и определенное пространство вокруг нее, и поэтому для узкой и длинной структуры применение данных методов не очень эффективно. Приведенные ниже результаты моделирования подтверждают это.

Рис. 1. Поперечное сечение структуры 1, где проводники: А – активный, О – опорный, П – пассивный

Моделирование проводилось в системах TALGAT (квазистатический анализ) и CST MWS (электродинамический анализ). Значение параметров сегментации в TALGAT выбрано такое, что дальнейшее ее учащение не влияет на результаты моделирования. В CST MWS были выбраны два набора параметров сегментации: «редкая» и «частая». Частая сегментация ограничивалась вычислительными возможностями рабочей станции. Два набора сегментации выбрано с той целью, чтобы можно было оценить, будут ли результаты электродинамики приближаться к результатам квазистатики при учащении сегментации.

В качестве первой структуры выбрана связанная линия из трех проводников на диэ-

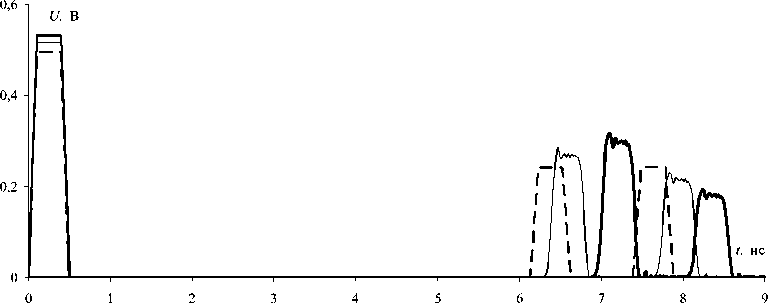
Рис. 2. Формы сигналов в начале и конце активного проводника структуры 1, полученные при редкой ( – ) и частой (––) сегментациях в CST MWS и в TALGAT (- - -)

лектрической подложке. В данной структуре распространяются четная и нечетная моды, а геометрические параметры подобраны так, чтобы получить максимальную разность задержек мод [4], составившую ≈1,25 нС. Трапециевидный сигнал с ЭДС 1 В и длительностью фронтов 100 пС и плоской вершины 300 пС подавался между опорным и активным проводниками структуры длиной 1,25 м (см. рис. 1) с параметрами поперечного сечения: h = 0,29 мм; t = 0,105 мм; w = 0,3 мм; s = 0,4 мм; εr = 5. Сопротивления между опорным и активным, а также опорным и пассивным проводниками на обоих концах равны 100 Ом. Вычисления проводились без учета потерь.

Результаты моделирования приведены на рис. 2, а их параметры сведены в таблицу 1. Время вычисления TALGAT составило 11 С, а CST MWS – 2 ч 7 мин. (редкая сегментация) и 6 ч 33 мин. (частая сегментация). При увеличении сегментации в CST MWS наблюдается сходимость результатов CST MWS к результатам TALGAT: по амплитудам импульсов в начале и конце линии, по времени

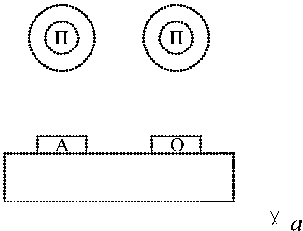
Рис. 3. Поперечное сечение (а) и схема подключения (б) структуры 2

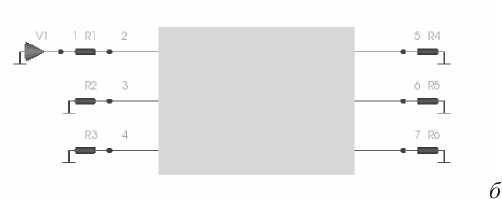
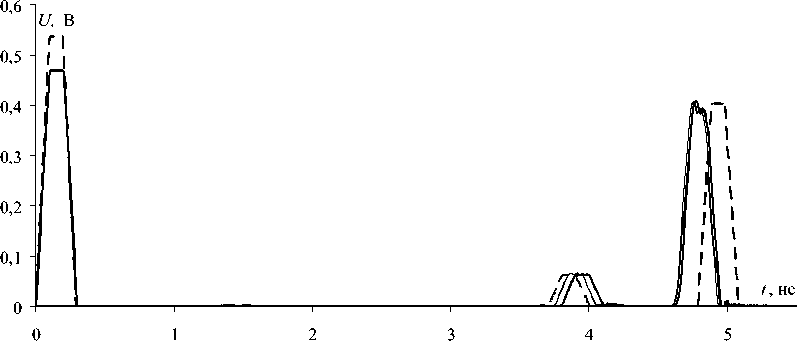
Рис. 4. Рис. 4. Формы сигналов в начале и конце активного проводника структуры 2, полученные при редкой ( – ) и частой (––) сегментациях в CST MWS и в TALGAT (- - -)

задержки в линии (см. рис. 2 и таблицу 1). Из этого следует, что для данной структуры результаты TALGAT более корректны.

Практический интерес для модального зондирования [5] представляет изучение многомодовых структур (где присутствуют более двух мод). На рис. 3 приведены поперечное сечение структуры 2 (из четырех проводников, два из которых имеют криволинейные границы) и графическое отображение подключений элементов, полученные в системе TALGAT. Параметры структуры: толщина диэлектрика 0,29 мм; толщина полосок 0,105 мм; ширина полосок 0,3 мм; расстояние между краями полосок 0,4 мм; расстояние между краями полосок и диэлектрика 0,2 мм; εr = 5; для проводов – радиус жилы 0,1 мм, толщина изоляции 0,1 мм; высота центров относительно верхнего края полосок 0,6 мм; εr = 3. Импульсный сигнал (длительность фронтов и плоской вершины 100 пС) с ЭДС 1 В подавался между активным и опорным проводниками структуры длиной 1 м с сопротивлениями на концах 100 Ом. Результаты моделирования приведены на рис. 4 и сведены в таблицу 1.

Как и в предыдущем примере, наблюдается сходимость результатов CST MWS и TALGAT. Время вычисления TALGAT составило 8 С, а CST MWS – 6 ч 48 мин. (редкая сегментация) и 11 ч 45 мин. (частая сегментация).

Рис. 5. Сегментированное поперечное сечение структуры 3 при длине сегмента 50 мкм

Для практического использования модальных явлений желательны компактные структуры довольно большой длины [4]. Поэтому актуально уменьшение габаритов структуры, например, сворачиванием в меандровую линию. Для этого нужна оценка влияния полувитков меандра посредством моделирования структур, подобных приведенной на рис. 5. Интересна и возможность моделирования с учетом потерь только в диэлектриках, поскольку избавиться от потерь в проводниках в натурном эксперименте невозможно. Между тем результаты подобного моделирования позволяют оценить, как влияют на форму сигнала потери именно в диэлектриках.

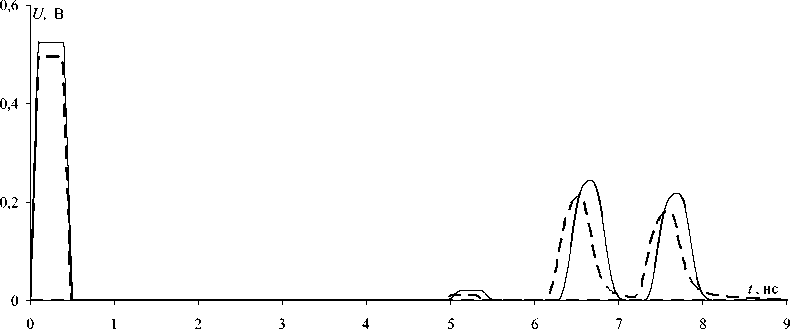
Рис. 6. Формы сигналов в начале и конце активного проводника структуры 3, полученные в CST MWS (––) и TALGAT (- - -)

Подавался трапециевидный сигнал (фронты 100 пс, плоская вершина 300 пС, ЭДС 1 В) между опорным и активным (0 и 1) проводниками структуры 3 (рис. 5), состоящей из 6 проводников длиной 1,25 м и параметрами: h = 0,29 мм; t = 0,035 мм; w = 0,3 мм; s = 0,4 мм; s1 = 1,5 мм; материал подложки – FR-4. Потери в проводниках не учитывались. Значение всех сопротив- лений равно 100 Ом. Результаты приведены на рис. 6 и сведены в таблице 1.

Время вычисления в TALGAT составило 33 мин., а в CST MWS – 8 ч 1 мин. Небольшое различие результатов (рис. 6) объяснимо разными методами, на которых основаны системы (метод моментов и метод конечного интегрирования), и различным представлением в системах о материале FR-4 и его частотной зависимости. Приведенные результаты моделирования (рис. 2; 4; 6) показывают, что в начале активной линии 1 импульс, а к концу линий приходит 2 или 3 импульса. Увеличение числа импульсов в конце линии объяснимо модальным разложением по теории многопроводных линий передачи. К концу активного проводника структуры 1 приходят 2 импульса меньшей амплитуды вместо одного, что иллюстрирует возможность применения модальных явлений для защиты от сверхкоротких импульсов в линии. В структуре 2 к концу активного проводника приходят также 2 импульса, несмотря на то, что структура четырехпроводная (N = 3) и на конце может наблюдаться 3 импульса (наличие только двух импульсов объясняется тем, что минимальная разность задержек мод для данной структуры незначительна и меньше длительности импульса, поэтому для двух мод происходит наложение импульсов). В структуре 3 (N = 5) к концу линии приходит 3, а не 5, импульсов из-за наложения импульсов с близкими задержками мод. Появление малого импульса объяснимо наличием полувитка рядом с активной линией. Отме- тим также, что результаты моделирования всех трех структур иллюстрируют возможность бесконтактного обнаружения как однопроводных (структура 1), так и многопроводных структур (структуры 2 и 3) по форме искажения импульса в активном проводнике.

Приведенные результаты показывают хорошую согласованность квазистатики и электродинамики. Затраты времени на вычисление отличаются в 15-5287 раз. Максимальная разность результатов составляет 12% по задержке и 29% по значительным амплитудам (см. таблицу 1). Стоит отметить, что при увеличении сегментации в CST MWS различие между результатами электродинамики и квазистатики сокращается (см. таблицу 1), поэтому можно утверждать, что результаты квазистатики более корректны для данных структур. Примечательным является тот факт, что при усложнении геометрии структур (увеличение числа проводников, добавление криволинейных границ раздела сред) данная тенденция сохраняется и квазистатика дает стабильные результаты. Таким образом, методология моделирования должна быть гибкой и соответствовать специфике решаемой за-

Таблица 1. Значения задержек и амплитуд импульсов (И1, И2, И3) в конце активного проводника, полученные в TALGAT и CST MWS

TALGAT Результаты CST MWS (относительная разность TALGAT и CST MWS: Щсет-Пгм смУП-гм.gat,%) Редкая сегментация Частая сегментация И1 И2 ИЗ И1 И2 из И1 И2 ИЗ Структура 1 Время задержки для каждого из импульсов, нс 6,14 7,4 - 6,9(12%) 8,1 (9 %) - 6,33 (3 %) 7,68 (4 %) - Значение амплитуд импульсов, В 0,24 0,24 - 0,3 (25 %) 0,18(25%) - 0,26 (8 %) 0,21 (13 %) - Структура 2 Время задержки для каждого из импульсов, нс 3,7 4,8 - 3,8 (3%) 4,64 (3%) - 3,75 (1%) 4,62 (3%) - Значение амплитуд импульсов, В 0,06 0,4 - 0,06 0,39 (3%) - 0,06 0,39 (3%) - Структура 3 Время задержки для каждого из импульсов, нс 4,9 6,1 7,2 - - - 5 (2%) 6,3 (3%) 7,3 (1%) Значение амплитуд импульсов, В 0,01 0,21 0,17 - - - 0,02(100%) 0,24(14%) 0,22 (29%) дачи и требованиям к точности. Гибкость подхода к моделированию сэкономит необходимые время и вычислительные ресурсы, что особенно актуально при оптимизации большого числа параметров в широком диапазоне. Результаты квазистатического моделирования позволили найти практическое применение модальным явлениям [6-8].

Работа выполнена в порядке реализации постановления №218 Правительства РФ от 09.04.2010 г. «О мерах государственной поддержки развития кооперации российских высших учебных заведений и организаций, реализующих комплексные проекты по созданию высокотехнологичного производства» и договора № 13.G25.31.0017 от 07.09.2010 между ОАО «ИСС им. акад. М.Ф. Решетнева» и Минобрнауки РФ.