Квазистатическое моделирование формообразования отверстий многолезвийными инструментами

Для повышения эффективности прогнозирования точности обработки деталей на стадии проектирования необходимо оснастить современные интеллектуальные системы CAM/CAE адекватными математическими моделями расчета погрешностей обработки. Рассмотрим, как эту проблему можно решить при моделировании процесса формообразования отверстий многолезвийными инструментами.

Наиболее полно процесс формообразования отверстий может быть описан системой дифференциальных уравнений, учитывающей наличие всех возможных перемещений и действующих сил, в том числе и инерционных [1]. Исследования этих систем показали, что для расчета точности обработки отверстий развертками и зенкерами с любым числом лезвий в математических моделях достаточно учитывать лишь радиальные составляющие сил резания (1).

JY ( t ) = - ^ Kr i h i cos v i ( S • tg V / z + X ( t ) cos V i + Y ( t ) sin V i —

i

- X ( t -τ )cos ψ _i - Y ( t -τ )sin ψ _i )/tg ϕ

-

JX ( t ) = - ^ Kr i h i sin v i ( S • tg ^ / z + X ( t )cos V i + Y ( t )sin v i

i

-X(t-τ)cosψi-Y(t-τ)sinψi)/tgϕ, где J – жесткость инструмента; X(t) и Y(t) – текущие координаты центра инструмента (рис. 1); Kri – коэффициент пропорциональности радиальных сил резания Pi площадям срезаемых слоев; hi – величина срезаемого припуска i-м лезвием; ψi – текущий угол поворота i-го лезвия; S – подача; ϕ – главный угол в плане режущей части инструмента; z – число лезвий; τ = 2π/zω (где ω – угловая скорость вращения).

Полученная модель достаточно сложна и неудобна для исследования из-за наличия переменной по времени t. Упростить решение данной системы можно заменой динамической моде- ли (1) на ряд статических моделей, т. е. разработать квазистатическую модель. Для этого произ- ведем замены времени t на текущий угол поворота инструмента ψ и величины отставания лезвий по времени τ на величину отставания лезвий по углу i·2π/z, где i – номер лезвия. В результате получим квазистатическую модель многолезвийного инструмента:

	( z .      (      i • 2 nY z x ■ (      i • 2 nY
•                      /       (      i • 2 n Y j • x ( v ) = X k ri "h i "cos I v         I• i = 1              V        z )	x ( v ) • cos I VI + У ( V ) • sin I VI S             V       z )            V        z ) +- z                     tg ϕ

( i • 2пY     ( i • 2пY ( i • 2пY . (    i • 2пYY x I v--I • cos| VI - УI VI • sin I VI

V z ) V z ) V z ) V z )

tgϕ z^

j • У ( V ) = - X k ri • h i • sin I V i = 1                ^V

-

i ⋅ 2 π z

⋅

(

S

7 +

x ( v ) • cos I V-

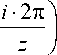
+ y ( v ) • sin I V-

tg ϕ

( i • 2 nY (      i • 2 nY (      i • 2 nY . ( i • 2 n Y)

x I v I • cos I VI - У I VI • sin I VI

V z ) V z ) V z ) V z )

tg ϕ

I                                                                             )

Перенеся в левую часть системы уравнений (2) члены, содержащие текущие координаты центра инструмента – x ( ψ ) и y ( ψ ), нетрудно представить в общем виде эту систему:

1 ^z

+ Y (V) •;--X Ki" hi" cos(V- tgϕ i=1

X ( v ) • J +-- X K i "h i " cos²( V- i • 2 n / z )

_    tg V tT

-i • 2n / z) • sin(v - i • 2n / z) = X K • hi • i=1

⋅ ( X ( ψ- i ⋅ 2 π / z ) ⋅ cos²( ψ- i ⋅ 2 π / z ) - tg ϕ

- Y ( ψ- i ⋅ 2 π / z ) ⋅ cos( ψ- i ⋅ 2 π / z ) ⋅ sin( ψ- i ⋅ 2 π / z )) - S / z ⋅ cos( ψ- i ⋅ 2 π / z ) ] ;

z

" • X K i x tg ϕ _{i = 1}

1                                                                                                        1

Y(v)---XKi" hi"sin(V-i• 2n/z)• cos(v-i• 2n/ z) + Y(v) • J + tgV i=1                                                      L xhi • sin2(v-i• 2n/z)! = XKi • hi  (X(V-i• 2n/z) • sin(v-i• 2n/z) • cos(v-J i=1        L tgv

-i • 2n/ z) - Y(v-i • 2n/ z) • sin2(v-i • 2n/ z)) -S/ z • sin(v-i • 2n/ z)J, где X(ψ) – текущая координата X центра инструмента в зависимости от угла его поворота; Y(ψ) – текущая координата Y оси инструмента в зависимости от угла его поворота; X(ψ-i⋅2/z) – запаздывающий аргумент X (значение аргумента X – i⋅2π/z угла поворота инструмента назад); Y(ψ -i⋅2/z) – запаздывающий аргумент Y (значение аргумента Y – i⋅ 2/z угла поворота инструмента назад).

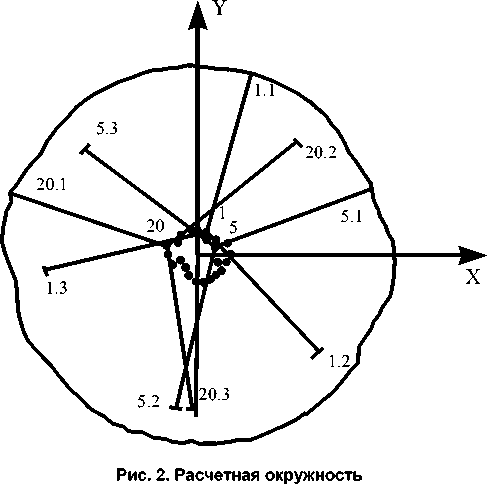
Рассмотрим решение системы (3) на ЭВМ. Для этого разобьем один полный оборот инструмента на несколько элементарных поворотов с углом Δ ψ , чтобы привести непрерывный процесс обработки, который при выбранной математической модели возможно решать только интегральным методом, к дискретному, поддающемуся итерации. В конце каждого такого элементарного поворота будем рассматривать одну расчетную точку. В итоге мы получим расчетную окружность (рис. 2), по которой, вычисляя в каждой расчетной точке X ( ψ ) и Y ( ψ ) отклонения центра инструмента, мы можем судить о поведении инструмента в течение данного оборота.

Технология

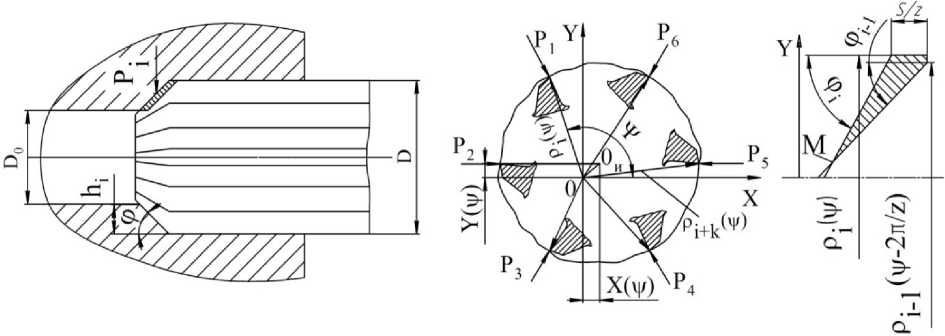
Рис. 1. Расчетная схема для модели многолезвийного инструмента

Теперь если сделать этот вычислительный процесс непрерывным до конца обработки, а именно для количества оборотов N = L/S, где L – длина обработки, то мы сможем судить о поведении инструмента на протяжении всего процесса обработки данным инструментом на данном технологическом переходе.

Рассмотрим структуру приведенной модели (3). В ней при искомых членах уравнений и в свободных членах стоят коэффициенты, содержащие знак суммирования по количеству лезвий инструмента. Поэтому, очевидно, что в алгоритме программы должен присутствовать цикл суммирования этих составляющих и он должен быть внутренним по отношению к циклу, организованному по расчетному кругу.

В свободных членах уравнения присутствуют так называемые запаздывающие аргументы X ( ψ- i ⋅ 2/ z ), Y ( ψ- i ⋅ 2/ z ), поэтому, для того чтобы иметь при моделировании процесса обработки эти запаздывающие аргументы, был разработан специальный алгоритмический прием, заключающийся в следующем. Общее количество расчетных кругов N разбивается на первый круг и N – 1 последующих кругов. В начале расчета значения запаздывающих аргументов принимают-

z

S

ся равными нулю, а активным является первый расчетный круг, именно с него запоминаются все аргументы X и Y .

В дальнейшем активными становятся N – 1 расчетные круги и значения аргументов X и Y последовательно переприсваива-ются первому расчетному кругу, с которого и берутся запаздывающие аргументы.

В итоге разработки, программирования, отладки и доказательства адекватности численной модели (3) выяснились некоторые неточности первоначально избранной математической модели, которая была выведена чисто аналитически без учета пропорций между теми или иными факторами, влияющими на процесс обработки. В результате приведенная и отлаженная математическая модель имеет следующий вид:

Y ( у ) • J • tg ф + £ K i • I h i + — • tg ф I• sin²( y   ( i- 1) • 2 n / z )

L           i = 1      ^ z ^

z

+ X ('H • £ Ki X i=1

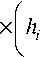
+ ⋅ tg ϕ z

sin2( ψ- ( i - 1) ⋅ 2 π / z ) 2

= Y ( у - 2 n / z ) • ]T K i • h i • sin² ( у - ( i - 1) X i = 1

^z         sin2( ψ- ( i - 1) ⋅ 2 π / z ) S^z

×2π/z)+X(ψ-2π/z)⋅∑Ki⋅hi⋅                         - ⋅tgϕ⋅∑Ki⋅hi× i=12                   z         i=1

× sin( ψ - ( i - 1) ⋅ 2 π / z ).                                                                                   (4)

Данная модель позволяет рассчитывать координаты Х и Y положения центра инструмента и по ним координаты профиля обработанной поверхности в продольном и поперечном сечениях. По этим координатам можно рассчитать погрешности обработки. В целом модель (4) описывает процесс формообразования отверстий с любым числом лезвий. Однако принятые в этой модели пропорции соотношений величин, необходимых при расчете площадей сечений срезаемых слоев (см. рис. 1), характерны для многолезвийных зенкеров и разверток.