L-устойчивость мульти-неявных методов 8-го порядка для жестких систем дифференциальных уравнений

Жесткие задачи встречаются во многих областях науки и техники, включая кинетику химических реакций, гидродинамику многофазных течений, приложения в биологии и другое. При численном решении таких задач возникает ряд проблем, связанных с устойчивостью, точностью и вычислительной сложностью применяемых методов. Наиболее полные обзоры по численным методам для жестких систем содержатся в [3; 6]. В настоящей работе рассматривается новое семейство разностных схем, которое является расширением семейства мульти-неявных схем со второй производной, представленных в [1; 7].

В приложениях численных методов для жестких систем центральной является проблема устойчивости методов. Требование абсолютной устойчивости неизбежно приводит к неявным разностным методам. Однако и для них существуют ограничения, например, порядковый барьер Далквиста [4; 5]: неявные линейные многошаговые методы выше второго порядка не могут быть А -устойчивыми. Однако для очень жестких задач условие A -устойчивости может оказаться недостаточным. Для них требуются L -устойчивые методы, простейшим примером которых является неявный метод Эйлера первого порядка.

Одним из видов численных методов, в которых возможно одновременно совместить высокие требования к устойчивости и порядку аппроксимации, являются неявные методы Рунге – Кутта [2]. Однако ресурсоемкость их реализации очень велика, что связано с необходимостью применения итерационного поиска решения на каждом шаге интегрирования. Для этого обычно применяется метод Ньютона, основные затраты которого заключаются в многократном вычислении матриц Якоби правой части системы уравнений. Если эти матрицы Якоби использовать в разностной схеме, то можно повысить порядок аппроксимации схемы без увеличения вычислительной сложности при ее реализации. Такой подход использован в многошаговых методах со второй производной.

В классических многошаговых методах используется информация в нескольких предшествующих точках. В противоположность этому в данной работе рассматриваются методы, которые используют несколько последующих точек, для каждой из которых записывается отдельное разностное уравнение. Такой подход приводит к построению семейства так называемых мульти-неявных методов со второй производной ( m-Implicit Second Derivative ). mISD -схема представляет собой систему разностных уравнений. Порядок аппроксимации отдельных уравнений можно варьировать с сохранением порядка схемы в целом, что позволяет расширить семейство mISD -схем. В данной работе подробно рассмотрено такое расширенное двухпараметрическое семейство для 3 ISD -схем. Показано, что среди множества A -устойчивых 3 ISD -схем существует два однопараметрических семейства: семейство L -устойчивых схем и семейство схем повышенной точности для линейных задач. Проведено тестирование таких разностных схем на линейной и нелинейной задачах с различной степенью жесткости. Представленные зависимости интегральной погрешности численного решения от величины шага интегрирования хорошо демонстрируют качество устойчивости и точности предлагаемых 3 ISD -схем.

1. Мульти-неявные методы со второй производной

Рассмотрим задачу Коши для автономной системы обыкновенных дифференциальных уравнений d-и(t) = f (и),        и(0) = и0,     t > 0,                             (1)

dt где и = {иi(t), и2(t), ... , up(t)}T и f(и) являются векторными функциями размерности p. Введем сетку {tn = т n, n = 0, 1, 2...} с постоянным шагом т > 0. Функции, определенные на сетке и приближенные решения обозначим как vn = v(tn), fn = f(vn).

Для численного решения задачи (1) предлагается m раз неявный разностный метод

m

-----' k = £ ( a ki E + T b ki J n ₊ i ) f n + i , k = 1,2,..., m ,                     (2)

^т              ,=0

где v i и f i - p -векторы. E и J - единичная матрица и матрица Якоби размера p х p :

f = f ( v i ),

т   дf, х ,

J; = -z-( Vj ),     ( i = n , n + 1,..., n + m ).

¹    д и

При известном v n = v ( t_n ) разностная схема (2) представляет собой систему взаимосвязанных нелинейных разностных уравнений относительно неизвестных v n +1 , v n +2 , ... v n + m в m последующих точках t n +1 , t n +2 , ... t n + m . Такую схему будем называть m- неявной.

Для нахождения коэффициентов разностной схемы (2) запишем ошибку аппроксимации, используя, что для решения системы (1) и выполнено и " = f_uu " = f_uf :

и — и

W k = —ⁿ------ n^ ₊ £ ^{( a} ki ^u n ₊ i + ^{т b} ki ^u n + i ),         k = ^1,2,...^, m .                  ⁽³⁾

^T            i = 0

Разложение функций, первых и вторых производных в (3) в ряд по степеням τ с центром в точке t n позволяет выписать систему линейных уравнений на коэффициенты, которые обеспечивают

W k ( t n ) = O( T ^{2 m + 2}),      k = 1,2,..., m .

Ниже приведены коэффициенты для случаев m = 2, 3 и 4 в матричной форме записи.

	101 F 240	128	11		13 F 240	— 1	— 1 80 I
При m = 2: ( aki ) =	11	240 128	240 101	,      ( b ki ) =	1	6 1	— 13
	H 240	240	240 K		H 80	6	240 K

При m = 3:

	6893	313	89	397	1283		— 851	— 269	— 163
	18144	672	672	18144		30240	3360	3360	30240
( a ki ) =	3	109	109	3	,      ( b ki ) =	31	113	— 113	— 31	.       (4)
	224	224	224	224		10080	1120	1120	10080
G	397	89	313	6893	G	163	269	851	— 1283
	H 18144	672	672	18144 K		H 30240	3360	3360	30240 K

При m = 4:

	1539551	89371	103	38341	59681		26051	- 31207	- 81	- 1243	- 2237 725760 I
	4354560	272160	630	272160	4354560		725760	90720	320	18144
G	26081	122341	313	12091	14111	G	893	6887	- 47	- 1721	- 103
( a ki ) =	4354560 14111	272160 12091	630 313	272160 122341	4354560 26081	,   ( b ki ) =	725760 103	90720 1721	320 47	90720 - 6887	145152 J - 893
	4354560	272160	630	272160	4354560		145152	90720	320	90720	725760
G	59681	38341	103	89371	1539551	G	2237	1243	81	31207	- 26051
	H 4354560	272160	630	272160	4354560 K		H 725760	18144	320	90720	725760 K

Разностные схемы с этими коэффициентами имеют соответственно 6-й, 8-й и 10-й порядок аппроксимации. Две первые были представлены в работах [1; 7]. Далее будем их именовать 2 ISD , 3 ISD и 4 ISD соответственно ( m-Implicit Second Derivative ).

Видно, что построенные разностные схемы обладают центральной симметрией для коэффициентов aki и антисимметрией для коэффициентов bki, а именно aki= am+1- k, m - i ,  bki=- bm+1-k, m- i, k = 1,... m i = 0,... m.(5)

Свойство (5) является следствием структуры разностной схемы. Несложно показать, что оно приводит к взаимной симметрии областей устойчивости и неустойчивости. Разностная схема называется абсолютно устойчивой, если численное решение модельного уравнения

-d^u(t) = Xu, X, и(t) e C, ReX < 0(6)

асимптотически стремится к нулю с ростом t при любой величине шага интегрирования τ . Применяя схему (2) к уравнению (6), получим однородную систему линейных уравнений (7) относительно v n , v n +1 , ... v n + m .

vn+k- vn+k-i=e(akiz+bkiz2) vn+i        k=i,2,-, m.

i = 0

Коэффициенты системы и, следовательно, само решение системы, зависят от z = Хт .

Устойчивость mISD -схемы разумно идентифицировать по крайним значениям решения системы (7). Функцией роста R m ( z ) для (7) назовем отношение

R m ( Z ) =        .                                            (8)

vn

Область S в комплексной плоскости, в которой модуль функции роста меньше единицы, называется областью устойчивости метода:

^{z e S} ° I R m ⁽ z )| <  1.                                  (9)

Несложно доказать, что в силу вещественности и симметрии коэффициентов (5) решение системы (7) обладает следующими свойствами.

Свойство 1. Если при z = ц решением является - = ( - _n , - _{n + 1},..., - _{n + m} ) , то при z = ^ решением будет w = ( - n , - n + 1 , ..., - n + m ) и, следовательно, R m ( ц ) = R m ( ц ) .

Свойство 2. Если при z = ц решением является - = ( -_n , -_{n + 1} ,..., -_{n + m} ), то при z = - ц решением будет w = ( - n + m , - n + m - 1 ,..., - n ) и, следовательно, R m ( - ц ) = [ R m ( ц )] ^{- 1}.

Из этих свойств, в частности, следует, что мнимая ось комплексной плоскости является границей области устойчивости, так как при симметрии относительно мнимой оси область устойчивости переходит в область неустойчивости. Если при этом у области устойчивости нет других границ, то она совпадает с левой комплексной полуплоскостью, и схема (3) будет являться A-устойчивой. Вопрос о других границах требует более детального рассмотрения функции роста.

При m = 2 функция роста найдена в [7]

104  ²     1   3    1   ⁴

R 2 (Z ) =

• ^{1    + z +} 240 ^{z +} 10 ^{z +} 90 ^z

104   2      1   3     1   4 .

• ^{1    z +} 240 ^z 10 ^{z +} 90 ^z

При m = 3 функция роста приведена в [1]

R з ( z ) =

3      29 2     3 3    193   4     11   5     1    6

^{1 +} 2 ^{z +} 28 ^{z +} 7 ^{z +} 1680 ^{z +} 560 ^{z +} 560 ^z

1 - 2 Z ⁺ 29 Z² 2     28

-

3 3    193   4

7 ^{z +} 1680 ^z

-

11   5      1    6

560 ^{z +} 560 ^z

.

В обоих приведенных случаях числитель и знаменатель отличаются только знаком при нечетных степенях, что приводит к равенству их модулей при чисто мнимых значениях z . Это подтверждает установленный факт, что мнимая ось является границей области устойчивости. Также видно, что для отрицательных действительных z во всех случаях | R ( z )| < 1. Известно, что такая дробно рациональная функция роста обеспечивает А -устойчивость, если все корни знаменателя лежат в правой полуплоскости.

Для всех mISD -схем это выполняется. В самом деле, комплексные корни знаменателя непрерывно зависят от коэффициентов многочлена, которые, в свою очередь, непрерывно зависят от коэффициентов разностной схемы (2). С помощью непрерывного изменения коэффициентов при сохранении их симметрии (5) любую разностную mISD -схему (2) можно трансформировать в более простую А -устойчивость схему, например, в совокупность однократно неявных схем 4-го порядка. При непрерывном изменении коэффициентов с сохранением их знаков и свойства симметрии (5) А -устойчивая схема (2) переходит в А -устойчивую. Следовательно, mISD -схема также будет A -устойчивой.

• 2 . Двухпараметрическое семейство 3 ISD -схем 8-го порядка

Рассмотрим семейство разностных 3 ISD -схем, в которых только для последнего значения обеспечивается максимальный 8-й порядок точности, а промежуточные значения вычисляются с порядком на 1 меньше. Для этого перепишем разностную схему (2) применительно к 3 ISD -схеме в ином виде, который может быть получен путем линейной комбинации отдельных разностных уравнений в (2):

n ^{+ 1} _Т n = L ( a « E + TbuJ n + i ) f- + i -

S n” *2, T vn =X (a '-.E + Tb2Jn +i) fn *1-(10)

2T= v” *3,-vn = ]3:( a 3,E + Tb3,J”+,) f”+,,

3Ti

Коэффициенты для метода, обеспечивающие 8-й порядок аппроксимации всех входящих уравнений в этом несимметричном виде, легко получаются из коэффициентов (4) путем линейной комбинации уравнений. Они имеют вид:

	6893 F 18144	313	89	397		1283 F 30240	- 851	- 269	- 163 Л 30240 I
		672	672	18144			3360	3360
G	223	10	13	10	G	43	- 8	- 19	- 4
( aki ) -	1134	21	42	567	,       ( bki ) -	1890	105	210	945 J
	31 H 224	81	81	31 224 K		19 H 1120	- 27	27	- 19 1120 K
		224	224				1120	1120

Порядок аппроксимации последнего разностного уравнения в (10) не изменится, если значения v _n + 1 и v _n + 2 в его правой части будут вычисляться лишь с 7-м порядком. Из этих соображений введем в первое и второе разностные уравнения по одному свободному параметру с одновременным уменьшением их порядка аппроксимации на 1, то есть до 7-го. В итоге получим двухпараметрическое семейство трижды неявных схем со следующими коэффициентами

	6893     11 18144 + 3 а	613 + 9 а	<872 - 9 а	397      11 18144   3 α I
( a ki ) -	223     11 1134 + 3 в	i + 9 в	i - 9 в	10      11 567   3 β		,
G	31	81	81	31
	224	224	224	224	K	.                    (11)
	1283 30240 + а	- 60 + 9 а	- 69 + 9 а	30240 + а
( b ki ) -	G 43 1890 + в	1 - 05 + 9 в	709 + 9 в	9445 + в	J
	G 19	- 27	27	- 19
	H 1120	1120	1120	1120 K

В частном случае а = в - 0 все три разностных уравнения в (10) имеют 8-й порядок аппроксимации.

Для аналитического вычисления функции роста схемы (11) требуется решить систему, коэффициентами которой являются квадратичные многочлены с неопределенными коэффициентами. Объем выкладок очень большой, однако, в силу того, что коэффициенты α и β разведены по разным уравнениям, определитель системы будет только линейно зависеть от упомянутых коэффициентов. Это значительно облегчает вывод аналитического выражения для функции роста, которая будет иметь следующий вид:

R ( z ) =

P ( z ) _ 1 + р 1 z + p ₂ z ² + p 3 z ³ + p 4 z ⁴ + p 5 z ⁵ + p 6 z⁶

Q ( z )    1 - q 1 z + q 2 z ² - q 3 z ³ + q 4 z ⁴ - q 5 z ⁵ + q 6 z ⁶

где

3                                       29   99      180                    3    69111

P 1 - T ^{- 9 а + 18 в} ,         p 2 ^- 28 - ~ ^{а +} ~ ^e ,      p 3 ^- 7 ^- "7" ^{а +} “ ^в,

193    27      36                     11    243      27                    127

p 4   1680   7 ^{а +} 7 ^в , p 5   560   280 ^{а +} 35 ^в ,     p 6   560   280 ^a ,

3                                       29   99      198                     3    111138

• ^q1   2 ' ^{9 а 1}8 ^е ,             q 2   28 ' 7 ^а    7 ^в ,         q 3   7 '   14 ^а 7 ^в ,

193    18      54                     11    27      243                      127

• ^q 4   1680 ⁺ 7 ^а 7 ^в , ^q 5   560 ⁺ 70 ^а   140 ^в ,        ^q 6   560   140 ^в ,

Для А -устойчивости требуется, чтобы

| P ( z )|

------< 1 для всех z : Re z <  0 . | Q ( z )|

Для этого достаточно, чтобы аналогичное неравенство выполнялось для мнимой оси, то есть

I Q ( iy )|² - I p ( iy )|² > 0,       V y ,                                    (13)

и чтобы все корни многочлена Q ( z ) лежали в правой полуплоскости. Так как в нашем случае условие для корней выполнено при а - в - 0, и корни непрерывно зависят от параметров, то (13)

будет описывать все множество А -устойчивых схем. Выражение для разности квадратов знаменателя имеет вид (выкладки опускаем)

2            2     2187                10   8                       27   2 1

I Q ( iy )|   I P ( iy )|     15680 ^{( a}   2 ^{в )}y [ 270 + ^{( a} + 2 ^{в )} + 15 y ( 27 ^{( a} + 2 ^{в ))].}

Отсюда видно, что (13) выполняется при α и β , удовлетворяющих неравенству:

a >  2 в

.

• ^- 145 . a + 2 ^е . 2.

В плоскости (α, β) область (14) изображена на рисунке 1 с границей ВСАЕ. Внутри области имеется семейство разностных схем, для которых обращается в нуль коэффициент p6 в числителе функции роста (a = 154 ). Это отрезок AB на рисунке 1. Он содержит семейство L1-устойчивых разностных схем. На отрезке AB имеется точка, в которой p5 = 0 (a = 154, в = - 1216 )• При этих параметрах получаем L2-устойчивую разностную схему. На рисунке 1 она отмечена буквой F.

Косвенную информацию о порядке аппроксимации разностной схемы можно получить из разности функции роста и соответствующей экспоненты. Для точного u и приближенного v решений модельного уравнения (6) выполняется un^3- = exp(3 z), un

v n + з = ^{P (} z ) v_n     Q ( z ) ^.

Их разность будет характеризовать погрешность метода для модельной задачи. Также, опуская выкладки, приведем аналитическое выражение для этой разности

exp(3 z) - P(z) = з246о(270

Q ( z )

- ( a + 2в))z 9 + 156800 ( 108 - (3 a + 4 в )) z ¹⁰

Q ( z )

.

Как и ожидалось, при нулевых параметрах метод имеет 8-й порядок точности, так как правая часть в (15) является O ( z ⁹). С помощью параметров можно повысить порядок точности. Семейство схем 9-го порядка задается условием a + 2 в = 1270 • Часть этой прямой попадает в область A -устойчивости и на рисунке 1 изображена штриховой линией. На ней примечательными являются две точки. Точка G ( a = 154 , в = - Ц₃₅ ), которая соответствует L i -устойчивой схеме 9-го порядка, и точка D ( a = Х40 , в = Ц₀₈₀ ), которая соответствует А -устойчивой схеме 10-го порядка. При этих значениях параметров обнуляется и коэффициент при z ¹⁰ в (15).

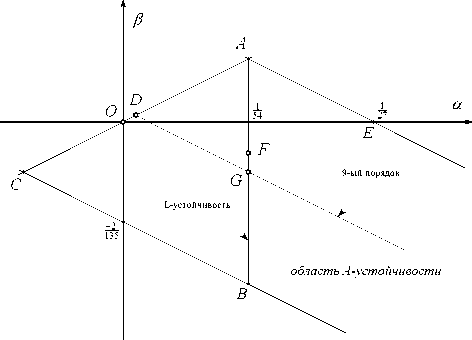
Рис. 1. Диаграмма состояний 3 ISD -схемы в плоскости свободных параметров ( α , β )

Заметим, что повышенная точность схем G и D , обнаруженная по функции роста модельного линейного уравнения, может не достигаться для нелинейных дифференциальных уравнений. Реализуемость этого свойства необходимо проверять на практических тестах.

Таким образом, для последующего тестирования отберем из семейства (10–11) четыре разностных схемы, которые соответствуют точкам O , D , G и F :

• 1)    A (8) - базовая А -устойчивая схема 8-го порядка ( а = 0, в = 0).

• 2)    A (10) - А -устойчивая схема 10-го порядка ( а = 1/ 540, в = 1/1080).

• 3)    L i (9) - L 1 -устойчивая схема 9-го порядка ( а = 1/54, в = — 1/135).

• 4)    L 2 (8) - L ₂-устойчивая схема 8-го порядка ( а = 1/54, в = — 1/216).

• 3.    Результаты тестирования 3ISD-схем

Тестирование проводилось на трех тестовых задачах, которые перечислены ниже.

Тест 1. Линейная система с постоянными коэффициентами. Первая стадия тестирования проводилась на примере численного решения линейной системы (16) с тремя переменными.

F — 2 — u ( t ) = - 8 dt G

H 1

-

1I

- 3   1 и ( t ) на t е [0,1] с начальными условиями и (0) =

2 - 12K

F1IGG1JJ

H1K

Матрица системы имеет как вещественные, так и комплексные собственные числа.

Тест 2. Жесткая нелинейная система без пограничного слоя. Дальнейшее тестирование проводилось на частном случае тестовой задачи Капса [2, с. 238], которая представляет собой жесткую (при p >> 1) автономную систему двух нелинейных дифференциальных уравнений и‘( t) = -(p + 2) и1 + pu 2

t е [0,2],

U 2 ( t ) — и — U 2 — U 2

с начальными условиями и 1 (0) = 1, и ₂(0) = 1. При этих условиях реализуется плавное решение является u 1 ( t ) = e ^- t , и₂(t ) = e ^- t ^/2 независящее от p (см. рис. 2, а ).

Тест 3. Жесткая нелинейная система с пограничным слоем. Та же система Капса, что и в предыдущем случае, но при иных начальных условиях и 1 (0) = 0, и ₂(0) = 1. В этом случае реализуется решение с переходной зоной (пограничный слой, см. рис. 2, б) , толщина которой 5 ~ 4/ p . График для решения (рис. 2, б ) имеет две типичные зоны поведения решения, характерные для жесткой компоненты. Первая зона включает быстрое изменение функции u 1 ( t ), когда она переходит к равновесному значению. Затем эта функция медленно меняется вблизи равновесного значения. Поведение второй компоненты мало зависит от параметра p . Она относится к так называемым медленным компонентам.

Во всех тестах выполнялось численное интегрирование с различными шагами τ по времени, и в конечной точке T оценивалась погрешность численного решения по разности между приближенным решением u и точным решением u *

\\u ( T ) - u * ( T )ll || u ^*( T )||

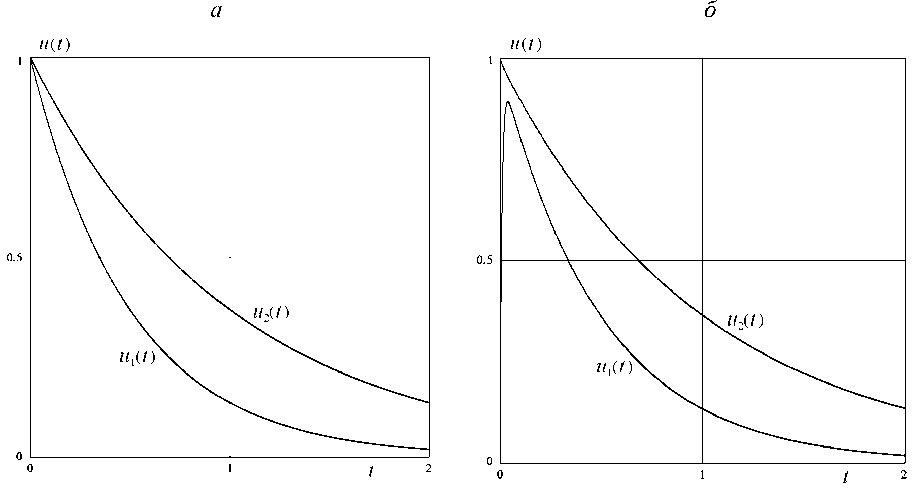
Рис. 2. Решение тестовой задачи (17) c параметром p = 100 при различных начальных условиях: а ) плавное решение; b ) решение с пограничным слоем

На рисунке 3 представлена зависимость ε ( τ ) в логарифмических осях для четырех вышеупомянутых схем. Контрольное решение предварительно рассчитывалось с максимально возможной точностью. Для лучшей идентификации кривых дополнительно черными кружками отмечены результаты для базовой схемы А (8).

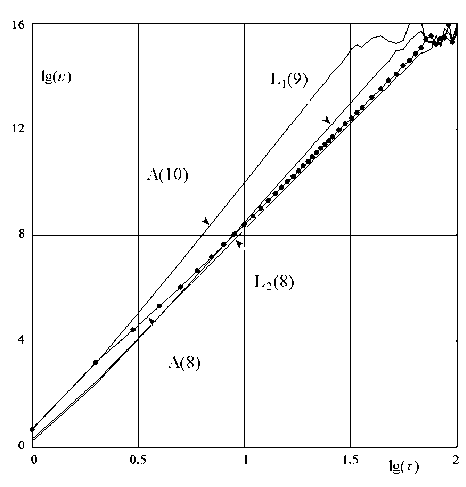
Рис. 3. Зависимость погрешности ε численного решения от величины шага интегрирования τ для различных вариантов 3ISD-схем на линейной задаче (16)

По углам наклона кривых в логарифмических осях хорошо видно, что порядки точности всех схем соответствуют теоретическим, за исключением начального и конечного участков. Хаотическое поведение погрешности в районе £ = 10 ^{- 15}-10 ^{- 16} объясняется пределом машинной точности. Данные расчеты проводились со стандартной двойной точностью формата вещественных чисел с мантиссой 52 бит.

а                                       б

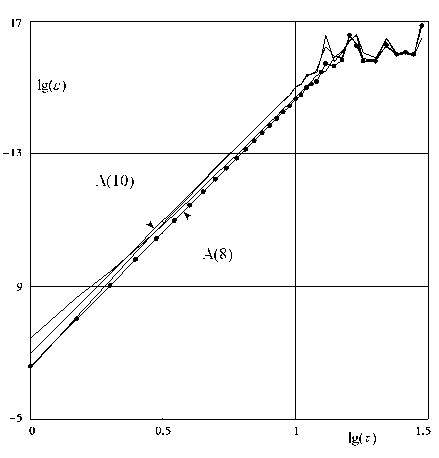
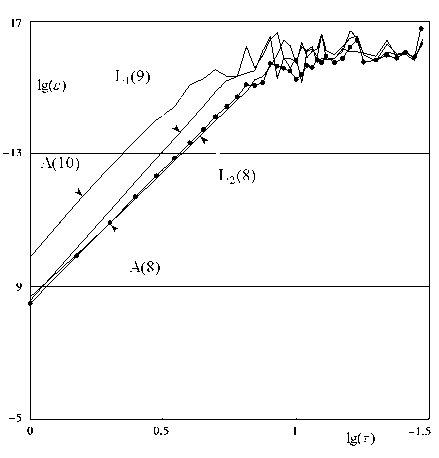
Рис. 4. Зависимость погрешности ε от величины шага интегрирования τ для различных вариантов

3 ISD -схем на плавном решении теста Капса (17): а ) p = 1; b ) p = 10 4

На рисунке 4 в логарифмических осях представлены зависимости погрешностей (18) от величины шага интегрирования для нежесткого ( p = 1) и жесткого ( р = 10 4 ) случаев на плавном решении (рис. 2, а ). На рисунке 4, а видно, что на нелинейной задаче преимущество в точности схем А (10) и L 1 (9) пропадает. Все тестируемые схемы имеют 8-й порядок точности, при небольшом преимуществе схемы А (10).

На рисунке 4, б представлены аналогичные результаты для жесткого случая. Видно, что качество расчета не ухудшилось, все схемы устойчивы, порядок точности не уменьшается. Опять проявляется преимущество схем А (10) и L 1 (9). Это связано с тем, что при больших значениях параметра p система приближается к линейной системе, и при этом начинают отчетливо проявляться преимущества схем повышенного порядка.

Следующее тестирование проведено для решения с пограничным слоем (рис. 2, б ). На рисунке 5 также в логарифмических осях представлены зависимости погрешностей от шага интегрирования для жесткого случая с p = 10³.

Видно, что поведение погрешности сильно меняется по сравнению с предыдущими тестами. Отчетливо видны недостатки строго А-устойчивых схем, которые плохо рассчитывают переходный процесс при большом числе жесткости. Для L-устойчивых схем таких проблем не возникает, в этом и заключается их главное преимущество. При данном числе жесткости преимущество L2 над L1 почти не видно, оно проявляется при большей жесткости. Почти во всем диапазоне графика на рисунке 5 шаг по времени т > 5, 5 - размер погра- ничного слоя. В результате погрешность крайне неравномерно распределена по отрезку интегрирования. Суммарная погрешность складывается из двух частей: ε 1 - погрешность на пограничном слое и ε 2 - погрешность на всем остальном участке интегрирования. Для методов А(8) и А(10) ε 1 очень большая. В этом и заключается главный их недостаток по сравнению с L-устойчивыми методами. Существенное отличие A-устойчивых методов от L-устойчивых исчезает лишь при τ ≤ 10δ.

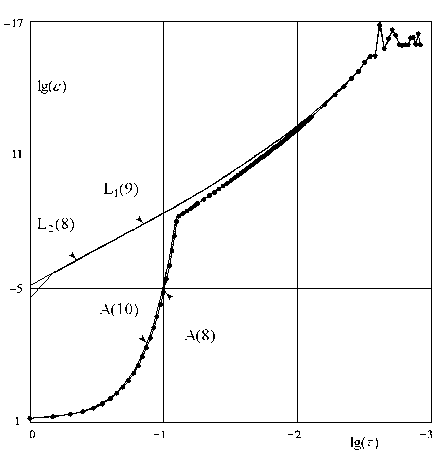
Рис. 5. Зависимость погрешности ε численного решения от величины шага τ для различных вариантов 3 ISD -схем на решении с пограничным слоем, тест № 3, p = 10³

Заключение

Суммируя изложенные результаты, отметим следующее. Предложенное расширенное семейство трижды неявных схем содержит несколько высокоэффективных представителей. По суммарной оценке устойчивости и точности по результатам тестирования выделяется L 1 -устойчивая схема 9-го порядка.