Лауэ-дифракция рентгеновских пучков в многослойной структуре

Многослойные структуры (МС) применяются в установках синхротронного излучения для транспортировки рентгеновских пучков, фокусирования излучения, при экстремальной ультрафиолетовой литографии (EUVL) и в астрономии. Преимущественно МС выполняют функции отражателей скользящего рентгеновского излучения. Для фокусировки жестких рентгеновских лучей предложено создать многослойные Лауэ линзы [1]. Теоретические основы рентгеновской дифракции такими линзами описаны в [2]. Изготовление многослойных Лауэ линз представляет собой сложную задачу, и первым шагом в этом направлении является изучение Лауэ-дифракции в МС с постоянным периодом [3]. Поэтому в данной работе рассмотрена теория Лауэ-дифракции рентгеновских микропучков в МС с использованием формализма для пространственно-ограниченных рентгеновских полей [4, 5].

1.    Динамическая Лауэ-дифракция ограниченных рентгеновских пучков в мультислое

Рассмотрим динамическую Лауэ-дифракцию рентгеновских лучей в секционированном мультислое с постоянным периодом d (рис. 1). Введем декартову систему координат: ось z направим вдоль облучаемой поверхности МС, а ось x — нормально к ней. На пути распространения исходной плоской волны на расстоянии LS1 от поверхности МС расположен пространственный ограничитель S1 (коллиматор, щель), который выделяет микропучок шириной w 1, падающий на поверхность МС под углом 6 = 6B + ш, где ш — малый угол отклонения. Амплитуду излучения на входной поверхности обозначим через E(in); амплитуду проходящей и дифракционной волн на выходной поверхности МС обозначим Eо и E 1 соответственно. Дифракционная интенсивность регистрируется позиционно-чувствительным детектором (PSD), расположенным на расстоянии LPSD от выходной поверхности МС.

Уравнения дифракции рентгеновских лучей в пространственно-периодических структурах [4, 5], с учетом граничных условий Лауэ-дифракции, дают решение для амплитуды дифракционного микропучка в обратном пространстве

E, , ( q - .q - ^expl L ’ F, , ( q - ,q , )

E 1 ( q . ) = i a ^{1 f} exp' i^L - ) F 1 ( Q x .q , ).

2 П

∞

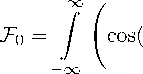
Lxξ т—-

^z sin( L^ ) £/ 2

K in ( к )d к

F - =7

-∞

^sin( LT ) ^/ 2

/X                  /X

K in ( к ) У _еж ( к

— qz )d к,

где ^ = — V Z ² + 4 fa 1 a - 1 , Z = q x — ( q z — 2 к ) tan 9 b , a 0 = пх о / ( X cos 9 b ) , a 1 = Cnx 1 / ( X cos 9 b ) , a - 1 = a i , 9 _b — угол Брэгга, X — длина волны рентгеновского излучения в вакууме, C — поляризационный фактор, f — фактор затухания, зависящий от дефектов в МС.

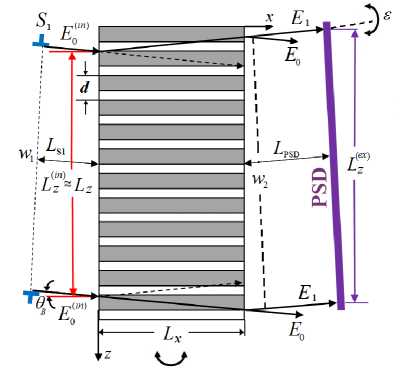
Рисунок 1. Схема Лауэ-дифракции в мультислое глубины L x и толщины L z : w i , ₂ — поперечная ширина падающего и выходящего пучков; L Zin ) , ⁽ ex ) — проекции на ось z (направлена вдоль входной грани) поперечной ширины пучка для падающего излучения и для вышедшего из мультислоя соответственно; L s 1 — расстояние от щели S 1 до входной грани мультислоя ( x = 0 ); L PSD — расстояние от выходной грани ( x = L x ) до позиционно-чувствительного детектора PSD.

Figure 1. Laue diffraction scheme in a multilayer structure with L x depth and L z thickness: w 1 , ₂ — cross-section width of incident and output beams; L Zin ) , ⁽ ex ) — cross-section projections of incident and the output beams onto the z axis (directed along the input face), respectively; L S ₁ — a distance from a S 1 slit to the multilayer’s input face ( x = 0 ); L PSD — a distance between the output face ( x = L x ) and the position-sensitive detector PSD.

Если период МС, как на рис. 1, образован бислоем вида d = d t + d b , то Фурье коэффициенты рентгеновской поляризуемости х о , 1 в направлении прохождения и дифракции равны

X t d t + X b d b

X о = -----3----- ,

d

χt - χb     πdt х 1 =         sin(

Здесь χ _t,b и d _t,b — Фурье коэффициенты поляризуемостей и толщины верхнего (t) и нижнего (b) слоев.

Распределение интенсивности рентгеновских волн в обратном пространстве при трехосевой схеме регистрации зависит от угловых положений образца ω и анализатора ε [6, 7]. В симметричной геометрии Лауэ эти углы связаны с проекциями отклонения вектора дифракции от вектора обратной решетки в горизонтальном и вертикальном направлениях соотношениями qx = k sin 9b (2ш — г) и qz = —k cos 9b г .Множитель Kin (к) в интеграле (1) выражает граничные условия дифракционной задачи на входной поверхности МС и имеет вид sin( к L (in))

K n ( к ) = P ( к,L s 1 ) -^к ,       (2)

где L zn ) = w 1 / cos 9 _b — ширина области на входной поверхности МС, засвечиваемая падающим микропучком; P ( к,L s 1 ) — пропагатор поля рентгеновской волны в Фурье пространстве [8], который в приближении Френеля равен                                       ₂

P ^{( к},^L s ₁) = exp (^—i^X L S ^{1 к}   ) .

4 п cos ² 9b /

Второй множитель

.                      sin ( ^zL ^e ) )

K ex ( к — q z ) = P ( к — q z , L psd )--- ^V _{K - q} z ------ (3)

2“ является коэффициентом пропускания дифракционной волны в Фурье пространстве. Он зависит от ширины отраженного рентгеновского пучка LZex) и выражается через пропагатор lpsd (к — qz)2

P ( к — q z ,L psd ) = exp —iX                ,

4п cos2 9b описывающий распространение рентгеновского излучения от выходной поверхности МС до PSD. Важно отметить, что в приближении геометрической оптики пропагаторы P(к,Ls 1) и P(к — qz,Lpsd) равны единице.

Окончательное выражение для дифракционной интенсивности в обратном пространстве, регистрируемой PSD при рассеянии ограниченного фронта рентгеновской волны в МС, запишется как

1 1 ( q x ,q z ) = IE 1 ( q x ,q z ) | ² •              (4)

Решения (1) с учетом (4) являются основными соотношениями для расчета карт рассеяния в обратном пространстве (RSM).

• 2.    Численное моделирование

  Выполним численное моделирование углового распределения интенсивности рассеяния рентгеновских лучей от МС M o/S i . Структурные параметры МС и характеристики падающего синхротронного излучения соответствуют параметрам и условиям работы [3]. Длина волны падающего синхротронного излучения X = 0 • 1305 нм, период МС d = d Mo + d _Si = 7 нм, d _Mo = d _Si = 3 • 5 нм, угол Брэгга 9 b = 2 • 25 мкрад. Оптические константы компонент МС получены с помощью онлайн сервиса рентгеновского сервера [9].

Динамическая Лауэ-дифракция рентгеновских лучей в МС сопровождается маятниковым эффектом (Pendellösung effect), когда интенсивность рентгеновского пучка проходящей волны перекачивается в дифракционный и далее, с увеличением глубины, наоборот, интенсивность дифрагированной волны передается в направление проходящего. При выполнении точного условия Брэгга выражения интенсивности для проходящей и дифракционной рентгеновских волн в МС равны

1 0 ( x ) = e ^ 0 x (cos ² ( fa 1 x) + sinh ² ( fa \ x )) ,

11 (x) = e ^0 x (sin2 (falx) + sinh2 (failx)) , ar = Cπχr1  ai = Cπχi1m

¹     λ cos θ B ^{, 1}     λ cos θ B ^,

где µ 0 = 2 Im( a 0 ) — линейный коэффициент поглощения, l Pen — период маятниковых осцилляций, который в симметричной геометрии Лауэ равен l Pen = λ | cos θ B | /C/|χ 1 | . При малых углах Брэгга cos θ B ≈ 1 , период маятниковых осцилляций обратно пропорционален Фурье коэффициенту рентгеновской поляризуемости χ 1 . Для рассматриваемого МС Mo/Si и длины волны рентгеновского пучка λ = 0 . 1305 нм период маятниковых колебаний равен l _P ^MoSi = 38 . 2 мкм.

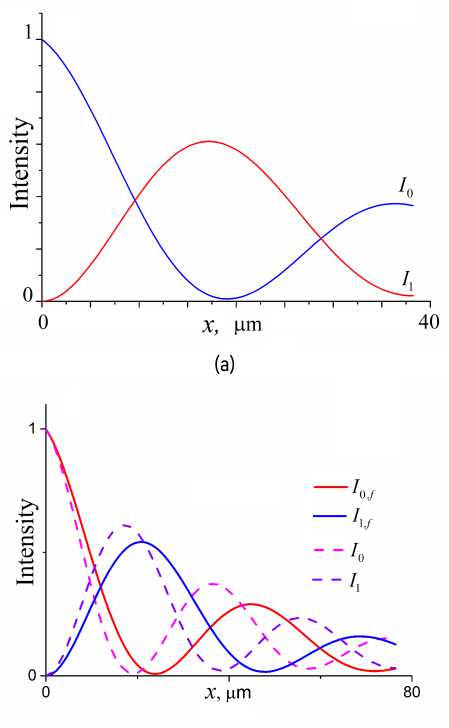
На рис. 2 представлены распределения интенсивности проходящей и дифракционной волн по глубине, иллюстрирующие маятниковый эффект при соблюдении точного условия Брэгга: пунктирными линиями показаны результаты в совершенном МС с фактором затухания f = 1 , а сплошными линиями — в дефектном с f = 0 . 8 . Толщина МС составляет L x = 2 l Pen = 76 . 4 мкм, что соответствует двум полным периодам маятниковых осцилляций. Рис. 2 (a) показывает, что при распространении рентгеновского пучка в МС интенсивность проходящей волны перекачивается в дифракционную. На глубине x = 19 . 1 мкм, отвечающей половине маятникового периода, проходящая волна переходит полностью (с поправкой на фотоэлектрическое поглощение) в дифракционную, которая достигает здесь локального максимума. С дальнейшим ростом x происходит обратный процесс. Рис. 2 (b) демонстрирует влияние дефектов. И него следует, что наличие дефектов в МС ведет к увеличению периода маятниковых осцилляций и смещению взаимного положения максимумов и минимумов интенсивностей I 0 ( x ) и I 1 ( x ) . Эти изменения объясняются тем, что дефекты в МС снижают отражательную способность периодической структуры. Аналогичное влияние дефектов на маятниковые осцилляции наблюдается в случае динамической Лауэ-дифракции в кристалле [10].

Зная глубину залегания максимумов и минимумов дифракционной интенсивности в МС Mo/Si , приступим к численному моделированию RSM. Расчеты выполним для МС с секционной толщиной L x = argmax( I 1 ( x )) = l _P ^MoSi / 2 = 19 . 2 мкм L x , при которой интенсивность дифракционной волны достигает максимума, и с толщиной L x = argmin( I 1 ( x )) = l _P ^MoSi = 38 . 2 мкм, отвечающей минимуму (рис. 2).

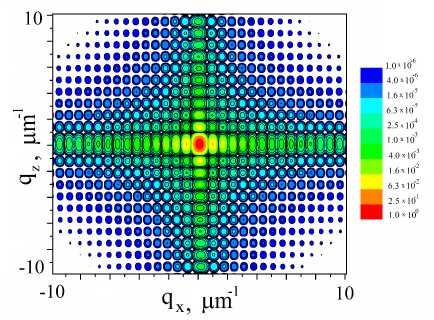
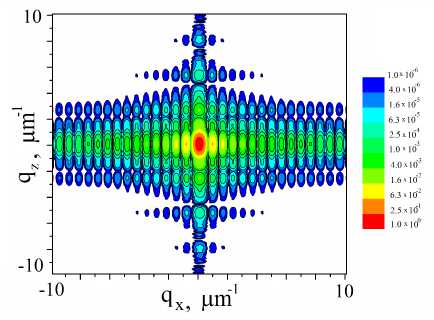
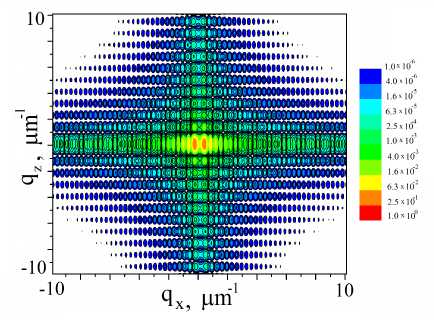
Результаты моделирования в рамках геометрической оптики для МС с L x = l _P ^MoSi / 2 приведены на рис. 3 (a), для МС с L x = l _P ^MoSi — на рис. 3 (b). Сравнивая между собой полученные карты, можно заметить, что для МС с секционной глубиной, равной полному периоду маятниковых осцилляций, возникает расщепление главного дифракци-

(b)

Рисунок 2. Маятниковый эффект (Pendelösung effect) в совершенном (a) и несовершенном (b) мультислое Mo/Si : кривые 1 0 j , 1 1 j — проходящая и дифракционная интенсивности в несовершенном мультислое c фактором затухания f = 0 . 8 ; кривые 1 0 , 1 1 — проходящая и дифракционная интенсивости в совершенном мультислое c фактором затухания f = 1 .

Figure 2. Pendelösung effect within perfect (a) and imperfect (b) Mo/Si multilayers: curves 1 0 j , 1 1 j — transmission and diffraction intensities in an imperfect multilayer with damping factor f = 0 . 8 ; curves I о , 1 1 — transmission and diffraction intensities in a perfect multilayer with damping factor f = 1 .

онного пика рис. 3 (b). Данное расщепление объясняется тем фактом, что в точных условиях Брэгга q x = q z = 0 на глубине x = L x = l _P ^MoSi основная часть дифракционной интенсивности перекачивается в проходящий пучок, из-за чего на RSM вблизи точки q x = q z = 0 возникает провал, но поскольку I 1 ( l _P ^MoSi ) не достигает нуля, то и значения интенсивности в окрестности данной точки не нулевые. Однако если угол падения будет отклоняться от точного условия Брэгга, то будет меняться характер распределения маятниковых осцилляций по глубине МС, в частности сократятся амплитуда и длина периода. В результате таких изменений интенсивность дифракционной волны в точке x = l _P ^MoSi не будет соответствовать положению минимума, что повлечет рост регистрируемой интенсивности. При определенных значениях угла ω может сложиться ситуация, при которой там, где при точном соблюдении условия Брэгга наблюдался минимум, расположится локальный максимум.

(a)

(a)

(b)

Рисунок 3. Карты рассеяния в обратном пространстве дифракционной интенсивности синхротронного излучения с энергией 9.5 кэВ от мультислоя M o/Si с граничными условиями в приближении геометрической оптики: (a) — L x = l MoSi / 2 ; (b) — L x = l MoSi .

Figure 3. Calculated RSMs of diffraction intensity from a Mo/Si multilayer with a synchrotron radiation energy of 9.5 keV in the case of the boundary conditions in the geometrical optics approximation: (a) — L x = l MoSi / 2 ; (b) — L x = l MoSi .

(b)

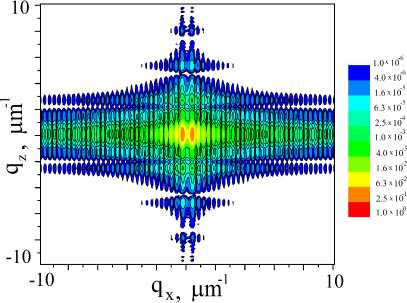
Рисунок 4. Карты рассеяния в обратном пространстве дифракционной интенсивности синхротронного излучения с энергией 9.5 кэВ от мультислоя Mo/Si с граничными условиями в приближении Френеля: (a) — L x = l MoSi / 2 ; (b) — L x = l MoSi ; L _s 1 =30 мм и L_P = 40 мм. Figure 4. Calculated RSMs of diffraction intensity from a Mo/Si multilayer with a synchrotron radiation energy of 9.5 keV in the case of Fresnel boundary conditions: (a) — L x = l MoSi / 2 ;(b) — L x = l Mo^Si ; L s 1 = 30 mm, L pdd = 40 mm.

Аналогичные расчеты выполним для пространственноограниченной рентгеновской волны с граничными условиями в приближении Френеля. Расстояние от щели до поверхности МС равно L S 1 = 30 мм, расстояние от выходной поверхности до PSD L P = 40 мм, ширина падающего пучка w 1 ^ L z = 14 мкм (см. рис. 1). Результаты моделирования представлены на рис. 4. Сравнивая полученные RSM с картами, представленными на рис. 3, легко заметить, что угловые распределения интенсивности рассеяния рентгеновских лучей в случае геометрической оптики и в приближении Френеля сильно отличаются. Тем не менее характерное расщепление центрального пика МС толщиной L x = l M ^oSi сохранилось.

Заключение

Таким образом, мы теоретически исследовали Лауэ-ди-фракцию рентгеновских микропучков в секционированных мультислоях. Как в геометрии Брэгга [4], так и для случая Лауэ-дифракции микропучков при выполнении расчетов RSM всегда необходимо правильно выбирать граничные условия в приближении Френеля. Важно, что решение (1) справедливо только для мультислоев с постоянным пери- одом. При исследовании апериодических многослойных структур необходимо численно интегрировать уравнения рентгеновской дифракции [2].