Лечебные физические упражнения при гипертензии

Суть включения исследовательских методов в образовательный процесс заключается в том, чтобы рассматривать исследовательские умения как важную задачу для каждой отдельной дисциплины или даже её раздела. Это и есть главная особенность такого подхода.

Исследовательские умения не формируются после одного-двух исследований. Педагогами разрабатываются индивидуальные карточки с заданиями для обучающихся, направленными на развитие конкретных умений, которые ещё не сформированы у ученика.

Чтобы карточка была эффективной и помогала ребёнку развиваться и формировать необходимые умения для проведения исследования, а не просто выполнять задания, она должна соответствовать определённым требованиям.

Токмазов Г.В. считает, что для решения геометрических задач (в том числе при итоговой аттестации в форме ЕГЭ) необходима система исследовательских умений [3,4].

Владимир Модестович Брадис сформулировал утверждение о том, что решение задач имеет цель развитие математического мышления и является первичной формой творческой исследовательской работы. В этом и заключается значение задач в школьном курсе математики. Необходимо обращать внимание учащихся на возможность различных вариантов решения одной и той же задачи, всячески поощрять поиск таких вариантов, заниматься сравнением и их оценкой, останавливаться на лучших».

По мнению Елены Олеговны Старковой, решение типовых задач школьного курса математики не приносит большого результата, а лишь ведёт к слабому овладению метапредметными умениями [2].

Ученик должен уметь:

• -    работать с задачами, которые отличаются от текстовых и для которых известен способ решения;

• -    искать новые или альтернативные способы решения задач и проводить исследования;

• -    работать с информацией в разных формах (текст, таблица, диаграмма, схема, рисунок, чертёж);

• -    отбирать информацию, если задача содержит избыточные данные; привлекать информацию и использовать личный опыт;

• -    моделировать ситуацию;

• -    задавать необходимую точность данных с учётом условий задачи;

• -    применять здравый смысл, метод перебора возможных вариантов и проб и ошибок;

• -    представлять обоснование решения в словесной форме;

• -    учитывать все условия, необходимые для решения задачи и его интерпретации, и удерживать их в памяти.

Как уже было отмечено при описании уровней сформированности исследовательских умений, все учащиеся уникальны и имеют свой собственный уровень владения познавательными универсальными действиями логического и алгоритмического характера. При создании заданий важно учитывать индивидуальные особенности учеников.

При разработке и использовании математических заданий в обучении необходимо соблюдать ряд дидактических и методических требований.

Анализ литературы позволяет выделить три группы требований к созданию заданий [1, с. 46]:

Описательная часть заданий первой группы:

• 1.    Математические умения. Задания, сформулированные вне предметной области, должны отражать практическую информацию и решаться с использованием предметных математических знаний.

• 2.    Когнитивная сфера. Задания должны быть составлены с учётом уровня развития когнитивной сферы и умений решать задачи разными способами.

• 3.    Готовность к взаимодействию. При составлении заданий необходимо учитывать сформированность готовности взаимодействовать с математической стороной окружающего мира — умение погружаться в реальные ситуации (отдельные задания; цепочки заданий, объединённых ситуацией; проектные работы).

• 4.    Компетенции. Задания нужно разрабатывать с учётом сформированности коммуникативных, читательских, информационных и социальных компетенций.

• 5.    Регулятивная сфера. В заданиях следует учитывать умения: планировать деятельность, конструировать алгоритмы (вычисления, построения и пр.), контролировать процесс и результат, выполнять проверку на соответствие исходным данным и правдоподобие, корректировать и оценивать результаты деятельности.

Вторая группа требований связана с математическим содержанием прикладной задачи и с дидактическими принципами обучения:

• 1.    Системность. Задание должно соответствовать базовым знаниям учащихся. Например, задача на нахождение площади параллелограмма

• 2.    Избыток или недостаток данных. Задание может содержать данные, которые не нужны для решения, или, наоборот, содержать недостаток данных, которые требуется восстановить самостоятельно, используя имеющийся материал или жизненный опыт.

• 3.    Целостное применение математики. Задание должно быть не только понятно обучающемуся, но и предполагать формулировку проблемы на языке математики, её решение, а также представление и оценку полученного результата.

• 4.    Использование наглядности. В задании могут присутствовать таблицы, графики, диаграммы и т. д.

подойдёт для учеников, которые уже изучили эту тему. Если же учащиеся пока остановились только на признаках и свойствах этой фигуры, то такое задание не будет соответствовать их базовым знаниям.

Пример задания: в прямоугольнике длины сторон равны 6,7 см и 4,2 см, а площадь равна 28,14 см². Требуется найти периметр прямоугольника.

Ученики могут прийти к выводу, что площадь — это лишнее данное, поскольку для нахождения периметра прямоугольника нужны только длины двух его сторон.

Третья группа требований связана с комплексным подходом к постановке заданий:

• 1.    Основа. Все задания комплекса должны иметь единую основу.

• 2.    Последовательность. Каждое следующее задание комплекса должно дополнять предыдущее, обеспечивая логический переход от одного задания к другому.

• 3.    Сложность заданий. Материалы должны располагаться в порядке возрастания сложности. Не стоит начинать с самого трудного задания, так как это не даст ученику возможности постепенно выполнять их и нарушит логическую последовательность. Разделение задач на уровни сложности представлено в таблице.

Таблица 1

Уровни сложности заданий

Уровни	Характеристика
Низкий	предполагает одношаговую процедуру (выполнение одного действия): -    распознание термина или понятия -    преобразование выражения -    выполнение вычисления и т.д.
Средний	предполагает: -    установление связей -    интеграцию материала -    объяснение и использование различных данных в виде схем, графиков и т.п.
Высокий	предполагает: - анализ сложной информации

- обобщение информации - ее обоснование - формулирование выводов

На основе анализа литературы, содержащей информацию о требованиях к разработке заданий по математике, можно выделить единую структуру для каждого задания, представленную на схеме.

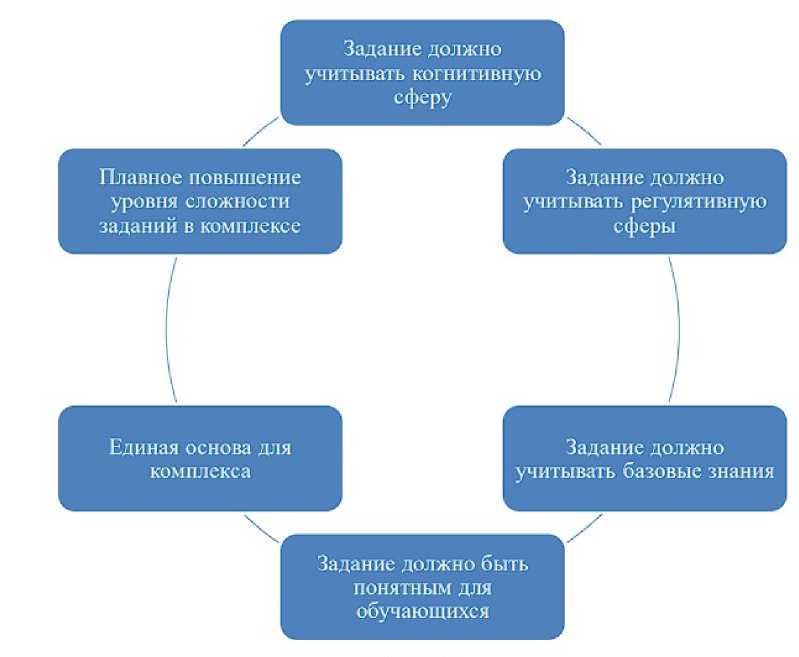
Схема 1 «Основные требования для разработки задания»

Главная задача при разработке заданий - создать индивидуальную образовательную программу и обеспечить разноуровневое обучение.

Если правильно подобрать материалы для заданий и учесть степень сложности, можно улучшить сформированность определённых навыков у каждого ученика или группы учеников.