Linear Crossed Cube (LCQ): A New Interconnection Network Topology for Massively Parallel System

Interconnection network has been usually recognized to be the most practical model of parallel computing. The numerous interconnection network topologies have been proposed and studied in the literature [1] [2] [3]. The binary n-cube also known as hypercube [HC] is a well- known network because it possesses quite a few desirable features. It includes highly fault- tolerance, low degree and small diameter. Nevertheless, the crucial disadvantage of hypercube and also its variation are difficulty of its VLSI layout, Scalability and Modularity [4] [5] [6]. It is usually needed that the size of the network i.e. the number of processing elements (nodes) can be increased with minimum or virtually no alternation in the existing configuration. Furthermore, the increase in the size should never degrade the overall performance of the final system. A large number of hypercube variant have also been reported, most notable are crossed cube (CQ) [7], Exchange Hypercube (EH) [8], Extended Crossed cube (ECQ) [9], Star graph S(n) [10], Star Cube (SC) [11] and Star Crossed Cube (SCQ) [12] etc. A CQ is derived from an HC by changing the way of connection in HC links. The diameter of a CQ is almost half of that of its corresponding HC. Specifically, from an n-dimensional HC having n-diameter, an n-dimensional CQ could be formed, which has a diameter equal to (n+1)/2. However, the CQ make no improvement in the hardware cost as the number of links drastically increase when extended to higher level of architecture [13]. EH is an excellent topology with the lower hardware cost [8]. An EH is based on link removal from an HC, which makes the network more cost-effective as it scales up. Unfortunately, the availability of rich connectivity in the EH is reduced [8]. The EH offers major reduction in the hardware cost compared to the HC, but no improvement over the diameter of the HC. The demand for reduction of the diameter of the HC as well as its hardware cost motivates our investigation in proposing a new interconnection network. The Extended crossed cube (ECQ) interconnection topology retains most of the topological features of the EH, and at the same time combines many attractive features of the CQ. In particular, the ECQ has the smaller diameter but also reduces the hardware cost. Moreover, the diameter of an

ECQ is almost the same as that of a CQ, but much smaller than that of an EH.

The Star graph S (n) has been widely used as an alternative to hypercube [10] [14]. The important feature of star graph are fault tolerance, partition ability and easy routing and broadcasting. The major drawback of S (n) is increasing complexity with higher value to the next higher dimension. For the improvement of star graph, another variation of star graph is introduced called Star Cube (n, m). When compared with star S(n), the growth of S(n, m) is comparatively small and smallest possible structure contains twenty four nodes with node degree equal to four [11]. A S (n, m) is edges-symmetric, maximally fault tolerant and cost effective. The Star crossed cube S (m, n) is derived from product of Star graph and Crossed cube. It is very suitable for variable node size architectures. The Diameter of a SCQ (m, n) is almost half of that of its corresponding Star cube. Specifically, the diameter of SCQ (m, n) is [ p (m+1)/2n + L (3(n-1))/2J] and the diameter of SC (n, m) is [m + ^ (3(n-1))/2^]. However, the SCQ (m, n) makes no improvement in the node degree compared to the SC (n, m).

While preserving most of the desirable properties of hypercube the important issues are the accommodation of more number of processing elements with lesser interconnection hardware and less communication delay. Exponential expansion has always been a major drawback of hypercube networks. Increasing number of nodes in the network also reduces the system reliability and assumed to be fault intolerant [14] [15]. Recently a Linearly Extensible Cube (LEC) network has been reported which employs lesser number of nodes with smaller diameter [16] [17]. The author claims various desirable topological properties while keeping the number of nodes lesser. Other attempts for designing such hybrid topologies are Hyper-star, Hyper-mesh, arrangement star network and Double-loop Hypercube etc. [18] [19] [20] [21]. The objective of this paper is to utilize this concept of hybrid architecture to make the network less complex while preserving desirable network properties.

Beside good topological properties it is also important that how much efficiently a parallel algorithm is mapped on a particular multiprocessor network. For instance the CQ is an important version of hypercube with smaller diameter but having a complex routing [12]. The overall performance of multiprocessor network depends how the processors exchange message reliability and efficiently. Over the year, many different interconnection networks along with appropriate scheduling scheme have been used in commercially available concurrent systems [22] [23] [24] [25] [26]. The aim of scheduling policy is to optimize some performance among multiple nodes and provide load balancing coupled with high scalability and availability [27] [28] [29]. The different techniques to optimize the network performance are scheduling the tasks or simply the task assignment, load balancing and load sharing. In task scheduling each parallel process is viewed as a collection of related tasks and these tasks are scheduled to suitable nodes evenly [30] [31] [32]. The aim is to assure that no node should remain idle and the distribution of tasks is made in such a way that the load on individual node should remain balance at any point of time. In the present work a simple dynamic scheduling scheme known as Minimum Distance Scheduling (MDS) which operate on the principle of minimum distance property has been implemented on the proposed LCQ interconnection network. The load is distributed dynamically and the proposed system considers load balancing as an online problem and scheduling is made on the fly.

The rest of the paper is organized as follows: section 2 presents the architectural details of proposed LCQ along with its topological properties. In section 3, the properties of other similar multiprocessor architectures are described and a comparative study is carried out. The performance of the proposed network is evaluated by implementing standard dynamic scheduling scheme on it as well as on other multiprocessor architectures. The simulation results are discussed in section 4. Finally, section 5 concludes the paper.

• II.    Linear Crossed Cube

Definition: The Proposed LCQ network is undirected graph and grows linearly in cube like shape.

Let q be the set of designated processor of Q thus, q ={Pi}, 0 < i < N-1

The Link functions E1 and E2 define the mapping from q to Q as.

E1(Pi) = P(i+2) ModN; ∀ Pi in q       (1)

E2 (Pi) = P(i+3) ModN           (2)

The two function E1 and E2 indicate the links between various processors in the network.

Let Z be a set of N identical processors, represented as

Z= {P0, P1, P2....... PN-1}

The Total number of processor in the network is given by

N =                        (3)

Where n is the depth of the network. For different depth, network having 1, 3, 6, 10, 15, 21,...... processors are possible. The arrangement is shown in Figure 1.

РЮ	РИ
Р22	Р31
Р43	Р53

Table 1. Properties Of LCQ Multiprocessor Network

Level	0	1	2	3	4	5	6	7	8	9	10	11	15
Number of processors	0	1	3	6	10	15	21	28	36	45	55	66	120
Diameter	0	0	1	2	2	3	4	5	6	8	9	11	20
Degree	0	2	3	4	4	4	4	4	4	4	4	4	4

Fig. 1. Arrangement of Processor in LCQ.

In order to define the link functions, we denote each processor in a set K as P in , n being the level/depth in LCQ where, the processor P i resides. As per the LCQ extension policy, one and two processors exist at level/ depth n. Thus at level 1, P₀ and P₁ exit and similarly at level 2, P₂ and P₃ exist as shows in Figure 2.

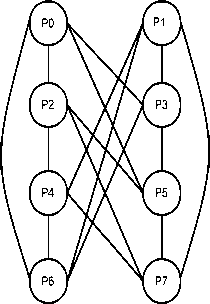
Fig. 2. Linear Crossed Cube With Eight Processors.

• A. Topological Properties of LCQ

The following are the various topological properties of the LCQ network.

Theorem 1. The total number of nodes in the LCQ is

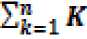
Proof: The total number of nodes in CQ (n) is 2n nodes. The LCQ is an undirected graph, where the total number of nodes is given below:

N =£ft = l^ e.g. {1, 3, 6, 15, 21......}

It shows that the network grows linearly, where 1≤ K ≤ n, n is the level number up to which the network is designed.

Theorem 2. The degree of nodes of LCQ is 4.

Proof: In CQ (n), the degree of nodes is defined as the total number of edges (n-1) incident on each vertex. Hence, the degree of each vertex in the LCQ is remain constant i.e. 4 irrespective of the depth of network. The behavior is shown in Table 1.

Theorem 3. The diameter of the LCQ is (└√N┘).

Proof: The diameter of network is the maximum eccentricity of any node in the network. It is the greatest distance between any pair of nodes. In LCQ, it is observed that the diameter does not always increase with the addition of a layer of processors. It may be highlighted that the diameter of LCQ shows a maximum value of 20 for 120 processors. This behavior is also demonstrated in Table 1. The diameter (D) may be obtained as:

D= (└√N┘)                (4)

Theorem 4. The Cost of LCQ.

Proof : The node degree of a LCQ is always constant which is equal to 4, however, the diameter is √N. The cost could be obtained as the product of the degree and diameter. Therefore, the cost is dependent on the value of diameter.

Cost = degree * diameter

Cost = 4*(└√N┘)                (5)

Theorem 6. The Extensibility of LCQ is (n+1).

Proof: The major advantage of proposed LCQ network is that its extension could be carried out in a linear fashion by adding one or two nodes in every extension. When single or odd number of nodes is added, we call it odd extension and similarly an even extension can be made by adding two or more even number of nodes in particular extension. The important feature is that the proposed LCQ does not have an exponential extension. Figure 3 shows the extensibility of LCQ network in different ways.

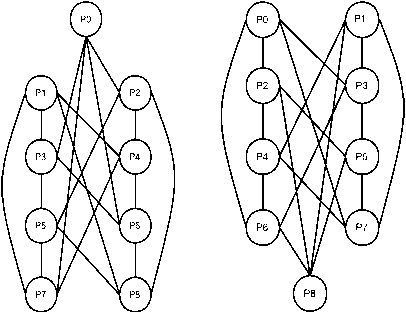
3(a) Upward odd extension 3(b) Downward odd extension

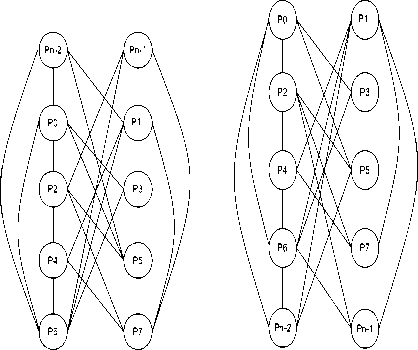
3(c) Upward even extension

3(d) Downward even extension

Fig. 3. Extensibility of LCQ.

Table 2. Summary of Various Parameters of different Multiprocessor Network

Paramete r	HC	CQ	SC	SCQ	LEC	LCQ
Number of Nodes	2n	2n	n!2m	n!2m	2n	Zk
Diameter	n	n	m+L3(n-1)/2J	(m+1)/2q + L3(n-1)/2J	LnJ	( l^nJ )
Degree	n	rn+1/2q	m+n-1	m+n-1	4	4
Cost	n2	nг|:"h 2n	(m+n-1)*(m+L3(n-1)/2J )	(m+n-1)( r(m+1)/21 + L3(n-1)/2J )	4LnJ	4( L.NJ)

Among the better known architectures on which much work has been carried out in particular are HC, CQ and SCQ. The LEC is another architecture which is different from HC however, possess some useful properties. Motivated by the properties of LEC, CQ and SCQ the proposed LCQ network has been designed. The above topological properties are analyzed with the above mentioned architectures. The values of various parameters are evaluated mathematically for comparison purpose. Table 2 gives a summary of various parameters for different type of multiprocessor networks.

• III.    Comprative Study

To make a final conclusion a comparative study of various properties is carried out. We consider three important parameters namely, number of processor, diameter and node degree. The large number of nodes and a high value of degree make the network complex, low diameter is always better because it determine the distance involved in communication and hence the performance of multiprocessor systems. The curves are plotted for each of the parameters for LCQ, LEC, SCQ, HC and CQ. The HC, CQ and SCQ have same pattern of increasing number of processors at various level of architectures and exponential expansion is obtained in all the cases as depicted in Figure 4. The important point here to mention is that all these networks attain larger numerical values even at lesser number of levels. In LEC, however, the number of processors are lesser as compared to HC, CQ and SCQ networks at greater levels. On the other hand LCQ shows better results from the other networks and the number of processor increases linearly with an addition of even or odd processors at each level of extension. This feature is not available in LEC network. However, it reflects important aspects of a multiprocessor system particularly when a less complex network is desired.

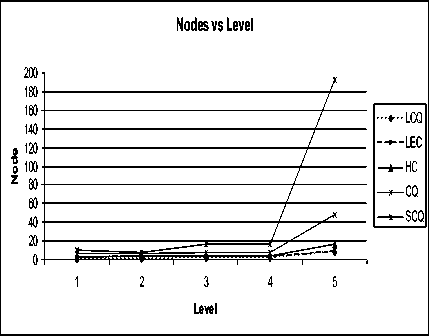
Fig. 4. Number of Processors of Various Multiprocessor Architectures.

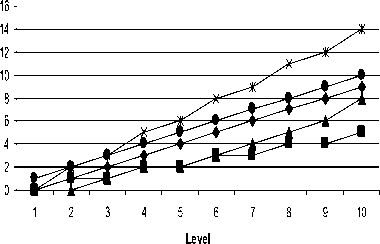
The second important parameter of LCQ and other multiprocessor architectures when analyzing the properties of these architectures is diameter. Figure 5 illustrates the different values of diameter obtained for various multiprocessor architectures. The study of results in the curve clearly shows that the LCQ architectures has lesser diameter as compared to other multiprocessor networks (Figure 5).

Diameter vs Level

A LCQ

-1- LEC

-+- HC

-е- CQ

SCQ

Fig. 5. Diameter of Various Multiprocessor Architectures.

Node degree is another cost effective parameter which has a greater impact on the complexity of network. The degree of a multiprocessor network defines the largest degree of all the vertices on its graph representation. When analyzing the networks in terms of node degree, the comparative study shows that all the network are having comparable values of the node degree while considering equal number of nodes. In particular, the LEC and CQ are having lesser values of the node degree compare with HC and SCQ. Though, the CQ is having lesser node degree but the system complexity increases with the increase in the number of processors. The LCQ is having variation in node degree at third level, however, after third level, it is constant and always equal to 4 as depicted in Table 1.

Degree vs Level

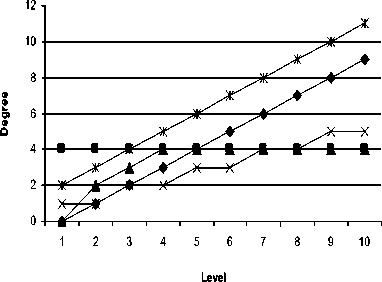
Fig. 6. Degree of Various Multiprocessor Architectures.

The LCQ network is motivated by the LEC network, however, the LEC may be considered as a special case of LCQ network as far as the number of processors and node degree are taken into consideration. Figure 6 shows that the degree in both the networks is same but the diameter and cost of LCQ are appreciably reduced as compared to LEC network.

Cost vs Level о о

LEC

LCQ

Level

1     2     3     4     5     6     7     8     9     10

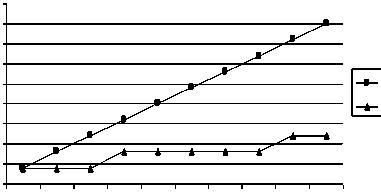
Fig. 7. Comparison of cost of LEC and LCQ network.

For symmetric network the cost factor is a widely used parameter in performance evaluation which is dependent upon node degree and diameter. Since LCQ has a smaller diameter in comparison to LEC network, therefore, LCQ exhibits better cost effectiveness as compared to LEC network. This trend is shown in Figure 7.

• IV.    Performance Analysis

In large scale parallel system, managing communication between various processing elements (nodes) is big problem, which considers how the processors exchange messages efficiently and reliably. To map the task on network of nodes the important concepts widely used called the scheduling algorithm. Several scheduling schemes have been reported that manage the distribution of load on a multiprocessor network dynamically and efficiently [18] [20] [21]. In the proposed work we have tested the performance of cube based networks by applying a simple scheduling algorithm known as Minimum Distance scheduling scheme (MDS) [18]. This algorithm is based on the principle of minimum distance feature. The basic approach in MDS is to optimize the load balancing among nodes under the constraint of the need to keep message lengths to one hop and thus satisfying the minimum distance property. Migration from donor node is made to the directly connected nodes. Thus, for every donor, there is a set of Minimum Distance Acceptors (MDA). For load balancing, the above mentioned (MDS) scheme calculates the value of Ideal Load (IL) at each stage of the load. IL is the load a processor is having when the network is fully balanced. The processors having a load value greater than the IL are considered as overloaded processors. Similarly, processors having lesser load than the value of IL are termed as under loaded processors. Each donor processor, during balancing, selects tasks for migration to the various connected and under loaded processors. The IL is used as a threshold to detect load imbalances and make load migration decisions. Migration of task can take place between donor and acceptor processors only.

The Load imbalance factor for i th level, denoted as LIF i , is defined as:

LIF i = [{load i (P k )} - (ideal_load) i ] / (ideal_load) i (6) where,

(ideal_load) i = [load k (P 0 ) + load k (P 1 ) + .......+ load i

(P N-1 )] / N                                                   (7)

and max (loadi (Pi)) denotes the maximum load pertaining to level i on a processor Pi , 0 ≤ i ≤ N-1, and loadi (Pk) stands for the load on processor Pi due to ith level.

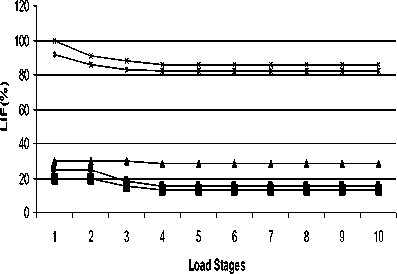
The algorithm is applied on LCQ, LEC, HC, CQ and SCQ networks. For the purpose of simulation we assume a simple problem characterization in which the load is partitioned in to a number of tasks. All tasks are independent and may be executed on any processor in any sequence. The performance has been evaluated by simulating artificial dynamic load on the different networks. It is characterized as a group of task structure i.e. uniform load. The results are obtained by implementing the MDS scheme on various multiprocessor networks under the same environment. The simulation run consist of generating uniform load imbalance is obtained for various stages of the tasks structures and the curves are plotted as the average percent imbalance against the load for different stages and shown in Figure 8.

LIF vs Load

+ LCQ

LEC

-*- HC

CQ

SQ

Fig. 8. Simulation of Load on Various Multiprocessor Architectures.

It is clear from the curves that all the networks are showing similar pattern when distributing and balancing the tasks. However, the performance of HC, LEC and LCQ is showing better results as the number of tasks increases. When we compare the initial values of imbalance it is observed that HC and LEC are having larger value (30%) as compared to LCQ. The LCQ is producing better performance as having an initial value of 20% which is continuously decreasing. CQ and SCQ having larger values of load imbalance and they remain larger even for higher level of task structure. This behavior is shown in Table 3.

Table 3. Performance of Various Multiprocessor Networks with MDS Scheme

Network	Max. of LIF (%)	Min of LIF (%)	Avg. Balancing Time up to 10 level (msec)
LCQ	41	29	101
HC	54	49	138
CC	42	38	160
LEC	42	31	133
SCQ	42	38	160

The results shown in Table 3 indicates that the standard algorithm (MDS) though giving the Minimum and Maximum imbalance percentage same in all the types of multiprocessor networks, however, in general it makes the network fully balance at higher level of task structure as compared to other scheduling schemes. The reason might be that the algorithm manages task assignment when greater volume of task is available on the network. The Standard algorithm is particular showing good results when applied on LCQ architecture in terms of initial value of load imbalance as well as distributing the tasks over various nodes of the system.

Another parameter to evaluate the performance of the proposed LCQ network when MDS scheme is implemented on it is the time taken to make the network fully balanced. The generation of tasks is assumed to be uniform at each level of the task structure. The respective average LIF’s along with the time taken to set the minimum value of LIF is evaluated at each level of task structure for various multiprocessor architectures.

To analyzed the behavior of average time the curves are plotted as the total average time against the number of level (Task Structure) and shown in Figure 9. It is clear from the curves that LCQ always utilizes lesser time to make the network fully balanced as compared to other similar multiprocessor networks. The combine effect of LIF and the balancing time demonstrated that the propose LCQ network out performing when conventional scheduling techniques is applied on to it.

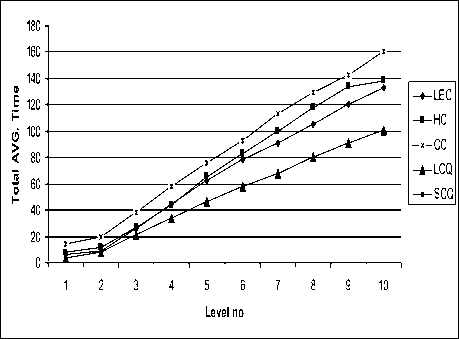
Fig. 9. Total Average Time of Various Multiprocessor Architectures

• V.    Conclusions

In this paper a new network topology named as Linear Crossed Cube has been proposed and considered as a variant of hypercube architecture. The proposed topology is a hybrid topology and effort is made to combine the desirable features of hypercube architecture and compact LEC architecture. The proposed architecture exhibits better connectivity, lesser number of nodes, lesser diameter and linear extension. The linear extension can be made with a layer of single or double processors. The node degree of the proposed LCQ is always constant which makes the network economical.

The performance of LCQ has been tested by implementing standard dynamic scheduling scheme on to it as well as on other similar multiprocessor architectures. The performance parameters namely load imbalance factor and balancing time are obtained and analyzed. The comparative simulation study shows that the above mention parameters are performing well on the proposed LCQ network. Therefore, it can be concluded that the proposed LCQ network is a low cost, easily extensible and scalable multiprocessor architecture and also capable to utilize all the available nodes efficiently when appropriate scheduling scheme is implemented on it. For future works, we intend to design more efficient scheduling scheme suitable for the purposed LCQ network.