Linear operators on abramovich--wickstead type spaces

CD 0 -type spaces were firstly introduced by Yu. A. Abramovich and A. W. Wickstead in [1] and [2] and further investigated by S. Alpay and Z. Ercan in [3]. CD 0 -type spaces deserve to be called Abramovich–Wickstead spaces, or briefly AW -space as in [4], since they mainly stem from the works of Yu. A. Abramovich and A. W. Wickstead. In this note we construct a new type AW -space and call it CD ₀ ^r for the sake of convenience.

Throughout this note, the symbols L ^r and L ^r _n denote the space of regular and order continuous regular operators respectively. For unexplained terminology about vector lattice theory, we refer to [5].

The first section is devoted to some introductory knowledge about vector-valued measures. This section will be useful in obtaining main results. For more detailed information about vector-valued measures, we refer to [6]. The second section of this note contains the definition of C D ₀ ^r -spaces. The third section is devoted to description of regular operators charactreziations about linear operators on C D ₀ ^r -space by means of vector measures and order summation. The fourth section contains two main results of the paper. In this section we are mainly interested in regular and order continuous regular operators on CD ₀ ^r -space with values in Dedekind complete vector lattices.

1.    Vector Measures

Consider a nonempty set K and a σ -algebra A of the subsets of K . Let E be a Dedekind complete vector lattice. We shall call the mapping ^ : A ^ E a vector measure if ^( 0 ) = 0 and for every sequence (A n ) of pairwise disjoint sets A n E A the equality holds

µ

∞

U An n=1

∞

= E^ ( A n )

n =1

n

= o - lim V ^ ( A k ).

n k=1

We say that a measure ^ is positive and write ^ >  0 if ^(A) >  0 for all A E A . We denote the set of all order bounded E -valued measures on a ст -algebra A by cab(K, A , E). If ^, v E cab(K, A , E) and t E R, then we put by definition

(° 2008 Polat F.

• (1)    (ц + V)(A) := ц(A) + V(A) (A e A ) ,

• (2)    (tц)(A) := tц(A) (A e A ) ,

• (3)    ц >  v о ц — v >  0 .

One can prove that cab(K, A, E) is a Dedekind complete vector lattice. In particular, every measure ц : A ^ E has the positive part ц+ := ц V 0 and the negative part ц- := (— ц)+ = —ц Л 0. It is easy to verify that ц+ (A) = sup{ц(A0) : A e A, A0 c A} (A e A).

In the sequel, we shall consider special E -valued measures. Suppose that K is a compact topological space and A is the Borel ст -algebra. A positive measure ц : A ^ E is said to be regular if for every A ∈ A we have

ц(A) = inf{ц(и) : A c U,U e Op(K)} where Op(K) is the collection of all open subsets of K. If the latter condition is true only for closed A e A, then ц is called quasiregular. Finally, an arbitrary measure ц : A ^ E is said to be regular (quasiregular) if the positive measures ц+ and ц- are regular (quasiregular). Let rca(K, E) and qca(K, E) be the sets of regular and quasiregular E-valued Borel measures respectively. It is seen from the definitions that rca(K, E) and qca(K, E) are vector sublattices in cab(K, A, E). Clearly, the supremum (infimum) of the increasing (decreasing) family of quasiregular measures bounded in cab(A, A, E) will also be quasiregular. The same holds for regular measures. Thus qca(K, E) and rca(K, E) are Dedekind complete vector lattices.

We now define the integral with respect to an arbitrary measure ц e cab(K, A , E ) . Let us denote by St(K, A ) the set of step functions ^ : K ^ R of the form ^ = ^2n ₌₁ a k X A k , where A i ,..., A n e A , a i ,... ,a n e R, and X A is the characteristic function of a set A . Construct the operator I ^ : St(K, A ) ^ E by putting

n

Iµ     ak XAk k=i

n

:= ^ak ц ( A k ).

k =i

As it is seen I µ is a linear operator. Moreover the following normative inequality holds

IW)| 6 kf UM(K) (f e St(K, A)), where kf ||^ = supkGK |f (k)|. The subspace St(K, A) is dense with respect to the norm in the space l^(K, A) of all bounded A-measurable functions on K. Therefore I^ admits a unique linear extension by continuity to l^(K, A), with the above-mentioned normative inequality being preserved. In particular, if K is a compact space and A is the Borel σ-algebra, then I^(f) is defined for every continuous function f e C(K). Note also that I^ > 0 if and only if ц > 0.

Finally, we give the following result of J. D. M. Wright [7] about analytical representation of linear operators which will play an important role to obtain main results of this note.

Theorem 1. Let K be a compact topological space and let E be an arbitrary Dedekind complete vector lattice. The mapping µ 7→ I µ implements a linear and lattice isomorphism of Dedekind complete vector lattices qca ( K,E ) and L ^r ( C ( K ) ,E ).

• 2.    CD 0 (K, E) -spaces

In this section we introduce a new class of Abramovich–Wickstead type spaces. We start with the following definition which contains the building blocks of this space.

Definition 2. For a compact space K and a relatively uniformly complete vector lattice E , we set

• (1)    C ( K,E ( e' )') the space of all mappings from K into E (e) which are continuous in the sense of the norm || • ||_e where E(e) denotes the ideal generated by e G E + and

||u H e := inf { A > 0 : | u | 6 Ae } ( u G E (e)).

Then, we set

Cr(K, E) := [ ©C(K, E(e)) : e G E+} and call the elements of this set r-continuous or uniformly continuous functions on K.

It is clear that C _r ( K,E) is contained in l ^ ( K,E ) , the space of order bounded functions from K into E , since in E (e) norm boundedness coincides with order boundedness. Moreover, C _r ( K, E) is a vector sublattice in l ^ ( K, E ) .

• (2)    C o (K, E(e)) the space of all mappings d from K into E (e) such that for all e >  0 the set { k G K : | d(k) | _e >  e } is finite. Then we set

c o (K, E ) := [ © c o (K, E (e)) : e G E ⁺ } .

It is clear that c o (K, E) is contained in l ^ ( K, E) . Moreover, c o (K, E) is a vector sublattice in l ^ (K, E ) .

Now we give the following theorem which will be useful in the sequel.

Theorem 3. Let K be a compact space. For any f G C _r ( K,E) and e >  0 there exist e G E ⁺ and finite collections a 1 , • • • ,a n G C ( K ) and e i ,..., e _n G E such that

n

6 εe.

sup α ∈ K

f (a) — ^2^k (a)ek k=1

C If f G C _r ( K,E ) , then f G C ( K,E (e)) for some e G E ⁺ . According to the Kakutani-Krein Theorem, E (e) is linearly isometric and lattice isomorphic to C (Q) for some compact Hausdorff space Q . Therefore one can assume that f G C ( K,C (Q)) . However, the spaces C ( K,C (Q)) and C ( K x Q) are isomorphic as Banach lattices. It remains to note that, according to the Stone–Weierstrass Theorem, the subspace of the functions n

(a, q) ^   O L a ) (a)e k (q) , where a ₁ ,---,a n G C ( K ) and e ₁ ,...,e _n G C (Q) , is dense in

C ( K x Q)^

Definition 4. Let K be a compact Hausdorff space without isolated points and E be a relatively uniformly complete vector lattice. We denote by CD o ( K,E ) the set of E -valued functions on K each of which is the sum of two E -valued functions f and d with f G C _r ( K, E ) and d G c o ( K, E ) .

For a finite subset S of K and e G E , X S ® e is in CD o KC,E\ It is easy to see that CD q ( K, E) is an ordered vector space under the pointwise order.

Lemma 5. Let K be a compact Hausdorff space without isolated points and E be a relatively uniformly complete vector lattice. Then, C _r ( K, E ) П C o (K, E ) = { 0 } .

C Suppose the contrary; let 0 = f E C r ( K, E ) П c g (K, E ) . Assume that f (x) = 0 . So there exists e E E + such that f E C ( K, E(e)) . Then there exists a neighborhood V of x such that for y E V we have k f (y) k e >  k f (x) | _e /2 . But since x is not isolated, V is uncountable, which is a contradiction since f E c g ( K, E) . B

It now follows that the decomposition of an element of CD g ( K, E ) -space into a sum of an r -continuous function and one with countable support is unique. So CD g ( K,E) deserves to be an Abramovich–Wickstead type space.

Lemma 6. Let K be a compact Hausdorff space without isolated points and E be a relatively uniformly complete vector lattice. Let p E CD g ( K, E ). Then p + = sup(p, 0) exists in CD g ( K, E ).

C Let p E CD g ( K,E ) . Let r ( k ) = f ⁺ (k) + [ - f ^— (k) + h(k)] V ( - f ⁺ (k)) for each k E K where f and h are continuous and discrete parts of p , respectively. By definitions f and h take their values in E (e) for some e E E ⁺ . Let s(k) = ( - f ^— (k) + h(k)) V ( - f ⁺ (k)) . Let e >  0 be given. Then there exists n g E N such that

{ k E K : e 6 ||s(k) k e } C kk E K : — 6 k h(k) k e) . I no J

Indeed, if this were not true, then for some sequence (kn) in K, we would have e 6 |s(kn)ke while |h(kn)ke < 1 for all n E N. By compactness of K, we can find a subnet (ka) of kn that converges to some kg E K. As |h(ka)|e — 0 in E(e), we have that e 6 |s(ka)ke = k(-f-(ka) + h(ka)) V (-f + (ka))ke - k - f-(kg) V (-f +(kg))|e = 0

which is a contradiction. Hence r E CD g ( K, E ) whenever p E CD g ( K, E) . On the other hand,

r(k) = f + (k) + [-f- (k) + h(k)] V (-f+ (k)) = [f+ (k) - f- (k) + h(k)] V 0 = (p(k)) + for each k E K .So r is indeed p+. Continuous part of r is f+, where f +(k) = (f (k))+ by uniqueness of decomposition. B

We summarize what we have from the previous proposition as follows:

Proposition 7. Let K be a compact Hausdorff space without isolated points and E be a relatively uniforly complete vector lattice. Then CD g ( K,E ) is a vector lattice under the pointwise ordering: 0 6 p E CD g ( K, E ) О 0 6 p(k) in E for all k E K .

Just like real-valued function space CD g ( K ) in [2], suprema and infima are easy to identify in CD g ( K, E ) . We shall write h Y t h if the net h Y is increasing and sup(h Y ) = h.

Proposition 8. Let K be a compact Hausdorff space without isolated points and E be a relatively uniformly complete vector lattice. If h Y t h in CD g ( K,E ), then h Y (k) t h(k) in E for all k ∈ K .

C Let k g be an arbitrary but fixed point of K . Then h ( k g ) is an upper bound of { h Y ( k g ) : Y E Г } in E (e) for some e E E ⁺ . Let v be another upper bound for { h Y (k g ) : y E Г } . If v Л h(k g ) = h(k g ) , then the proof is obvious. On the other hand, if v Л h(k g ) < h(k g ) , then we can find some 0 < e i E E(e) such that v Л h ( k g ) + e i 6 h(k g ) . Then h - X k ₀ 0 e i is an upper bound in CD g ( K, E ) for the family { h Y : Y E Г } , contradicting the definition of h . B

From the proposition above, we conclude that order convergence in CD g ( K,E ) is pointwise, order convergence in E .

• 3.    Linear operators on C r ( K,E) and c g (K, E)

Throughout this section, unless stated otherwise, E will denote a relatively uniformly complete vector lattice and for a vector valued function f , χ k ⊗ f will denote the function which takes f (k) at k and 0 otherwise. In this section we give two characterizations about the regular and order continuous linear operators from CD' ir ( K, E ) into a Dedekind complete vector lattice F .

We start with the following lemma which will be used in the sequel.

Lemma 9. Let K be a compact space and F be a Dedekind complete vector lattice. Then for every regular operator T : C r ( K,E) ^ F there exists a regular operator T 0 : C ( K ) ^ L^r ( E,F ) such that

T ( y 0 e) = T 0 ( y ) e for all y E C ( K ) and e E E.

The correspondence T → T ⁰ is linear positive, and one-to-one.

C It is sufficient to consider positive linear operators. Let T : C r ( K, E ) ^ F be a positive linear operator. For each y E C ( K ) and e E E, the function y 0 e defined by y 0 e ^{( k )} = y^{( k )}e belongs to C r ( K, E ) . We put

T ( y 0 e ) = T 0 ( y ) e for all y E C ( K ) and e E E.

For fixed y E C ( K ) , the mapping T 0 ( y ) : e ^ T 0 ( y ) e of E into F is evidently linear. Moreover, if 0 6 e E E and 0 6 y E C ( K ) , then T 0 ( y ) e = T ( y 0 e) >  0 , therefore T 0 (y) E L ₊ ( E,F ) . Thus, the mapping T 0 : y ^ T 0 ( y ) of C ( K ) into L r (E, F ) is linear and positive.

It is easy to verify that the mapping T → T ⁰ is linear and positive. In order to prove that this mapping is one-to-one, let S : C r ( K, E ) ^ F be a positive linear operator such that

S ( y 0 e) = T 0 ( y ) e, for y E C ( K ) and e E E.

Let f E C r ( K, E ) . Then by Theorem 3, there exists a sequence ( f n ) of the form ^2 y i 0 e i (finite sum) with y i E C ( K ) and e i E E converging relatively uniformly to f . Then T ( f n ) = S ( f n ) for every n . On the other hand T and S are relatively uniformly continuous on C r ( K,E ) , therefore

T(f) = lim T(fn = lim S(fn) = S(f), n→∞ n→∞ consequently T = S. B

Theorem 10. Let K be a compact topological space and F be a Dedekind complete vector lattice. Then there exists a lattice isomorphism T ⁰ ↔ µ between the set of regular operators T ⁰ : C ( K ) ^ L r ( E,F ) and the set of countably additive quasiregular Borel measures у : K ^ L r ( E, F ) given by the equality

T 0 ( f ) = j fdy,

for every f E C ( K ).

C Proof directly follows from Theorem 1, since L r ( E,F ) is a Dedekind complete vector lattice. B

Let F be another Dedekind complete vector lattice and у E qca(K, L r ( E,F )) . Then the integral I ^ : C ( K ) ^ E can be extended to C r ( K,E~ ) . We can view the algebraic tensor

Linear operators on a new AW (Abramovich–Wickstead)-space 51 product C(K) 0 E as the subspace in Cr(K, E), consisting of the mappings k ^ 52П=1 Vi(k)ei (k E K) where ei E E and Vi E C(K). Define I^ on C(K) 0 E by the formula nn

У V i 0 e i := У ei / V i d^ i =i         /     i=i k

If f E C r ( K,E ) , then by Theorem 3 there exist e E E + and a sequence ( f n ) C C ( K ) 0 E sup | f (k) - f n (k) | 6 ¹ e.

k ∈ K                ⁿ

Put by definition j fdц := I^(f) := o-lim I^(fn).

K

It can be easily seen that this definition is correct even for an arbitrary order bounded finitely additive vector measure µ .

Theorem 11. For any linear operator T E L r ( C r ( K, E ), F ) there exists a unique vector measure ц := ц т E qca(K, L r ( E,F )) such that

Tf = jf (k) dц(k) (f E C r (K, E)).

K

The correspondence T ^ ц _т is a lattice isomorphism of L r ( C r ( K,E ) ,F ) onto qca(K, L r (E, F)).

C See [6, Theorem 2.1.14 (5)]. B

Theorem 12. There exists a lattice isomorphism T ↔ T ⁰ between the space of regular operators T : C r ( K, E) ^ F and the space of regular operators T 0 : C ( K ) ^ L r (E, F ) given by the equality

T ( v 0 e) = T 0 ( v ) e,   for V E C ( K ) and e E E.

If T and T ⁰ are in correspondence, then there exists a unique common countably additive quasiregular Borel measure ц := ц т : K ^ L r (E, F ) such that

T (f ) = j fdЦ,

for f E C r (K, E ),

and

T 0 ⁽V⁾ = /

ϕ dµ,

for v E C ( K ).

In particulal, the correspondence T ^ ц _т is a lattice isomorphism of L^T( C r ( K,E),F ) onto qca(K, L r (E,F)).

C Let first T : C r ( K,E ) ^ F be a regular operator. Let T 0 : C ( K ) ^ L r (E, F) be the regular operator corresponding to T (Lemma 9) by the equality

T ( v 0 x) = T 0 (v)x, for V E C ( K ) and x E E.

We know that the correspondence T → T ⁰ is linear, positive, and one-to-one. We have

T ( v 0 x) = T 0 ( v ) x =

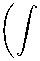
x for every x ∈ E , therefore

T (у 0 x) = j v 0 xd^,

for every у G C ( K ) and x 6 E.

Conversely, let T 0 : C ( K ) ^ L r ( E,F ) be a regular operator, and let ^ : K ^ L r ( E,F ) be the countably additive quasiregular measure corresponding to T ⁰ by Theorem 10. If we put

T(f)= jf^,  f G Cr(K, E), then T : Cr (K, E) ^ F is a regular operator and we have

T ( v 0 x) = T 0 ( v ) x, for V G C ( K ) and x G E.

It remains to apply Theorem 11. B

Now we give the following definition which will be useful in the sequel.

Definition 13. Let K be a non-empty set and F be a Dedekind complete vector lattice. Then we define

• (1)    c 0 ( N , E) = { ( e n ) C E : 3 e G E + such that e n G E (e) V n and k e n k e ^ 0 } ,

• (2)    l i [K,L ^r ( E,F )] is the space of maps a : K ^ L r ( E,F ) such that PP | a(k n ) | ( | e n | ) n =1

exists in F for all sequences ( k n ) G K and ( e n ) G c o ( N , E) .

∞ m

As usual, ^2 | a(k _n ) | ( | e _n | ) is the supremum of the sums ^2 | a(k _n ) | ( | e _n | ) . Clearly, n =1                                                n =1

l ₁ [K, L r (E, F)] is a vector lattice under the pointwise operations and ordering.

Theorem 14. Let K and F be as above. Then L r (c o (K, E), F ) is lattice isomorphic to l 1 [K,L ^r (E, F)].

• <1    Let ф : L r (c o (K, E),F) ^ l ₁ [K, L(E, F)] be defined by ф(G)(k)(e) = G ( x k 0 e) for each G G L r (c o (K, E ) , F ) , k G K and e G E . Then ф(G)(k) is a regular operator from E into F as ф(G ⁺ )(k) and ф(G ^- )(k) are positive for each regular operator G . Thus ф(G) is a map from K into L r (E, F ) and ф(G)(k)(e) >  0 whenever e >  0 and G >  0 , i. e. ф(G)(k) is positive for all G >  0 .

∞

Let us recall that ф(G) should also satisfy ^2 ^(G)(kn)l(|enD G F for all sequences (kn) G K and (en) G c0(N,E). Let G G Lr(c0(K,EyF). Then we have mm

£ BG)(k„)|(B|) = £ |G|(Xkn0|en|) = |G| n=1                   n=1

m

X n=1

χ k _n ⊗ | e n |

6 | G |

∞

X n=1

χ k _n ⊗ | e n |

∈ F,

therefore

∞ m

£ |ф(G)(k n ) | ( | e n | ) = sup£ | G | (x k n 0 | e n | ) G F.

m n =1                       n =1

Thus the map ф(G) we have defined belongs to l ₁ [K, L ( E, F )] .

It is easy to verify that φ is a linear mapping. We now show that it is bipositive. Suppose that ф(G) > 0 for some G G Lr(co(K, E),F), and take 0 6 f G co(K, E). As P Xk 0 f Ts f k∈S in co(K, E), we have P G(xk 0 f) ^ G(f). By definition G(xk 0 f) = ф(G)(k)(f (k)) > 0 k∈S and thus G(f) > 0 for each 0 6 f G co(K, E), i. e. G > 0.

Let now ф(G) = 0 for some G E L r (c o (K, E ) ,F ) . Then G ( x k 0 f) = 0 for each k E K and and 0 6 f E c o ( K,E ) . As P X k 0 f T s f in c o ( k, E) , we have 0 = P G ( x k 0 f ) ^ G ( f ) or k ∈ S                                         k ∈ S

G ( f ) = 0 . The fact that c o (K, E) is vector lattice leads to G = 0 .

To show that ф is surjective, let 0 6 a E 1 i [ K,L ^r ( E,F )] . Let f E c o ( K,E ) . Then there exists an at most countable subset ( k n ) of K such that f (k) = 0 for all k = k n and there exists some e E E + such that f ( k n ) E E (e) for each n and k f (k n ) k e ^ 0 . Hence we can define

G(f ) = X a(kn)(f (kn)), n∈N which certainly belongs to F as f (kn) E c0(N, E). We now verify that ф(G) = a. Let 0 6 e E E, then

ф(G)(k o )(e) = G(x k o 0 e) = X a(k o )(x k o 0 e) = a(k o )(e).

n ∈ N

Since e E E is arbitrary, we conclude that ф(G)(k o ) = a(k o ) and k o is arbitrary, we have ф(G) = a . Since l i [ K,L ^r ( E,F )] is a vector lattice, the proof of surjectivity of ф is now complete. B

4.    Main resalts

Now we are in a position to give one of the first main result of this note as follows:

Theorem 15. Let K be a compact Hausdorff space without isolated points and F be a Dedekind complete vector lattice. Then Lr(CD0(K,E),F) is lattice isomorphic to qca(K, Lr (E, F) © 11 [K, Lr (E, F)] with the dual order on this direct sum defined by hц,а) > 0 О ц > 0 and a > 0 and ц({k}) > a(k)

for all k ∈ K , which if we identify α with a discrete measure on K , is precisely requiring that ц >  a >  0.

• <1 Let T E L^T ( CD 0 ( K,E],F ) . Then certainly T splits into two regular operators T 1 and T 2 , where T : C _r ( K, E ) ^ F and T 2 : c o (K, E ) ^ F . By Theorem 12 there exists a measure ц E qca(K, L^T ( E, F ) such that T can be identified with ц . On the other hand, by Theorem 14 there exists a map a E l i [K, L r (E, F )] such that T 2 can be identified with a . We thus have a map from L r (CD 0 (K, E ), F ) into qca(K, L r (E, F) © 1 1 [K, L ^r (E, F)] .

  Now suppose that ц E qca(K, L r (E, F )) and a E 1 i [K, L r (E, F )] . We can certainly define

  
  

  an operator ϕ by

  
  

V(f) = [ fi Йц + X a(kn)(f2(kn)), n∈N for f = f1 + f2 E Cr (K, E) © Co(K, E). The map we have defined from qca(K, Lr (E, F)) © 11 [K, Lr(E, F)] into Lr(CD0(K, E), F) is easily seen to be lattice isomorphism by Theorem 12 and Theorem 14. B

Now we give the following definition which will be used in our final result.

Definition 16. Let K be a compact space and F be a Dedekind complete vector lattice.

Then we set 1 1 (K, L n (E, F )) the set of all maps в from K into L n (E, F ) satisfying

• (1)    sup P | e(k) | ( | (f (k) | ) exist in F for all e E E + and f E C ( K,E (e)) © c o (K, E(e)) , k f k e 6 1 k ∈ K

• (2)    P i e ( k ) l ( f a ( k )) ^ a 0 whenever f a I 0.

k ∈ K

As usual, 22 1в(k)|(|(f (k)|) is the supremum of the sums 22 |e(k)|(|f (k)|) where S is a k∈K                                              k∈S finite subset of K. Evidently, l1(K, Ln(E, F)) is a vector lattice under pointwise operations.

We close this section with a result of this note about order continuous operators on CD r ( K, E) -spaces.

Theorem 17. Let K be a compact Hausdorff space without isolated points and F be a Dedekind complete vector lattice. Then L n ( CD 0 ( K,E),F ) is lattice isomorphic to l4K,U n ( E,F )).

C Define ф : L n ^ CD r (K, E ), F ) ^ l ¹ ( K, L n ( E, F )) via ф(G)(k)(e) = G ( x k 0 e) for each G E L n CD ( K,E ) ,F ) , k E K and e E E . Then ф(G)(k) is order bounded, since ф(G ⁺ )(k) and ф ( G ^- )( k ) are order bounded F -valued operators for each G on CD 0 ( K,E ) . If e _a j 0 in E , then X k 0 e _a j 0 in CD 0 ( K, E ) for each k E K . This gives that ф(G)(k)(e _a ) = G ( x k 0 e _a ) is order convergent to 0 so that ф ( G )( k ) E L n ( E,F ) for each G E L n ( CD 0 ( K,E ) ,F ) . Thus ф(G) is a map from K into L n ( E,F ) and ф(G)(k)(e) >  0 whenever e >  0 and G >  0 , i. e., ф ( G )( k ) is positive for all G >  0 .

Now we will show that ф(G) is an element of l ¹ ( K, L n ( E, F )) . Let S be a finite subset of K and G E L n ( CD 0 ( K,E ) ,F ) . Then

X |ф(G)(k)|(|f (k)|) = £ |ф(G+ - G-)(k)|(|f(k)|) k∈Sk

6 ^ф(G+)(k)(|f(k)|) + ^ф(G-)(k)(|f(k)|) k∈Sk

^X χ k ⊗| f | k ∈ S

+ G ^- Ex k 0| f I k ∈ S

= ^G+(xk 0 If |) + X G—(Xk 0 If I) = G+ k∈Sk for each f E CD0 (K, E). Hence we get

X |Ф(О)(к)|(|/(k)|) 6 G+ (If|) + G-(If|) = |G|(|f|) k∈S as ^2 Xk 0 |f | Ts |f |, G+ and G- are order continuous. k∈S

Let e be an arbitrary but fixed element of E+ . Then sup ElФ(G)(k)I(If(k)|) 6 sup |G|(|f|) 6 |G|(e) E F, kfke 61 V                       kf ke61

as |f| 6 kfkee.

So far we have shown that ф(G) satisfies the first condition of Definition 16. Also we have to show that

E |Ф(G)(k)|(fa(k)) ^a 0 k for each fa E CDq(K,E) such that fa ^ 0. It is sufficient to verity the claim for a positive G E Ln(CD0(K,E),F). Let 0 6 G E Ln(CDr(K,E),F) and fa j 0 in CDr(K,E^'. For a fixed α, we have    χk ⊗ fα ↑S fα . Since G is order continuous and positive, we have k∈S

G ( X X k 0 f a j = X G ( X k 0 f a ) T G(f a ). k ∈ S              k ∈ S

Thus

X | ф(G)(k) | (f a (k)) = X ф(G)(k)(f a (k)) = X G ( X k 0 f a ) = G(f a ) I 0. k ∈ K                  k ∈ K                 k ∈ K

Hence the map ф(G) we have defined belongs to l 1 ( K, L ^ ( E, F)) .

It is easy to see that ф is linear. We now show that it is bipositive. Certainly ф(G) > 0 whenever G > 0. Now assume that ф(G) > 0 for some G E Ln(CD0(K,E),F) and take 0 6 f E CD^(K, E). As P Xk 0 f Ts f in CD0(K, E), we have P G(xk 0 f) - G(f). By k∈S                                         k∈S definition, G(xk 0 f) = Ф(G)(k)(f) > 0 and thus G(f) > 0 for each 0 6 f E CD0(K,E), i. e., G > 0. We now show that ф is one-to-one. Let ф(G) = 0 for some G E Ln(CD0(K,E),F). Then G(Xk 0 f) = 0 for each k E K and 0 6 f E CD0(K, E). As G is order continuous and P Xk 0 f Ts f, this gives that 0 = P G(xk 0 f) - G(f) or G(f) = 0. As CD0(K, E) is a k∈S                                    k∈S vector lattice, we get G = 0.

To show that ф is surjective, take an arbitrary 0 6 a E 1 1 ( K,L n ( E,F )) and define G : CD r (K,E) + - F by G(f) = P a(k)(f(k)) . Then G is additive on CD 0 (K, E) and k ∈ K

G ( f ) = G ( f + ) — G ( f ^- ) extends G to CD 0 ( K, E) . We now verify that ф(G) = a . If 0 6 e E E , then

ф(G)(k o )(e) = G(x k o 0 e) = X a(k)(x k o 0 e)(k) = a(k o )e.

k ∈ K

Since e E E is arbitrary, we conclude that ф(G)(k o ) = a(k o ) and k o is arbitrary, we have ф(G) = a . B

Acknowledgement

I would like to thank Prof. A. G. Kusraev as he read this manuscript and made many valuable suggestions and comments on it.