Линейная дифференциальная игра удержания с поломкой

Нарушение динамики в дифференциальных играх преследования-уклонения в числе первых рассмотрел М.С. Никольский [1-4]. Так, в статье [3] используется второй метод Л.С. Понтрягина [5] для построения и -стабильного моста [6, с. 52].

В данной статье будет рассмотрено нарушение динамики в линейной дифференциальной игре удержания. Как и в статье [3], будет рассмотрена разовая поломка у первого игрока, при возникновении которой он обездвижен на некоторое время, данная поломка происходит в заранее неизвестный момент времени. Вектограммами управлений игроков являются n -мерные выпуклые компакты, которые зависят от времени. Поставленная игра удержания будет рассматриваться со стороны первого игрока, которому необходимо удерживать состояние системы в заданном выпуклом терминальном множестве на протяжении всего времени игры, несмотря на возможную поломку и управление второго игрока. Для построения и -стабильного моста используется второй метод Л.С. Понтрягина. Так строится многозначное отображение, которое равно пересечению альтернированных интегралов Л.С. Понтрягина на терминальное множество при фиксированном моменте поломки, пересечение берется по времени поломки и по верхнему пределу интегрирования альтернированного интеграла. Также приводится доказательство, что построенное отображение является и -стабильным мостом для рассматриваемой игры, если выполняется ряд условий. В подтверждение существования в конце статьи будет рассмотрен простой случай на плоскости, где вектограммами управлений игроков являются круги постоянного радиуса с центром в начале координат. В данном примере строится u-стабильный мост по предложенному методу, а также строится экстремальная стратегия [6, с. 57] на данный мост.

В первой части статьи описывается постановка рассматриваемой задачи удержания, во второй части вводится в рассмотрение используемый математический аппарат и строится u-стабильный мост, а в третьей части рассматривается простой пример.

Постановка задачи

Пусть задано выпуклое ограниченное множество M с R", временной отрезок [0, T] и начальный фазовый вектор системы z(0) = z0 е M, тогда если на протяжении t е [0, T] выполнялось включение z(t) е M , то игра заканчивается и побеждает первый игрок, иначе, если в некоторый момент t* е (0, T] данное включение нарушилось, тогда игра заканчивается и побеждает второй игрок.

Положим Ж+={x е!:x> 0} . Для достижения своих целей игроки строят допустимые управления, с помощью которых происходит воздействие на систему. Для упрощения рассуждений вектограммы управлений игроков будут заданы выпуклыми компактами P и Q из Iй, а множитель, зависимый от времени, будет учтен в виде коэффициента. Допустимое управление первого игрока задается функцией u :[0, T] х IR^ ^ P, коэффициент задается интегрируемой функцией a: [0, T] ^ Ж +. В заранее неизвестный момент времени 0 е [0, T] может произойти поломка на время h. Для математического описания поломки введем функцию ф0, которая имеет вид

I 0 t е [ 0 , 0 + h ] ф о ( t ) =L

•

1 1     иначе

Допустимое управление второго игрока задается функцией v :[0, T ] х Ж ^й ^ Q , коэффициент задается интегрируемой функцией b :[0, T ] ^ Ж₊ .

В силу выше сказанного движение системы можно описывать линейным дифференциальным уравнением dz

~ = b(t ) • v ( t , z ( t )) - a(t ) • ф о ( t ) • u ( t , z ( t )), z (0) = z 0 ,   v ( t , z ( t )) е Q , u ( t , z ( t )) е P ,   t е [0, T ]•   (1)

dt

Дадим определение движения системы (1), порожденного допустимыми управлениями игроков из начального положения z ₀ . Возьмем разбиение ю временного отрезка [0, T ] с диаметром d ( ю ) следующим образом:

ю :0 = 1 ₀ <  t 1 < ... <  t m _{+ 1} = T ,   d ( ю ) = max ( L _{+ 1} - L ) .

0< i <  m

Построим ломаную

^Zю ⁽ t ) = ^Zю

Г ₊ A

^(ti ) ^- / ф о ^{( r} ) • a ⁽ r ) dr • ^{u (} t i , ^z® ⁽ t i )) ⁺ J ^{b (} r ) dr • ^{v (} t i , ^z® ⁽ t i )),

V t i

J

V t i          J

при z _ro (t 0 ) = z 0 , t е [ t i , t i ₊ i ] . Семейство ломаных (2) является равномерно ограниченным и равностепенно непрерывным согласно [7, с. 46], а значит, удовлетворяют условию теоремы Арцела [8, с. 104]. Под движением системы (1) с допустимыми управлениями и и v и с начальным условием z(t 0 ) = z 0 понимается любой предел подпоследовательности последовательности ломаных (2), которая равномерно сходится на отрезке [0, T ] при d ( ю ) ^ 0.

Построение стабильного моста

Введем в рассмотрение операции Минковского [5] над множествами.

Определение 1 . Алгебраической суммой непустых множеств A и B из Ж ^л называется множество

A + B = { x е Ж ^л : x = a + b , а е A , b е b } = [J ( A + b ).

Ь е B

Определение 2. Произведением непустого множества A из Жй на число в называется множество в • A = {x е : x = в • а, а е а} .

Определение 3 . Геометрической разностью непустых множеств A и B из ⁿ называется множество

A - B = { x e x " : x + B c a } = A( A - b ).

b e B

Введем в рассмотрение интеграл Ауманна [9, c. 326].

Определение 4. Пусть задано многозначное отображение X :Ж ^ В", значения которого являются непустыми компактами. Интегралом Ауманна от X(1) на отрезке [11,12] называется множество

J X ( r ) dr =

J x ( r ) dr : измеримая x ( r ) e X ( r ) при

почти всех 1 1 <  r <  1 ₂ > .

Лемма 1 [3] . Пусть заданы некоторые непустые множества B , C и задано { A i } - семейство непустых множеств, которые зависят от параметра i e I и пусть 3 j e I : A j = Q A i , тогда ieI

П [(4 + B)-C ] = ie I

A A i + B - C

Введем в рассмотрение альтернированный интеграл Л.С. Понтрягина [5] для рассматриваемой игры. Построим многозначные отображения U _o (1 ) = ф_о (1 ) • a(1) • P и V(1 ) = b(1) • Q при 1 e [0, T ]. Так как значения данных отображений при 1 e [0, T ] - это выпуклые компакты из R " , то данные отображения равномерно ограничены на отрезке [0, T ], то есть

3 r e R : V 1 e [0, T ] ^ U(1 ) c r • 5 , V(1 ) c r • 5 , где S – это n -мерный шар единичного радиуса с центром в начале координат. Возьмем разбиение to отрезка [0, T ]:

^ ^:0 = ¹ 0 <  ¹ ₁ <  ... <  ¹m _{+ 1} = T .

Положим

U i = J U _o ( r ) dr  V i = J v ( r ) dr  i = 1.. m + 1.

4 - 1                         4 - 1

Положим A = M и определим A m _{+ 1} индуктивно

A = ( A i - 1 + U i ) - V i   i = 1... m + 1.

Множество Am+1 называется альтернированной суммой, а пересечение Am+1 по всевозможным разбиениям to отрезка [0, T] называется альтернированным интегралом Л.С. Понтрягина и записывается в виде

T

W o (0, T ) = J [U _e ( r ) - V ( r)]dr .

M ,0

В силу определения имеем, что V 1 e [0, T ] выполняется W ₆ (1 , 1 ) = M .

В следующей лемме представлено ключевое свойство альтернированного интеграла, которое связывает его с u -стабильным мостом.

Лемма 2 [3] . V 1 e [0, T ] и Ve e [0, T - 1 ] выполняется следующее включение:

1+e

1+e

- J V ( r ) dr .

t

W _e ( 1 , T ) c

W _e ( 1 + e , T ) + J U _e ( r ) dr

t

Из данного включения и введённых определений следует, что V z(1) e W6 (1, T), выполняется включение

Л 1 + e

z ^{( 1} ) e A U ^W9 ^{( 1 + e} , ^T ) ⁺ J Ф о ⁽ r ) • a ⁽ r ) dr

• u

—

veQ

ueP

^ 1 + e        A

J b ⁽ r ) dr  • v ,

то есть 3 и* g P, что V v g Q выполняется включение z (t) -

^ t + c                  ^

J Ф е ⁽ r )" a ⁽ r ) dr

V t               J

• и * +

^ t+C         ^

J b ⁽ r ) dr

U    J

• v = z ( t + c ) g W _e (t + c , T )

Введем в рассмотрение понятие и-стабильного моста [6, c. 52]. Пусть начальное состояние системы z(0) g We (0, T), тогда в силу леммы 2 существует допустимое управление первого игрока и(t, z(t)) , что при любом допустимом управлении второго игрока v(t, z(t)) и любом моменте поломки е g [0, T] будет выполняться включение

z(t) g W e (t , T ), t g [0, T ],                                        (3)

а конечное состояние z(T) g W _e (T , T ) = M . Тогда множество { ( t , x ): t g [0, T ], x g W _e (t , T ) } называется и-стабильным мостом для дифференциальной игры преследования-уклонения, заданное дифференциальным уравнением (1) к множеству M . Однако из включения (3) не следует включение z(t ) g M , t g [0, T ], которое требуется от первого игрока в рассматриваемой игре. Чтобы учесть требуемое включение, построим следующие множества:

D e ( t , T) = р| W e (t , s ); D(t , T ) = Q D e (t , T) ;

s g [ t ,T ]                                 e e [ t ,T ]

B _e = { (t,x ): t g [0, T ], x g D _e ( t , T ) } ; B = { ( t , x ): t g [0, T ], x g D(t , T ) } .

Лемма 3 . При V t g [ 0, T ] , если D (t , T ) ^0 , то выполняется включение D (t , T ) c M и D _e ( t , T ) c M при e e [ t , T ].

Доказательство. Пусть t g[0, T], D(t, T) ^0. Множество D(t, T) согласно определению рав- но

D(t , T ) = p| D e (t , T ),                                     (4)

e e[ t , T ]

а каждое D _e ( t , T ) согласно определению равно

D e ( t , T ) = p| W e ( t , s ).                                      (5)

S G[ t ,T ]

При V e e [ t , T ] в пересечении из (5) присутствует элемент W _e (t , t ) = M , а значит, данное пересечение лежит в M или равно ему, получили, что D _e (t , T ) с M . Так как при V e e [ t , T ] выполнено включение D _e ( t , T ) с M , то пересечение из (4) лежит в M или равно ему, получили, что D(t , T ) с M .                                                                          □

Теорема 1. Пусть начальное состояние игры z0 g D(0, T) и D(t, T) ^0 при t g[0, T]. Пусть V t g [0, T] 3 e g [t, T] такое, что имеет место равенство р| De(t,T) = De-(t,T),                                    (6)

e e[ t , t ]

и V t g [0, T ] 3 s ' g [ t , T ] такое, что имеет место равенство

Р| W e ( t , s ) = W e ( t , s )                                   (7)

S G[ t , T ]

Тогда в рассматриваемой игре удержания первый игрок сможет победить при любом допустимом управлении второго игрока и любом моменте поломки e g [0, T ].

Доказательство. Дано z ₀ g D (0, T ) и D ( t , T ) ^0 при t g [0, T ]. Распишем множество D (t , T ) по определению, получим

D ( t , T ) = p| D e ( t , T ).                                      (8)

e e [ t ,T ]

Рассмотрим отдельно множество D _e ( t , T ), распишем его по определению

D e (t , T ) = p| W e (t , s ).                                        (9)

s g [ t ,T ]

Ослабим пересечение в правой части (9) следующим образом: возьмем некоторое £ е (0, T - t ] и перейдем от [ t , T ] к [ t + £ , T ], затем используем лемму 2, получим, что правая часть (9) лежит в

Q     W ₆ (t + £ , 5 ) + J U ₆ (r ) dr - J V(r ) dr

Так как по условию теоремы выполняется равенство (7), то применим лемму 1 к (10), а полу- ченное пересечение Q  W6 (t + £, 5) заменим, согласно определению, на D6 (t + £, T), получим

5 е[ t+£,T ]

(10) = D ₆ ( t + £ , T ) + J U ₆ ( r ) dr - J V ( r ) dr .

_                         t                J t

Получили, что Vt е[0,T] и V£е[0,T - t] выполняется включение t+£

D ₆ ( t , T ) c D ₆ ( t + £ , T ) + J U ₆ ( r ) dr - J V ( r ) dr .

Аналогично выводам из леммы 2 из включения (11) следует, что множество B ₆ = { ( t , x ): t е [0, T ], x е D ₆ ( t , T ) } является u -стабильным мостом к рассматриваемой игре при фиксированном моменте поломки 6 е [0, T ].

Применим включение (11) к (8), получим

(8) c П D 6 ( t + £ , T ) + J U 6 ( r ) dr - J V ( r ) dr .

6 е [ t ,T ]

Ослабим пересечение в (12) следующим образом: возьмем некоторое £ е (0, T - 1 ] и перейдем от [ t , T ] к [ t + £ , T ], так как по условию теоремы выполняется равенство (6), то применим лемму 1, а полученное пересечение Q D ₆ ( t + £ , T ) заменим, согласно определению, на D (t + £ , T ),

6 е [ t , T ]

получим, что правая часть (12) лежит в

D ( t + £ , T ) + J U ₆ ( r ) dr - J V ( r ) dr .

_                       t                J t

В итоге получили, что V t е [0, T ] и V £ е [0, T - 1 ] выполняется включение

D(t , T ) c D ( t + £ , T ) + J U ₆ ( r ) dr - J V ( r ) dr .

Аналогично из включения (13) следует, что множество B = { ( t , x ): t е [0, T ], x е D (t , T ) } является u -стабильным мостом к рассматриваемой игре.

Теперь опишем алгоритм движения первого игрока для достижения победы. Поскольку z ₀ е D (0, T ), то (0, z ₀) е B . Так как B - u -стабильный мост, то существует такое допустимое управление и 1 , что при любом допустимом управлении второго игрока движение системы z ( t ) удовлетворяет включению

z(t ) е D(t , T ), t е [0, T ].

Например, можно положить u 1 = u f - экстремальная стратегия [6, с. 57] к B , тогда в силу леммы 15.1 из [6, с. 62] включение (14) будет выполняться. Если поломка не происходит, тогда в силу леммы 3 и включения (14) выполняется включение z(t ) е M при t е [0, T ], то есть игра закончится в момент времени T и первый игрок победит.

Иначе, если поломка произошла в момент 6 е [0, T ], тогда первый игрок в момент времени 6 ' останавливается и устраняет поломку в течение времени h ' = min( T - 6 ’, h ), после чего продолжает движение. Из включения (14) следует, что в момент поломки выполняется включение

z ( O ’) g D ( O ’, T ) , а согласно определению множества D ( O ’, T ) следует включение z( O ) g D _o ( O ', T ) , из которого в свою очередь следует включение ( O ', z( O ')) g B _o . Так как B _O - u -стабильный мост, то при любом допустимом управлении первого игрока (любом, так как функция поломки ф_о (t ) = 0 при t g^O ', O ' + h ' ] ) и любом допустимом управлении второго игрока движение системы z ( t ) удовлетворяет включению

z(t ) g D _o (t , T ), t g [ O ', O ' + h ']. (15)

Тогда в силу леммы 3 и включения (15) выполняется включение z(t ) g M при t g\O ', O ' + h '], то есть пока первый игрок устраняет поломку, второму игроку никак не удастся нарушить включение z(t ) g M . Через время h ' первый игрок продолжает движение, а фазовый вектор системы z( O ' + h ') g D _o ( O ' + h\ T ) , то ( O ’+ h\ z( O ' + h ')) g B _o . Так как B _o - u -стабильный мост, то существует такое допустимое управление u , что при любом допустимом управлении второго игрока, движение системы z ( t ) удовлетворяет включению

z(t ) g D _o (t , T ), t g [ O ' + h\T ]. (16)

Например, можно положить, u2 = ue - экстремальная стратегия [6, с. 57] к Во , тогда в силу леммы 15.1 из [6, с. 62] включение (16) будет выполняться. Тогда в силу леммы 3 и включения (16) выполняется включение z(t) gM при t g\O' + h',T], то есть игра закончится в момент време ни T и первый игрок победит, несмотря на поломку в момент времени O’.                   □

Пример. Пусть задано число m > 0 и множество M = m • S, положим, a(t) = amax , b(t) = bmax при t g[0, T], причем amax > bmax. Альтернированный интеграл Wo (t, T) при t g[0, T], согласно теореме из [10], равен m + a max (T - t - h) - bmax (T - t)

t <  O <  O + h <  T t <  O <  T <  O + h O <  t <  O + h <  T , O <  t <  T <  O + h

O + h <  t <  T

W o ( t , T ) = S •

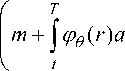
- b max dr = S 4

^{m + a} max ^{( O} - t ) - ^b max ^{( T} - t ) m + a max ( T - O - h ) - b max ( T - 1 ) ^{m -} b max ^{( T -} t )

. ^{m + a} max ^{( T -} t ) ^{- b} max ^{( T -} t )

причем W _o ( t , T ) ^ 0 , если выполняется следующее неравенство

T m ^ max f (bmax - Фо (r) • amax ) dr • t

T

Чтобы данное неравенство выполнялось для всех моментов поломки, возьмем максимум по времени поломки, получим

T m > max max f (bmax - Фо (r) ' amax ) dr = bmaxh .                       (17)

t<T^J

T

Отсюда множества D(t, T) и D_O (t, T) при t g[0, T] и Og[0, T] равны

m

t< O -

bmax ^{h a} max  bmax

< O< O + h< T

Do (t, T) = S '^

^{m + a}max^{(O -}t) ^{- b}max^{(O + h -}t)

m m - bmax(O + h - t) m - bmax(T - t)

m

b h

O--bmaxj— < t < о < о + h < T amax - bmax t < O < T < O + h

O< t< O + h< T

O< t< T< O + h

O + h< t< T

D(t, T) = S • (m - bmax min [T -1, h]).

Из неравенства (17) следует, что если m > hbmax, тогда D9 (t, T) и D(t, T) при t e[0, T] и 9 e [0, T] являются непустыми множествами, тогда первый игрок может построить экстремаль- ные стратегии uf, uf, которые согласно [6, с. 62] равны

Vu(t) G 5  ||z(t)|| < m - hbmax ue (t, z (t)) = ‘

z(t)        ii / xii           ,,      , t e[0,9'],

P(t)i    ||z⁽t )|| > ^{m -}hbmax

V u (t) e 5 z(t) < m u e(t, z(t))=^ z (t) [  lz (11 z(t) > m ’ t e[9'+ h',T], где 9' - момент поломки (если поломки не было, то 9 = T), а время починки равно h' = min(T - 9', h). При использовании пары управления и = ( uf, и2 ) первый игрок сможет дос- тигнуть цели при любом допустимом управлении второго игрока и любом моменте поломки согласно теореме 1. Условия теоремы (6) и (7) очевидным образом выполняются для рассматриваемого примера, поскольку пересечение кругов с центром в начале координат равняется кругу с минимальным радиусом.

Автор выражает благодарность своему научному руководителю Ухоботову Виктору Ивановичу, доктору физ.-мат. наук, зав. кафедрой теории управления и оптимизации ЧелГУ, за значимые замечания и важнейшие советы при проведении исследования и оформлении данной ста- тьи.