ЛИНЕЙНАЯ ИОННАЯ ЛОВУШКА С ОСТРОВОМ СТАБИЛЬНОСТИ, ФОРМИРУЕМЫМ КВАДРУПОЛЬНЫМ ВОЗБУЖДЕНИЕМ

Резонансное квадрупольное возбуждение колебаний ионов в квадрупольном фильтре масс (КФМ) вызывает появление полос нестабильности на a–q диаграмме Матье, следующих вдоль изолиний параметра β [1, 2]. Параметр β зависит от координаты ( a , q ) и определяет спектр колебаний ионов в квадрупольном электрическом поле [3]. Уравнения движения ионов при наличии дополнительного квадрупольного напряжения V a = = V x cos ωt имеют вид [2]

d ² x d ξ ²

-[ a - 2 q cos ( 2 ( ^ - ^ 0 ) ) - 2 q x cos2 v^ J x ,

d^y = +[a - 2qcos(2(^ - ^))- 2qx cos2v^ ly,

где a и q — параметры уравнения Матье, определяемые, как

8 eU      _

( m / z ) Q ² r ₀ ² , q ( m / z ) ^ ² r ₀ ² ,

4eVω x-     , V _

(m / z) a2 r02

Здесь x и y –поперечные координаты квадрупольного фильтра масс (КФМ), ±( U + + V cosΩ t + V x cos ωt ) — напряжение, прикладываемое к электродам КФМ, ze — заряд иона, r 0 — радиус вписанной окружности между вершинами электродов.

Цель настоящей работы состоит в изучении ионно-оптических свойств острова стабильности по оси q, создаваемого квадрупольным возбуждением на частоте ν = 0.5. Это означает, что, если частота основного напряжения равна 2 МГц, то частота дополнительного квадрупольного напряжения составляет 1 МГц. В частности, работа включает расчет положения острова стабильности в функции от амплитуды qx и частоты ν, определение параметра β и глубины потенциальной ямы в зависимости от положения рабочей точки q, на основе этого моделирование контура пропускания КФМ и контура возбуждения при масс-селективном выбросе ионов из ловушки на границе стабильности.

ДИАГРАММА СТАБИЛЬНОСТИ

На рис. 1 показана модифицированная диаграмма стабильности КФМ при квадрупольном возбуждении с безразмерной амплитудой q x = 0.01 и q x = 0.1. Поскольку частота резонансного возбуждения ν = 0.5, полосы нестабильности следуют вдоль изолиний β_x = β_y = 0.5. С увеличением амплитуды q x ширина полосы нестабильности возрастает — на порядок при q x = 0.1, при этом размеры острова стабильности (В), расположенного по оси q , уменьшаются. Нас интересует интервал стабильности по оси q при a = 0.

Метод построения диаграммы стабильности (рис. 1) заключается в задании прямоугольной сетки на a–q плоскости. В заданных узлах сетки ( a i , q i ) рассчитывалась матрица M преобразования координат и скоростей, как и в случае уравнения Матье [3, 4]. Элементы матрицы M рассчитываются численным интегрированием уравнений (1) и (2) при начальных условиях: (a) u 0 = 0, u 0 ' = 1

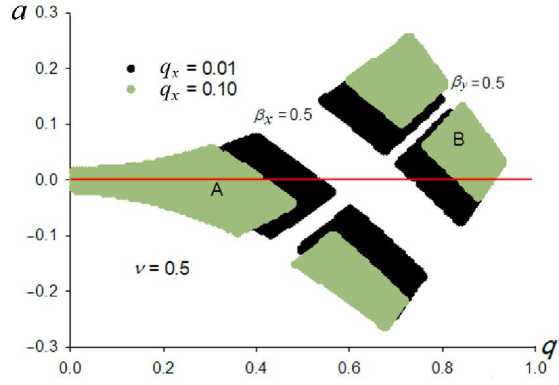
Рис. 1. Острова стабильности (А, В).

При параметрах квадрупольного возбуждения: частота ν = = 0.5, амплитуды q x = 0.01 и q x = 0.1; параметры стабильности β x = β y = 0.5

и (b) u 0 = 1, u 0 ' = 0. Здесь u = x или y . В нашем случае уравнения движения (1) и (2) — это уравнения Хилла. Поэтому интегрирование осуществлялось на интервале (0, 2π), поскольку функции 2 q· cos[2( ξ – ξ 0 )] и 2 q x ·cos2 νξ имеют наименьший общий период 2π. Если след матрицы

РЕЗУЛЬТАТЫ

На рис. 2 представлен в деталях остров стабильности при параметре возбуждения q x = 0.1 и частоте ν = 0.5.

Интервал стабильности ( q 1 , q 2 ) по оси q при a = = 0 контролируется амплитудой возбуждения q x . Это иллюстрируется на рис. 2. Из рис. 1 видно, что при увеличении q x полоса пропускания ( q 1 , q 2 ) уменьшается. Однако режим сепарации только в высокочастотном (ВЧ) режиме в этом острове стабильности практически невозможен, поскольку первый остров стабильности вблизи начала координат "затеняет" рабочий остров B (рис. 1). Это означает, что масс-спектры от островов будут накладываться.

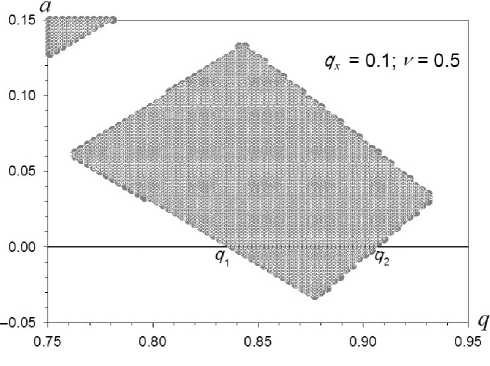
Рис. 2. Остров стабильности B.

При a = 0 в интервале ( q 1 , q 2 ) c амплитудой возбуждения q x = 0.1 и частотой ν = 0.5

На рис. 3 приведены зависимости [6] частотных параметров β x и β y от параметра Матье q для острова B ( a = 0). Эти зависимости показывают, что частотный спектр колебаний ионов по X и Y координатам отличается. В области совместной стабильности по двум координатам, отмеченной пунктирными вертикальными линиями, колебания ионов по X лежат в низкочастотной области, а по Y — в высокочастотной.

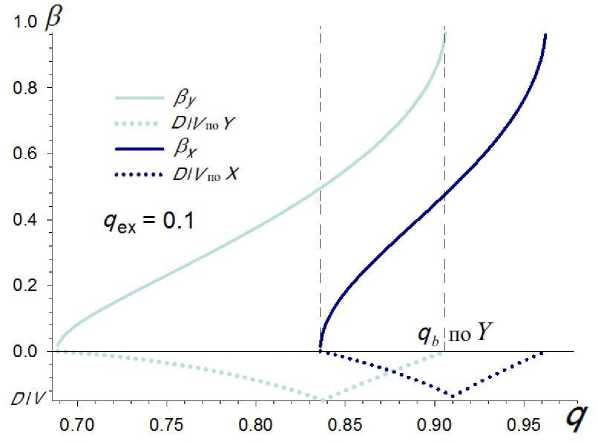
Рис. 3. Зависимости параметров β_x и β_y от параметра q и глубины потенциальной ямы D / V для X и Y поперечных координат при a = 0.

Также на рис. 3 приведены зависимости глубины D / V потенциальной ямы квадрупольного поля [7] для модели, предложенной в работе [8]. В центре области стабильности одновременная глубина достигает максимума. Важно отметить, что максимум глубины потенциальной ямы достигает наибольшей величины по координате X при значении qb, когда по Y координате величина q достига- ет границы стабильности. Это может служить основанием реализации масс-селективного выброса ионов через Y стержни при достижении границы qb (рис. 3) [6, 9].

На рис. 4 иллюстрируется масс-селективность резонансного выброса на границе q b = 0.9064 ( q x = = 0.1) и на границе q b = 0.9082 ( q x = 0.01).

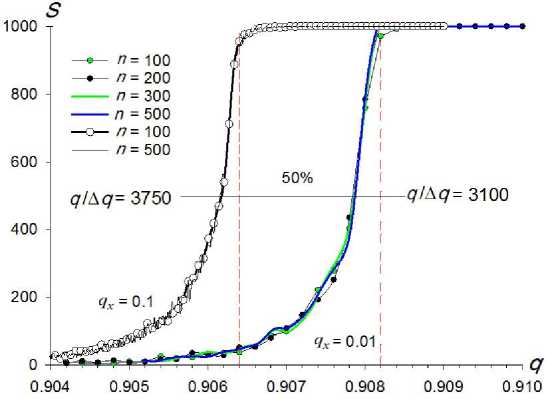
Рис. 4. Зависимости числа ионов S , достигших поверхности электродов Y , от параметра q.

Для двух значений амплитуды квадрупольного возбуждения q x = 0.01 и q x = 0.1; n — число периодов интегрирования уравнений движения в точке q

Построение зависимостей S ( q ) производилось следующим образом. В точке q вблизи границы рассчитывалось 1000 траекторий на интервале (0, n π) и определялось число S траекторий, амплитуда которых превышала r ₀. Количественно масс-селективность можно определить как отношение q b к полосе Δ q по 50% уровню числа выброшенных ионов из ловушки. Величина q b /Δ q составляет порядка 3000 и слабо зависит от скорости сканирования f / n , где f = Ω / 2π — частота ВЧ-генератора, n — число периодов интегрирования. Контур возбуждения T ( q ) трансформируется краевыми полями электрода и входными полями детектора в массовый пик.

Последовательный выброс ионов по массам из ловушки достигается увеличением амплитуды V ВЧ-генератора. Из формул (3) следует, что

V = qx-v = —0.1- V = 0.1103 V для q_x = 0.1

x qb     0.9064                   x и Vx = 0.01103V для qx = 0.01.

Второй случай ( q x = 0.01) более предпочтителен, поскольку требуемая амплитуда V x дополнительного квадрупольного напряжения [10, 11] на порядок меньше, а массовая емкость ловушки больше и составляет

M 2 = q 2 . 0.91 = 1.4.

M ₁ q ₁ 0.65   ..

При амплитудной развертке по шкале масс отношение V_x / V должно быть постоянным. Так, при амплитуде V = 2000 В максимальная амплитуда добавочного напряжения равна 22 В.

ЗАКЛЮЧЕНИЕ

В работе описаны острова стабильности по оси q , формируемые дополнительным квадрупольным напряжением [12–15] с частотой ω = 0.5 Ω. На данной частоте первая область стабильности КФМ расщепляется на четыре острова, причем два из них пересекают ось а = 0. Показано, что существуют благоприятные условия, при которых в острове B в случае а = 0 происходит масс-селек-тивный выброс ионов на Y границе, что одновременно соответствует максимуму глубины потенциальной ямы по X координате. В этом режиме достигается масс-селективность q b / Δ q ≈ 3000. Требуется малая величина дополнительного квадрупольного напряжения порядка нескольких десятков вольт, что упрощает схему формирования дополнительного квадрупольного напряжения на электродах фильтра масс.