Линейно поляризованное поле плоской апертуры

Апертурные антенны широко используются для различных инженерных решений, в первую очередь для спутниковой связи, например параболические излучатели. Основным преимуществом таких антенн является высокий коэффициент усиления, который достигается за счет большого отношения размера антенны к максимальной длине волны используемого сигнала [1].

Хотя поля узкополосных антенн были изучены и описаны 50–70 лет назад, из-за громоздких расчетов с использованием монохроматических сигналов все еще обсуждается большое количество вопросов, например критерий дальнего поля. Также неопределенности существуют в выборе таких параметров измерений диаграммы направленности в ближней зоне, как расстояние апертура – зонд, размер области сканирования и т. д.

ЭМ-поля импульсных сигналов апертурных антенн [2] становятся актуальными для исследований в связи с постоянным расширением полосы рабочих частот систем связи. Для расчета поля апертурной антенны на монохроматическом (узкополосном) сигнале обычно используется либо апертурный, либо токовый метод расчета поля [1–5].

Метод физической оптики во временной области, в котором на поверхности рассеивателя определяется контур интегрирования, используется в [6–18]. Аналогом метода физической оптики во временной области является апертурный метод [19–24].

В апертурном методе элемент Гюйгенса часто используется в качестве элемента апертуры. Нормированная амплитудные диаграмма направленности антенны элемента Гюйгенса определяется выражением

а ( ^f , f a ) = ( 1 + cos ( y ) ) / 2.

Здесь ^f - радиус-вектор от точки апертуры r a до точки наблюдения; у - угол между нормалью к поверхности и направлением на точку наблюдения. Однако такая диаграмма направленности действительна только для компонентов поля в свободном пространстве. Существуют другие представления диаграммы направленности антенны элементарного излучателя а ( ^f , ^f a ) для разных задач. Иногда этот множитель может быть выражен как cos ( у ) [4].

В теории апертурных антенн [1–6] предполагается, что ток на поверхности металла J e равен f e = 2 1^ й , H s ] , где й - вектор нормали к апертуре, а H l s - магнитное поле на поверхности апертуры. Следует отметить, что это выражение верно, если поверхность апертуры идеально проводящая и имеет бесконечные размеры.

Элемент поверхности апертуры S можно рассматривать как элементарный электрический излучатель (элементарный диполь), если магнитные силовые линии действуют по касательной к нему, тогда как тангенциальные электрические силовые линии отсутствуют. Таким образом, его можно рассматривать как элемент длинного про

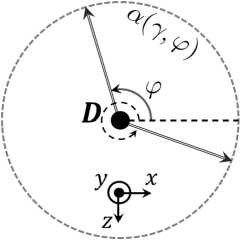
а

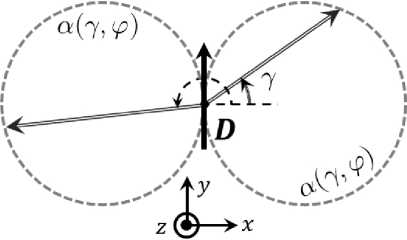
б

Рис. 1. Диаграмма направленности электрического диполя в горизонтальной ( а ) и вертикальной ( б ) плоскостях

Fig. 1. Directional pattern of an electric dipole in the horizontal ( a ) and vertical ( b ) planes

вода с бесконечной проводимостью. Линейный размер I элемента должен удовлетворять условию l « X . Согласно граничным условиям при переходе «идеальный проводник (провод) – свободное

импульсной характеристики (ПИХ) E ( г , t ) в точке ⁷ может быть получена в следующем виде [6]:

пространство», тангенциальная составляющая вектора E будет равна нулю, а тангенциальная составляющая вектора H определяется значением поверхностной плотности тока.

Пространственная нормированная амплитуд-

E ( 7 , t ) = — IT

2 п c   S a

g ( 7a )a( 7,7a ^ t -

1⁷ — ⁷ a l

M ] c

-------^ dS a .     (2)

ная диаграмма направленности элементарного

электрического диполя, представленная в виде

некоторой функциональной поверхности F ( у , ф ) ,

представляет собой трехмерную фигуру. На прак-

тике обычно используют плоские амплитудные диаграммы направленности, изображающие за-

висимость значений напряженности поля от направления в одной из двух основных плоскостей (рис. 1).

1. Основные уравнения

Из апертурной теории, основанной на физической оптике, известно, что передаточная функция

апертуры с равномерным распределением поля может быть найдена с использованием простран-

ственно-частотной зависимости поля излучателя

от определенной поляризации [1]:

E ( 7 , ю ) =

2 п c   S a

g ( a )^a( ^{7 7}q ) e ^Ю r a / °

1 ⁷ - 7 . 1

dS a .

Здесь ю - круговая частота; c - скорость света; S a - поверхность апертуры; g ( 7 ) — функция освещенности апертуры; а ( г , 7 ) — поляризационный множитель, который определяется диаграммой направленности элементарного излучателя

Поэтому если используется принятая нами идеализация, то такая форма является представлением поля, в то время как излучаемый сигнал представляет собой δ-импульс. Поскольку в действительности поле апертуры пропорционально частной производной входного тока по времени, во многих случаях удобнее работать с производной от первообразной (импульсной характеристики), так как это проще и нагляднее.

Будем считать, что энергия импульсного сигнала Sin (t) сосредоточена в основном в полосе частот ю « ю « ю и X   « D, где D - диа- mini           max     imax метр круглой апертуры; или Xmax ^ 2R, где R - радиус апертуры. Хотя выражение (2) было бы формально неверно, но в данном случае это позволит нам получить правильный результат для сигнала на входе антенны Sin (t) (подробнее см. [3] и [6]).

Таким образом, это наиболее удобные ход вычисления представления поля излучаемого δ-импульса, затем производной ПИХ и, наконец, вычисления свертки ИХ и входного импульса по формуле (3).

В результате, используя (2) и с заданным сигналом на входе антенны S in ( t ) , можно получить выражение для поля в любой точке перед апертурой, учитывая предположение, что вся система линейна [6]:

апертуры.

Для сверхширокополосных импульсных сигналов удобнее работать с временным представлением сигнала. Как показано в [6], можно пред-

^SE ( ⁷ - 1 ) = S in ( t ) ®^ ^E ^ = S in ( t ) ® ^h ( ⁷- t ) •

положить, что каждая точка апертуры излучала

5-импульс в момент времени t = 0 . Первообразная

Здесь _Е ( ⁷ , t ) - первообразная импульсной характеристики; функция h ( ⁷ , t ) - ИХ апертуры; символ ® - означает свертку по времени. В [6] было показано, что _Е ( ⁷ , t ) может быть выражено как

а

б

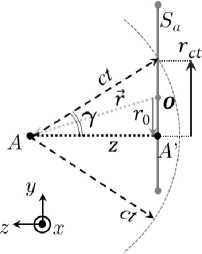
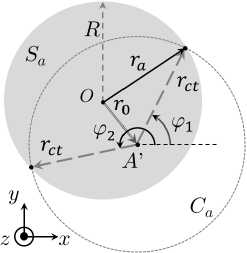
Рис. 2. Апертура S a и воображаемая сфера с радиусом ct ( а ); апертура S a , контур интегрирования C a и угол ф ( б ) Fig. 2. Aperture S a and imaginary sphere with radius ct ( a ); aperture S a , integration contour C a and angle ф ( b )

1                 ■

E ( r ’ t )= 2П J g (ra G Ca M r ’ ra G Ca ) dФ"             (4)

Ф 1

Здесь ^— - радиус-вектор от точки на апертуре —₁ до точки наблюдения A (рис. 2, a ), контур C_a представляет собой окружность с радиусом r_ct = ^( ct ) 2 - z ² ) (рис. 2, б ) с центром в ^— ₀ , где * 0 - проекция вектора г на плоскость апертуры; t - время. Интеграл берется по углу ф , который описывает дугу окружности C_a с центром в 7 0 . Пределы интегрирования ф 1 , ф 2 зависят от положения г таким образом, что оба значения могут варьироваться от 0 до 2π. Предположим, что

Следовательно, во временной области должно быть найдено выражение множителя a ( у ( t ) , ф ( t ) ) , которое позволит описать правильное изменение значения E ( ^— , t ) . Известно, что диаграмма

направленности элементарного электрического диполя в пространственной форме представляет собой круглый тор с центром в середине диполя и равными внутренним и внешним радиусами. На рис. 3 показан диполь и его диаграмма направленности в трех измерениях. Допустим, что напряженность поля E коллинеарна оси у .

Здесь следует отметить, что при расчете интеграла (6) множитель поляризации a нельзя выне-

распределение амплитуды апертуры является постоянным по всей плоскости апертуры g ( ^— _a ) = 1. Перепишем множитель поляризации или зависимость диаграммы направленности апертурного

сти из-под интеграла, так как для каждого угла ф в процессе интегрирования фактически необходимо учитывать значение диаграммы направленно-

сти антенны на участке тора вдоль определенного

элементарного излучателя a ( ^— , —₁) углов у и ф :

а(—,a ) = а(?(—,a ),ф(—a ))•

как функцию

Для первообразной импульсной характеристики следует интеграл:

1 ф 2

6 ( ^— , t ) = 2 n f ^a(^{Y ,} ф ) d ф .

ф 1

Простое выражение для γ можно получить из рис. 2:

cos ( y ) = z I ct .                                              (7)

Как было описано выше, cos ( y ) =a ( y ,0 ) представляет собой диаграмму направленности вер-

тикально расположенного элементарного диполя (или диаграмму направленности элементарного

излучателя плоской металлической поверхности

бесконечной проводимости) в вертикальной пло-

скости (рис. 1). В горизонтальной плоскости диа-

грамма такого излучателя постоянна: a

( 0, ф ) = 1.

направления ( у , ф ) . Это действие обусловлено тем,

*

что радиус-вектор r_ct и, соответственно, попереч-

ное сечение диаграммы направленности каждого

вертикального диполя поворачивается относительно вертикальной оси y при прохождении различных значений угла ф . Следовательно, в каждой точке дуги C_a множитель поляризации имеет

разную величину, поскольку он описывает длину

радиуса сечения тора в направлении угла у . На

рис. 3 предполагается, что операция интеграции выполняется в первой четверти плоскости YOX .

На рис. 4 показаны относительные положения круглой апертуры S_a , контура интегрирования C_a и различных диаграмм направленности a ( у , ф ) в зависимости от угла интегрирования ф .

Следует отметить, что поперечное сечение круглого тора с плоскостью, параллельной его оси вращения, хорошо известно и изучено [8]. Такие сечения представляют собой кривые Персея или овалы Кассини. Каноническое уравнение тора с осью симметрии y выглядит следующим образом:

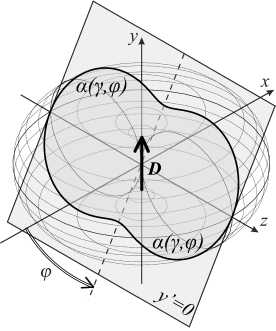
Рис. 3. Диполь D и его диаграмма направленности в трех измерениях

Fig. 3. Dipole D and its radiation pattern in three dimensions

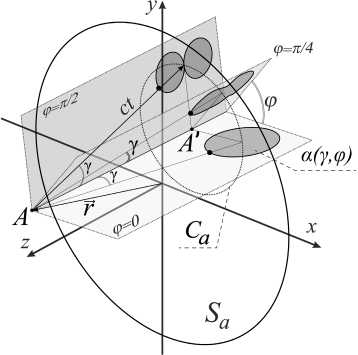
Рис. 4. Круглая апертура Sa, контур Ca и различные диаграм мы направленности a(Y, ф) в зависимости от угла интегрирования ф

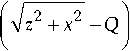
2    2

= y + q ,

Fig. 4. Circular aperture S a , contour C a and different radiation patterns q ( y , ф ) depending on the angle of integration ф

где x , y , z – декартовы координаты; Q – расстояние от оси симметрии на формирование круга (в центре фигуры вращения); Q – радиус образующего круга (фигуры вращения). Каноническое уравнение секущей плоскости:

y = tan ( ф ) x , z = Vg R . (9)

После некоторых перестановок и преобразований можно получить выражение для радиуса поперечного сечения:

r_s = a ( y , ф ) = V 1 - sin ² Y sin ² ф . (10) Заменив y из (7), можно записать как:

a ( t , ф ) = /1 -[ 1 - ( z / ct ) 2 1 sin ² ( ф ) .

Выражение (11) является новым выражением для поляризационного множителя элементарного излучателя металлической плоской поверхности с бесконечной проводимостью во временной области. Отметим, что (11) относится к металлической плоской апертуре независимо от ее формы.

Выражение (6) для первообразной импульсной характеристики с учетом множителя поляризации (11) переписывается следующим образом:

sin ² ( ф ) d ф .

фИ   V       2

Если ввести параметр в = 1 / ^ 1 - ( z / ct ) 2 ^ , теграл (12) можно преобразовать в

1 ф2 ,_________________

E(?’t) = 2^1^в —sin2(ф)dф ф то ин-

У 2p+cos (2ф)-1

У 2 p + cos ( 2 ф ) - 1 / b

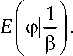
Здесь E ( ф 11 / p ) - эллиптический интеграл второго рода с параметром 1 / р . Этот интеграл является табличным интегралом и не может быть выражен в виде элементарных функций. Такие интегралы были впервые изучены Джулио Фаньяно и Леонардом Эйлером в середине XVIII века [25]. Второй род эллиптического интеграла дает длину дуги эллипса. Эллиптические интегралы как первого, так и второго рода доступны для расчета в Matlab. В общем случае выражение (13) может использоваться для плоской апертуры любой формы. В каждый момент времени t углы интегрирования ф 1 и ф 2 вдоль части окружности C_a определяются точками, в которых этот контур пересекается с границей апертуры S a . Отметим, что в некоторых случаях, таких как прямоугольная апертура, на линии интегрирования может быть несколько таких сегментов (см. [10]), тогда интеграл будет состоять из суммы интегралов по этим сегментам.

• 2. Результаты расчетов

Произведем сравнение результатов расчета временных зависимостей поля, полученных с использованием предложенного метода расчета для трех различных множителей поляризации, и результатов численного моделирования с использованием метода конечного интегрирования (Finite Integration Technique, FIT).

Вычисления в модели производились в пределах счетного объема. Расстояние от поверхности

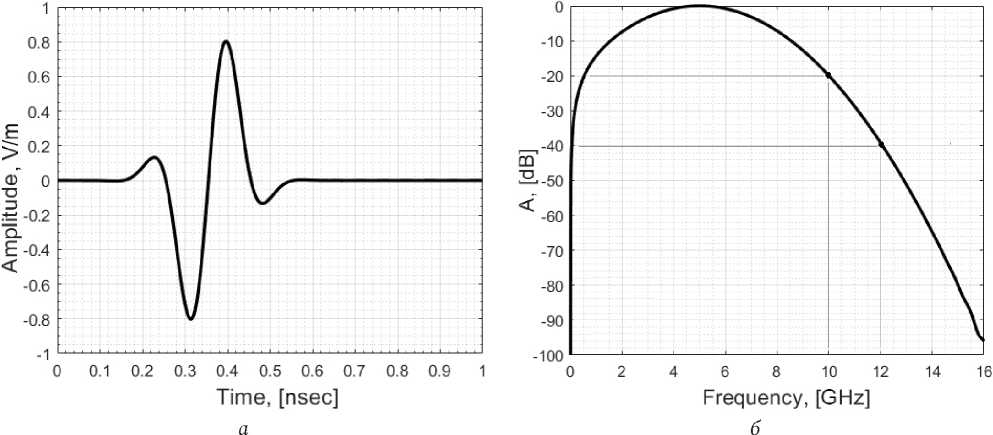
Рис. 5. Биполярный гауссовский UWB-сигнал ( а ); спектр этого сигнала ( б )

Fig. 5. Bipolar Gaussian UWB signal ( a ); spectrum of this signal ( b )

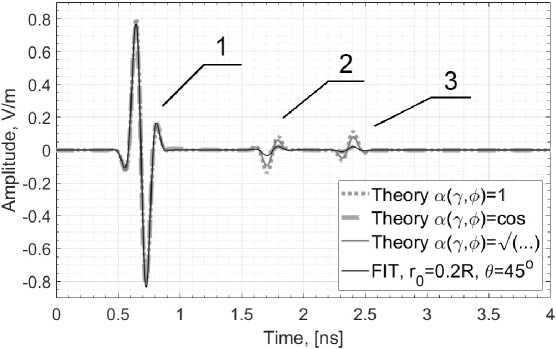
Рис. 6. Сигналы на зондах, полученные численно с помощью FIT (тонкая черная сплошная линия) и свертки с теоретическими

IRF для трех различных а ( у , ф )

Fig. 6. Probe signals obtained numerically with FIT (thin black solid line) and convolution with theoretical IRFs for three different а (у , ф )

апертуры до границ вдоль оси X и оси Y составляло 0,5 метра. Коэффициент отражения согласованных слоев на границах (perfect matched layers) составлял 10 - 5 . Количество ячеек шестигранной сетки, на которые был разделен расчетный объем, было 200 миллионов в четвертой части объема. Использовалось адаптивное формирование сетки: в окрестности неоднородностей структуры создавались более мелкие ячейки.

Линейно поляризованная плоская волна распространялась от границы счетного объема перпендикулярно круглой апертуре. Нулевым моментом времени анализа считался момент отражения от плоской круглой пластины. Перед такой квазиапертурой помещались бесконечно малые линейно поляризованные зонды поля.

В связи с необходимостью ограничения полосы частот в методе FIT для возбуждения плоской волны в моделировании использовался биполярный гауссовский сверхширокополосный (СШП) ультракороткий импульс (рис. 5, a ) со спектром от 1 МГц до 10 ГГц по уровню –20 дБ и до 12 ГГц по уровню –40 дБ (рис. 5, б ).

Сигнал на зонде, полученный численно (пунктирная линия), и свертки входного сигнала (рис. 5, а ) с тремя теоретическими ИХ, производными от выражения (13) для различных множителей поляризации, показаны на рис. 6 и 7.

Зонд расположен в точке г ₀ = 0,2 R , z = 0,2 R , 9 = п / 4. Здесь r ₀ , z , 9 - цилиндрические координаты; 1q - расстояние от оси z ; 9 - угол от оси x . Первый импульс на рис. 6 и 7 является основным

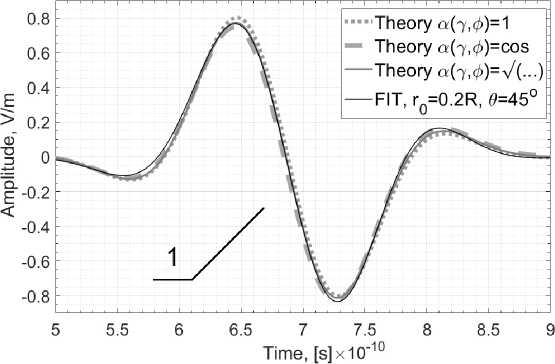
Рис. 7. Сигналы на зондах, полученные численно с помощью FIT (тонкая черная сплошная линия) и свертки с теоретическими

IRF для трех различных а ( у , ф )

Fig. 7. Probe signals obtained numerically with FIT (thin black solid line) and convolution with theoretical IRFs for three different а (у , ф )

импульсом, 2-й и 3-й импульсы на рис. 6 вызваны граничными и краевыми эффектами [6].

На рис. 7 показан увеличенный вид основного импульса, представленного на рис. 6. Здесь видно, что основная форма импульса практически одинакова для всех поляризационных множителей, что говорит об импульсе основной волны. Однако его максимальная амплитуда и время пересечения нуля в середине (приблизительно 6,9 нс) различны. Разница по максимальной амплитуде импульса, полученного методом FIT, и импульса, вычисляемого по формуле (11), составляет около 0,5 %, для «косинусного» поляризационного множителя эта разница будет около 2,5 %, а для изотропного излучателя – около 4 %.

На оси z , когда 1 q = 0, можно наблюдать только два импульса: основной импульс и сумму граничных и краевых эффектов, которые одновременно попадают в эту точку из круглой апертуры. В любых других случаях внутри апертурного или прожекторного луча, когда 1q ^ 0, сигнал от апертуры будет иметь три импульса. При рассмотрении точки за пределами прожекторного луча будут наблюдаться два граничных импульса с противоположным знаком – от ближайшей границы и от противоположного края.

Сравнение сигналов, рассчитанных методом FIT, и предложенным в работе методом показало, что амплитуды второго и третьего импульсов, соответствующих задней части первообразной ИХ, различны. Самая большая разница наблюдается вблизи оси z . Эти отклонения определяются и объясняются диаграммой направленности антенны элементарного излучателя и эффектом, связанным с затеканием токов на границе апертуры.

Можно заметить, что амплитуда сигнала на зонде, полученная методом FIT, меньше по сравнению с теоретическими расчетами. Судя по всему, краевые токи на границе компенсируют/уменьшают вторичные импульсы.

Заключение

В работе представлено новое аналитическое выражение во временной области (11) для диаграммы направленности элементарного излучателя плоской апертуры антенны в зависимости от времени и угла интегрирования. Также получено новое выражение (13) для первообразной импульсной характеристики круглой апертуры в виде эллиптического интеграла второго рода. Последнее выражение может быть применено к плоской апертуре любой формы. Форма плоской апертуры в (13) определялась только сегментом интегрирования или в некоторых случаях несколькими сегментами.

Полученные выражения для поля позволяют более точно рассчитать поле больших плоских металлических апертур, где численные методы вычисления (FIT, метод моментов и т. д.) становятся труднореализуемыми с точки зрения временных и вычислительных затрат. Таким образом, с помощью аналитического метода, основанного на физической оптике и апертурной теории во временной области, повышается точность метода для линейно поляризованного поля.

Предложенный метод позволяет проще и с большей точностью решить задачи, связанные с пространственным распределением линейно поляризованного поля апертурных антенн.

Публикация подготовлена в ходе/в результате тенн».) в рамках Программы «Научный фонд Нацио-проведения исследования/работы (№ проекта 22-00- нального исследовательского университета «Высшая 035 «Особенности импульсных полей апертурных ан- школа экономики» (НИУ ВШЭ)».