Линейные поперечные колебания вязкой магнитоупругой пластины

DOI:

It is known that the system of multidimensional equations for magneto-elastic solids with weak conductivity was studied in detail in works [1-4]. In these papers, certain equations were derived for the critical values of the magnetic field in the presence of an oscillating frequency. The magneto-elastic formulas of magneto-elastic plasticity generate threedimensional equations even after implementation through Kirchhoff's hypothesis. Two-dimensional magnetoelasticity equations for a finite-dimensional magnetoelastic ferromagnetic thin plate are derived. The main quantities and oscillation amplitudes characterizing the internal and external induced magnetic field of the thin plate are interconnected through the equations of motion and boundary conditions.

The above-mentioned relationship makes it difficult to sufficiently indicate the phenomena occurring in the transverse oscillations of magneto-elastic plastics of a certain size [4,5]. In this article, the problems aimed at the solution of transverse vibrations propagating in a thin magneto-elastic plate located in a magnetic field are posed, and a scientific methodology for their simple solution is developed. It is possible to obtain a general solution to the problem, independent of the dimensions, shape, and intermediate boundary conditions of the magnetic plate. We assume that the wave properties occurring in thin plates obey the laws of classical theory, as is known to us. The main results obtained on the basis of the equations below can be applied to plates of infinite size. Taking into account that the magnetic susceptibility and magnetic receptivity of the material under study are sufficiently large and the thickness of the plate is very thin, a theoretical methodology is proposed, which allows deriving an integrodifferential equation for the amplitude of transverse oscillations of a magnetoelastic plate.

Provided that the magnetic susceptibility is very large compared to unity, magnetostatics problems can be solved in both internal and external fields. When using the Galerkin method, the determination of frequencies is reduced to solving a system of infinite algebraic equations

PROBLEM STATEMENT AND SOLUTION

METHOD

The differential equation of motion of a body in an electromagnetic field satisfies Maxwell's equation and can be written in vector form as

divD = pe,

divB = 0, dB

rotE = - ~t,            (1)

rotH=/ + g.

The first equation in this system of equations represents Gauss's law, the second equation represents the absence of a magnetic field, the third equation represents Faraday's law, and the fourth equation represents Ampere's law. In most cases, the expression div/ + ^- =0 is added to this system of equations. This is considered a continuity equation dN   г (    м dN d2N\

— = FAa, t.N,—,—), да       \        dt dt2 J

Boundary conditions in this

gN(ao,t) = b1, g2N(aN,t) = b (3)

and initial conditions t = 0: N = 0,  — = 0

d t

where N = [u, w, 9 a , N a , Q a , ^M a , E p , B y } ,F i is a vector function, generally a non-linear function; 9 i , 9 2 - rectangular matrix; b_lf b₂ - vector quantities.

A plate located in the Cartesian coordinate system (x, y, z) (in the (x, y) plane) is subjected to an external magnetic field B₀(0, B₀,0) (B₀ = const).

The plate is made of a soft ferromagnetic material. Fig. 1 shows the transverse dimensions of the ferromagnetic plate sample, which have values 2a, 2h and 2b.

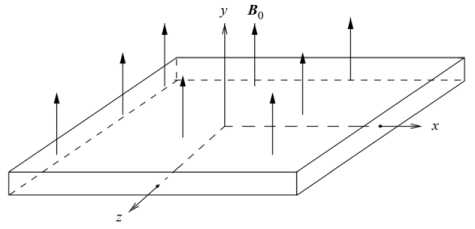
Fig. 1. Schematic diagram of a sample of a ferromagnetic thin plate.

A ferromagnetic plate is placed on an external magnetic field, in which the direction of the lines of force induced by the magnetic field is shown in Figure 1. We assume that the forces produced by the magnetic field are the forces acting on the plate. The conductivity properties of the plate are directed along the flow and are very small compared to the forces generated and are not taken into account. The considered ferromagnetic plate depends on the magnitudes characterizing the external magnetic field and the magnetization vector of the plate material and its level. In studying the characteristics of deformable solids in the magnetic field, different ways and approaches have been used by researchers, and the solutions of this process have been presented in different ways [8,9]. The viscosity of the plate material is the restoring force

Р е - ^-С_еАе - ^-c e [1 ^- Г е ^(ы к ) ^- iГ е (^ s )]^e,                           ⁽⁵⁾

where

∞

Гут^ ^- I ^R^m⁽P) • cos ы TdT; Г^

∞

(ы)- I 0

Р ^.ц (^т) sin ы zdz.

F_e - repulsive force when the plate vibrates, Ae -deformation; c_e - instantaneous modulus of elasticity [10-12]. A force acting on a body of arbitrary size is proportional to the torque

F u - f_v(Mgrad)B_odv, (6)

^m - ^(r * (Mgrad)B₀ + M к B 0 )dv.  (7)

The differential equation of the drive of a ferromagnetic plate B 0 (0.0.B 0 ) has the following form:

D o V²w + 2ph д^ + _XBo & V²Wdy - Do £ V²w(z)R_d(t - z)dz - 0.

where w(x.y.t) - a value characterizing the elasticity of a plate,

Do - 2Eh3/3(1 - v2). V2- d2/dx2 + d2/dz2

Laplace operator,

Ψ ( x,y,z ) - is the induced potential of the magnetic field inside the plate, which is found as follows:

We can write the above equation (1) in the following form:

ℎ z > ee)               ee) Je)e)

H x 0 = J yy 0^h ,   H y 0 = H z 0 = 0 , ^|z| - ₂ •

H x 0 =- J y 0 z , H y 0 = H z 0 = 0

z-- h:(10)

H ^{( e} ) — 1 T h  H)^e ) — e^e ) — 0

H x 0 = J yi h 0^h ,   H y 0 = H z 0 = 0 .

The corresponding voltage components are proportional to the electric field strength if |z| — h, then

E_x 0 = 0,   E y 0 = J y ₀ / a ,   E z ₀ = 0   (11)

if | z | > ^ then E^ -E^-E^-0.

If we take into account the boundary conditions at the surface of the plate, then z - ± ^ , when B ;± _o -

± —]уч is present.

,                  dw0(q)

72Ф1(р)-0,ре^, dWi(q) dn

- d(q) +

dФ o (q) dn

.qeS;

Р²Ф_к(р) - 0.p e R₃\Q i ,

ФкЫ - f(q) - W k (q). qeS;(k- 1.2....)

^(p) = 0,p e 01, dVkW _ дФк-1(д) dn        dn

,qeS; (k = 2,3....).

In this case, the positive direction (corresponding to the positive direction of the axis) produces a negative value of the deflection. If there is an external current moving in a negative direction, the motion of the ponderomotive forces associated with it coincides with the direction of action of the normal component of the mechanical load. From Fig. 2 it can be seen that with an increase in the values in the negative direction, the deflection value increases in absolute value.

When the external current flows in a positive direction, part of the Lorentz force that appears on the plate under the influence of the external current is directed opposite to the direction of action of the remaining forces. The deflection decreases with the current value. With a further increase in the current density, the deflection becomes positive. At the same time, at the initial moment of time, the deflection becomes negative. This is because at the initial moment of time, the external current has a smaller effect on the deflection than the effect of other forces applied to the plate.

For this system of equations (13), the following boundary conditions hold: r ^ м when Ф_к ^ 0, and r ^0 when | W k | < M [13,14].

From the system of equations (13) given above, it follows that W o = const. By choosing arbitrary constants for the functions, W_o = 0. In this case, Ф 0 is a solution to the Dirichle problem.

Wo(r,o) = 0, да

*т(г,е) = У (-1)m(fk-R^t-)kcoskO,m = 1,2 k К k=0

Фо(г,0) = 0,

It is necessary to asymptotically estimate the oscillation frequencies of the shells and determine the most active resonance regions of the shells. The oscillations with magnetic induction vector

3(31,0,0)  are investigated. The equations of oscillations have the following form.

D -AAW -

1 d2X h(p - 1)

R dx^ + 4 ■ я ■ д2

132^

■ 32 ■ ^^ - p ■ h ■ 02 ■ W = 0, dx2

For а magnetic field, k₀ - is the relative wave number,

0_r - is the relative frequency.

0 =

N 11 . IN , I ’

W 11

^h См—l) _ -2 4^u^{2   1}

The dimensionless natural frequencies of magnetoelastic oscillations have the following form.

Shells with parameters ^ =4^10 ³, ^ = 2 were made of aluminum.

Щ² = ( _Ж 2 ₊ ^ 2 ) 2

a 4

^{- 2} ■ ⁰ ■ ^a 1 + ₍ -2  --J^

( a 2 + a 2 )²

Numerical results are obtained in Matlab software and their results are shown in Figures 2 and 3.

Theoretical studies of the influence of magnetic field on oscillation frequencies were conducted.

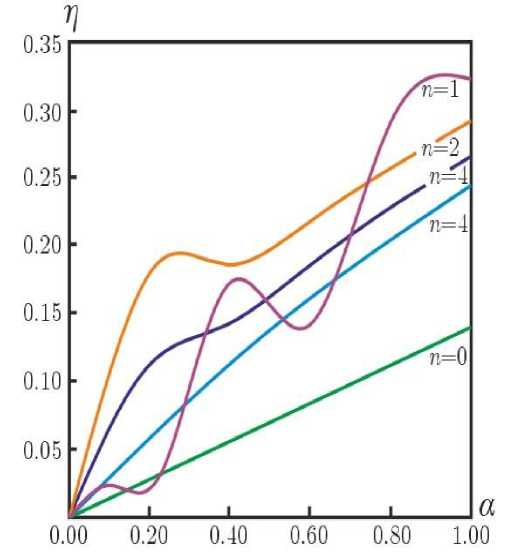
Figure 2. Variation of the plate decrement damping coefficient with the viscosity parameter:

/0 = 5- 10³;^Q 5 • 10⁴;^Q 5 • 10⁵;^Q 5 • 10⁶₂ А / м ².

Thus, a methodology and algorithm for studying the issue of plate vibrations located in a magnetic field was created.

The longitudinal magnetic field has the effect of compressive forces along the circumference of the shell.

The presence of a longitudinal magnetic field reduces the frequency value for higher vibrational forms, "coupling" of frequencies occurs.

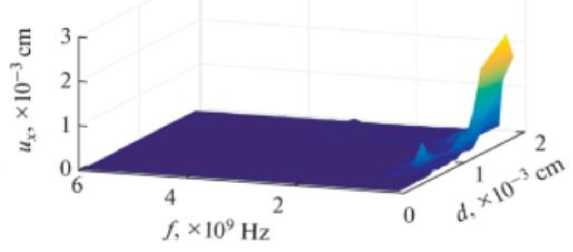
Figure 3. Dependence of the oscillation shape on the frequency.

The presence of an external longitudinal magnetic field lowers the value of the frequency for high vibration areas, where the "adding" of frequencies takes place.

The longitudinal magnetic field exerts effective compressive forces along the shell.

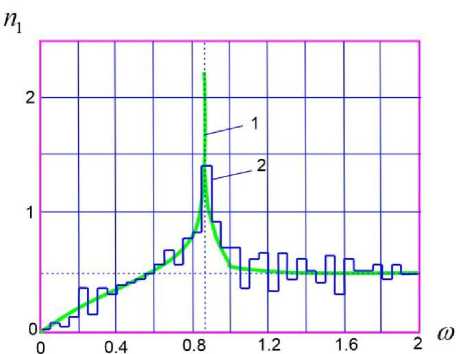
Figure 4. Asymptotic and empirical frequency densities with parameters - = 4-10 ³, - = 2 in p = 0,5 magnetic

R                 '

field.

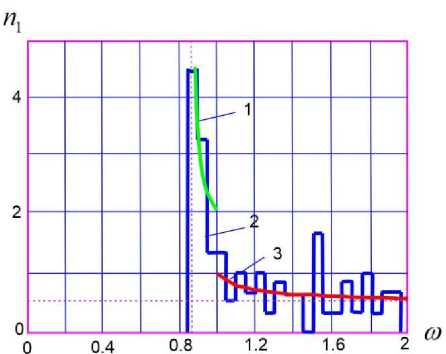
Figure 5. Asymptotic and empirical frequency density with parameters ^- = 4-10 ³, aj = a₂ = R in p = 0,5

R

magnetic field .

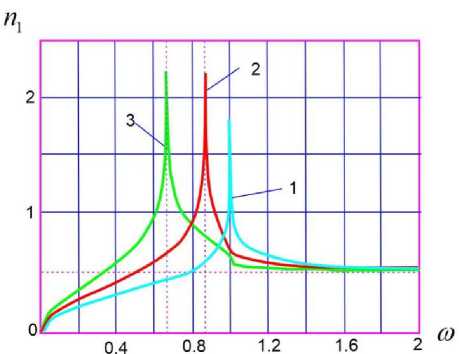
Figure 6. Asymptotic frequency density with parameters H = 4-10 ³, A 1 = A 2 = R in the following magnetic field

(curve I - в = 0 , curve II - в = 0,5 , curve III - в = 0,75).

An asymptotic formula for frequency density is determined.

n(Q)

пс

Here

' 2

я

= ’ я

2 Iя

ш

■^11-

■ р^

ш + /1

—

-2

■ К(к), ш >1

■[2- К(к) - Р(к,ф1)],

тМ^-М

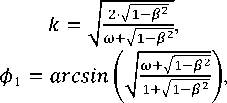
Т1 —-2 < ш < 1

0 < ш < Т1--2

Ф 2

^-T2 = arcsin -----.

1 + ТТ—-2

At zero magnetic field, the cylindrical shell has an asymptotic point of frequencies that correspond to

ti2=-R2

Р

As can be seen in Fig. 6 curve II and III, we can observe that the asymptotic point of condensation ш * = Т1 — -² shifts to the low frequency region. In this case, a longitudinal compressive effect occurs on the shell. When designing electrical equipment operating under the influence of a magnetic field, the shell exhibits a very active resonant state. The frequency density of the shell tends to the Courant density, where its value has a constant value of ω ˃ 1.

CONCLUSION

To compare the asymptotic estimates, studies and calculations were carried out using numerical modeling methods. Natural frequencies are asymptotic estimates for the frequency density, reflecting the nature of the distribution. Using V.V. Bolotin's asymptotic method, it is possible to obtain a solution to the dynamic edge effect in an arbitrary combination of transverse and longitudinal magnetic fields for the conditions of fixing the ends of rectangular plates.