Линейный анализ динамики малых возмущений в модели Грина-Нагди
Автор: Шантыр Антон Леонидович
Рубрика: Естественные науки: новые проблемы и инновации
Статья в выпуске: 11, 2013 года.
Бесплатный доступ
Уравнения мелкой воды, система грина-нагди, дисперсионное уравнение, свободная поверхность, неоднородность, линейный анализ, волновой вектор, собственная частота
Короткий адрес: https://sciup.org/14967891
IDR: 14967891
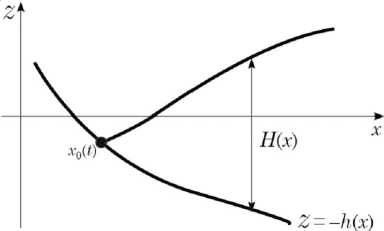
Список литературы Линейный анализ динамики малых возмущений в модели Грина-Нагди
- Баутин, С. П. Исследование начально-краевой задачи для системы уравнений Грина. -Нагди/С. П. Баутин//Вестник Уральского государственного университета путей сообщения. -2012. -№1 (13). -13 c.
- Воронин, А. А. Задача управления гидрологическим режимом в эколого-экономической системе «Волжская ГЭС -Волго-Ахтубинская пойма». Ч. 2. Синтез системы управления/А. А. Воронин//Проблемы управления. -2012. -№ 6. -С. 19-25.
- Ландау, Л. Д. Гидродинамика/Л. Д. Ландау. -М.: Наука, 1986. -736 с.
- Храпов, С. С. Численная схема для моделирования динамики поверхностных вод на основе комбинированного SPH-TVD-подхода/С. С. Храпов//Вычислительные методы и программирование. -2011. -№ 1. -Т. 12. -С. 282-297.
- Храпов, С. С. Моделирование динамики поверхностных вод: монография/С. С. Храпов. -Волгоград: Изд-во ВолГУ, 2010. -132 с.
- Khrapov, S. The Numerical Simulation of Shallow Water: Estimation of the Roughness Coefficient on the Flood Stage/S. Khrapov//Advances in Mechanical Engineering. -2013. Vol. 2013. -Article ID 787016. -11 p.
Краткое сообщение
