Liquid crystaloptical shutter for stained glass and windows

Original article

A t present, the variety of materials used in production, industry, and technology cannot be overestimated.

Scientists and engineers work on the creation of new materials that can expand the technical capabilities and allow the creation of fundamentally new devices that can be used in various branches of human activity [1–26]. These materials include nanomaterials. As you know, nanomaterials are materials that have been created on the basis of nanoparticles or using nanotechnologies. Their characteristic sizes range from 1 to 100 nanometers. Tubes, fibers, clusters, tapes, dispersions, films are known with the nano prefix, and this series can be continued.

A separate huge layer of problems is solved using carbon materials (fullerenes, graphenes, tubes, diamonds, fibers). The development and search for new nanomaterials has been going on for decades, which opens up prospects for the development of technologies. The nanomaterials mentioned above have a crystalline structure.

In construction, as well as in decor, liquid glass is widely used, for example. This is a very dense and viscous substance at a working temperature of 95–98оC, after being applied to the surface, it hardens. It is used for waterproofing, such as foundation, has good adhesive characteristics, the material is thermal resistant, moisture resistant, non-toxic, fireproof, has antistatic and antiseptic properties, the treated surface has a long service life.

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS

The disadvantages include the possibility of getting burns upon contact with the skin due to the presence of alkali in the composition; dries quickly, so you need to have the skill to work with it; effectively applied to concrete and wood, but destroys the structure of the brick.

One of the materials, which is referred to as nanomaterials due to the small size of molecules (from 5 to 30 Å), has found application in science, technology, and in the development of various engineering solutions, is a liquid crystal (LC). A liquid crystal has the properties of both a solid and a liquid. It is viscous and fluid like a liquid, but at the same time it has a strict orientational order of molecules like a solid body. These are organic substances that are contained in a living organism (for example, cholesterol), and therefore liquid crystals are successfully used in medicine to create devices and methods for the early diagnosis of diseases; thin LC films are considered as models of cell membranes [19]. Liquid crystals are used in technology to create monitors, scoreboards, various gauges, sensors, both for information display systems and as a “working substance” for controlling pressure, vibrations, levels of liquid or bulk substances [1–24].

The unique physical properties of liquid crystals make them sensitive to external influences. So, when heated, connected to electric or magnetic fields, various kinds of mechanical actions (shift, bending, torsion), liquid crystals demonstrate many different effects, on the principles of which the operation of already created devices is based, and the prospects for their use are endless.

Liquid crystals show very unusual and beautiful pictures that can be used for decoration and interior design (Fig. 1, photos taken from open sources).

The author of the article had experience of creative cooperation with the Design Department of the Ufa State University of Economics and Service. Photos obtained during the physical experiment with liquid crystals were used in interior design. As a result of such joint work, exhibitions were held in Ufa in the art gallery “Academia” “Creativity of liquid crystals”, as well as in the National Center for Contemporary Art in Moscow “Physical picture of the world: visual images of liquid crystals”.

Designers and architects are constantly looking for new solutions in architecture and color. One can draw ideas, in particular, by studying the structure of matter,

Fig. 1. Textures in liquid crystals observed under a microscope

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS armed with a microscope (Fig. 2, photographs taken from open sources).

Liquid crystals have anisotropy of physical properties, i.e. they manifest themselves differently when exposed to the crystal in different directions. The anisotropy of properties is also due to the structure of LC molecules. The shape of a liquid crystal molecule can be approximated as a banana, disk, or stick [25, 26]. We will consider liquid crystals with elongated molecules with a diameter of about 5 Å and a length of about 30 Å.

Due to the anisotropy of physical properties and the shape of molecules, liquid crystals exhibit a variety of different effects that are not observed in liquids or solid crystals. In solids, the effect of birefringence is observed

Fig. 2. Futuristic architecture and colors

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS during mechanical deformation of an I-beam. If we take a thin layer of liquid crystal placed between glasses, look into the microscope eyepiece, the polaroids of which are crossed, then we will see a dark field. When the crystal is exposed to an external field, it is possible to ensure that the crystal layer will transmit a light beam. That is, under certain conditions, a cell with a liquid crystal either transmits light or not, so it can be used as an optical shutter.

In solid crystals, the piezoelectric effect is known [25, 26], which consists in the appearance of an electric field during mechanical deformation. A similar effect takes place in a liquid crystal, it is observed when, for example, shear deformations occur, and is called the flexoelec-tric effect (“flexo” – bending). As a result of bending deformations, surface polarization appears in the liquid crystal; in addition, the wedge-shaped or crescent-shaped form of LC molecules leads to the appearance of a local deformation of the director field и (director is a vector characterizing the predominant direction of orientation of LC molecules).

If the crystal molecules are oriented in a horizontal plane, then this orientation is called planar; if the molecules are oriented vertically, then this orientation is called homeotropic.

This article presents the results of an experimental study of the effect observed in liquid crystals, thin layers of which can serve as an optical shutter (curtain or blinds) for stained glass or windows of buildings and structures.

MATERIALS AND METHODS

Materials

For the experimental study of the flexoelectric effect, nematic-type liquid crystals (NLC) were used, the main parameters of which are given in Table 1.

Methods

Samples with a homeotropic orientation of molecules with a thickness h from 10 to 100 µm were studied by the method of birefringence. The shear frequency is about 1 kHz.

The cell with a liquid crystal was made of two glass plates in the form of a flat capacitor (Fig. 3), spacers were placed between the glasses, which set the sample thickness. The substrates were coated with a conductive coating of metallic chromium, which made it possible to obtain the required orientation of LC molecules. To maintain the required temperature for the existence of the mesophase, the cell was heated, the temperature was controlled by a thermocouple.

The samples were placed on the object stage of an optical microscope. The light beam passed through the experimental cell, and its variable component was recorded by a spectrophotometric attachment. A DC millivoltmeter was used to record the constant component of the optical signal. A source of shear vibrations was located on the side of the microscope stage, which was connected to the LC cell using a thin waveguide. The technique of experimental studies is described in detail in works [6, 8].

RESULTS AND DISCUSSION

We will study the flexoelectric response of the LC system to a shear-type perturbation, in which one of the bounding surfaces of the layer performs periodic oscillations at a speed of 15 . We will also consider LC layers only with a uniform orientation of molecules.

According to the geometry of the problem, the director is headed vertically parallel to the Z axis, the velocity vector of the plate vibrations is horizontal along the X axis. The orientation of the liquid crystal molecules in

Table 1

Physical parameters of liquid crystals

Liquid crystal	Mesophase temperature, оC	е 11 , 10–4 units CGS/сm	е 33 , 10–5 units CGS/сm	Dipole moment, p , D	Dielectric anisotropy, ε α
cyanophenyl ester of heptylbenzoic acid (CPEHBA)	45o   56o K — N — I	5.5	3	~4,5	~19
nitrophenyloctyloxybenzoate (NPOOB)	oo K4—5 А —61 I 68o — I	5.0	1	~4,1	> 0
n- methoxybenzylidene-n-butylaniline (МBBА)	18o   42o K — N — I	4.5	102	~2,6	< 0
butylheptanoyl azoxybenzene (BHAXB)	20o   71o K — N — I	4.0	30	~3	> 0

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS

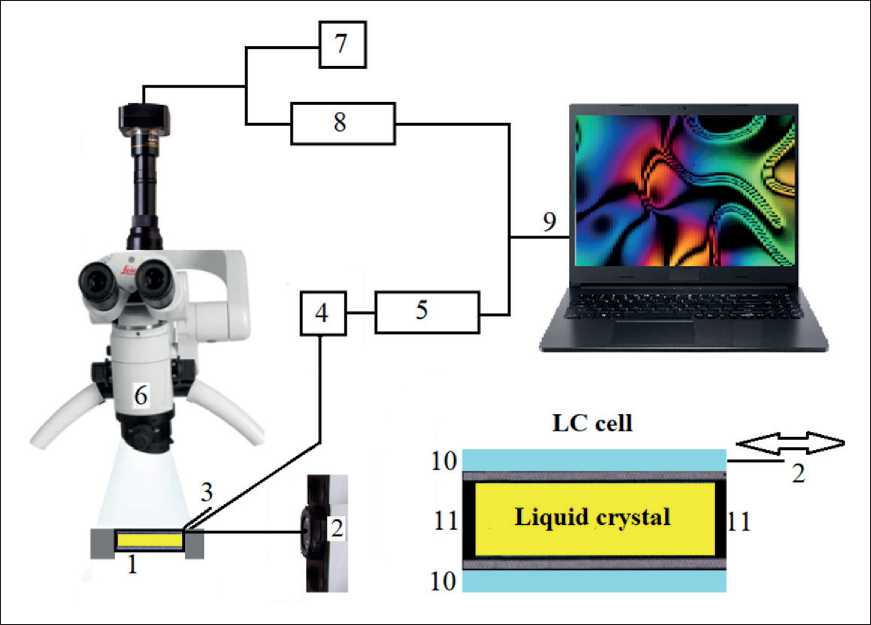
Fig. 3. Elementary setup for experimental detection of the flexoelectric effect in LC:

1 – condenser cell with LCD; 2 – vibration source (shift); 3 – thermocouple;

4 – dc millivoltmeter; 5 – analog to digital converter; 6 – microscope; 7 – dc voltmeter;

8 – selective amplifier; 9 – computer; 10 – motherglass; 11 – gaskets

the volume is characterized by the angle θ . The equation describing the distribution of the angle θ along the Z axis can be written in general form [26]:

pi)o

6 =--- exp 4iQ

V2

—— b(z -5)

cos

V2

— b(z -<5)

coscot. (1)

Here η ₁, η ₄ are viscosity coefficients; δ is the distance at which the director has a deviation from the initial orientation; the real part of the roots of the characteristic equation: b ~[( η ₄ ρω ²)/( η ₃ K ₃₃)]^1/2; K ₃₃ – coefficient of elasticity; ω is the frequency of the periodic shift.

According to equation (1), an elastic-viscous wave propagates between the moving and stationary substrates of the LC cell, which leads to a perturbation of the initial homeotropic orientation of the director field (Fig. 4b). Moreover, the director distortion profile in the plane formed by the velocity vector and the wave vector Q is a B-type deformation (bend), which means that in the volume of a nematic liquid crystal, only B-type flexoelec-tric polarization can also be induced, the vector of which lies in the plane of the LC layer. This directly implies that the potential difference between the plates of the capacitor cell must be equal to zero, since the polarization projection onto the normal to the layer is equal to zero. How- ever, in reality, between the conducting substrates, when the initial orientation is perturbed by a shear, an EMF variable is recorded, in which both the first and second harmonics U1ω and U2ω can be distinguished (Fig. 4 a, c).

Consider the dependence of the first harmonic U_1ω on the shear rate (Fig. 4 a, ω =1 kHz), for example, in NLC MBBA at a given temperature Т = 25^оС. In this dependence, along the abscissa axis, we distinguish two areas characteristic of the behavior of U _{1 ω} : 0 <  υ <  υ _c and υ >  υ _c, where υ _c are the values of the speed at which there is a jump in the value of U_1ω and a change in the tangent of the slope angle U_1ω relative to axes υ . In the first region, the first harmonic weakly depends on the magnitude of the velocity or, which is the same, on the displacement amplitude a . When υ ≈ υ _c experiences a jump. Polarization-optical studies have shown that in this case, a stationary tilt of NLC molecules θ _с is induced in the layer, which, apparently, leads to a sharp increase in the harmonic value.

Without specifying the details, we point out that the reasons for the appearance of a stationary distribution of the director angle θ _с in such a geometry can be various, for example, due to the nonlinearity of the equations describing the behavior of liquid crystals with respect to

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS аb

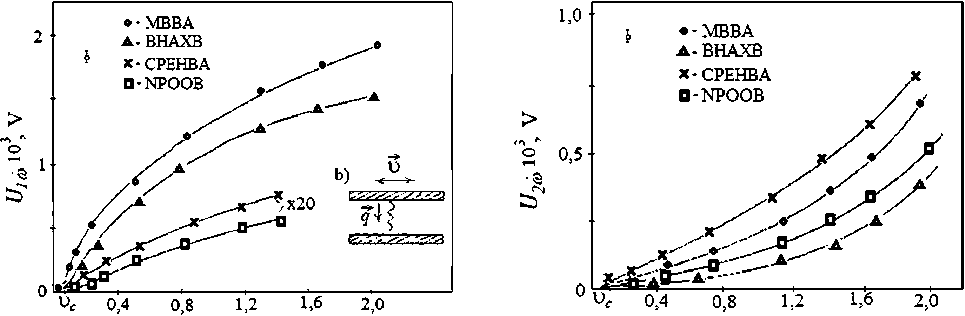
U, cm's                                                             V, cm's

Fig. 4. Dependence of the first harmonic U _1ω on the oscillation rate: a) illustration of orientational distortion in the LC volume under the action of a periodic shift; b) dependence of the second harmonic U_2ω on the oscillation rate (temperature of existence of the nematic phase T_N LC: 25^оС (МBBА), 25^оС (BHAXB), 48^оС (CPEHBA), 3^оС (NPOOB)

the velocity of movement [25] or due to the nonstrict linear motion of the movable plate in one plane, which becomes elliptical [26]. In this case, we will rely on the experimental fact of the presence of such a distribution and show that, in this case, a polarization component appears that is perpendicular to the LC layer.

Let us consider the case when the direction of the X axis coincides with the direction of oscillation of the plate, and the Z axis is perpendicular to the NLC layer. Then we can use equation (2), and the polarization along the Z axis at a small inclination of the director n to the axis will be expressed:

oz where θd – amplitude of director oscillations. It follows from this expression that at a non-zero value of the stationary tilt angle of the liquid crystal molecules θс, a variable potential difference arises between the conducting substrates, which is associated with the flexoelectric effect. To determine the slope θс in the layer, we studied acousto-optic effects, i.e., modulation of polarized light by orientation perturbations in a cell with an LC (Fig. 5).

The relative value of the second harmonic I_2ω / I_o oscillates depending on the absolute value of the speed. From which we conclude that a constant tilt of the director relative to the Z axis is induced in the cell, since intensity minima correspond to the phase difference between ordinary and extraordinary light waves, equal to ∆ = πn ( n = 1,2,3,…). We find the dependence of the angle of inclination on the speed of oscillation of the movable p l ate (Fig. 5). Knowing the value of the average a n gle в_c and the amplitude of the director deviation и 0_d , it is possible to determine the values of the

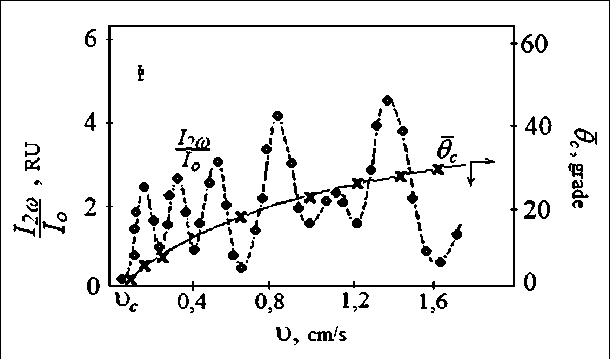
Fig. 5. Dependences (о) – the degree of modulation of the intensity of the transmitted polarized light through the cell with LC MBBA; (×) – shear-induced tilt angle 6_c on shear rate υ

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS flexocoefficients е33 of the studied substances, because the measured value of the first harmonic depends on the listed parameters as follows:

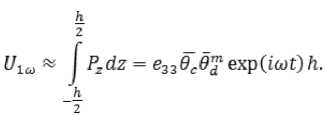
Exp r ession (3 ) is t r ue under the condition that t h e angles 9 _c and 9 d , 9c > 9_d are small, and also if | θ_c ( z )– 9 c | << 1, i.e. the sta t ionary deviation θ_c ( z ) slightly differs from the average 9_c [26], θ_d^max is the maximum amplitude of the director osc i llation in the layer, which is related to the average value 9_d , measured in the experiment by the li ght flu x modulation amplitude. Based on formula (1), о_d^m and 9 are related as follows: dd

9d^j 6ddz = e^W1, where λ = | Q| – damping decrement of elastic-viscous wave.

Then expression (3) will be written as:

Ui^ ^ e₃₃6_c6_ci(Ah²)exp(iut) .

The presence of a sufficiently large value of flexo-modules makes LC promising in terms of the possibility of recording acoustic vibrations and the development of acoustic transducers. But for this, in addition to the existence of a direct flexoelectric effect, it is necessary to know the amplitude-frequency characteristic of the signals generated due to shear disturbances created by oscillations of one of the substrates.

Studies have shown that the frequency response of the signal U_1ω (Fig. 6) (shear rate V = const), for example, in MBBA is similar to the dependence U_1ω ( ω ), obtained with bending-type perturbations. This means that cells of this type can actually be used as detectors of acoustic vibrations in the low-frequency region from 20 to 1500÷2000 Hz, although there is evidence of the use of similar structures for recording sound fields using a light beam – a probe up to frequencies of ω~ 10÷15 kHz.

Let us now turn to the consideration of the second harmonic. As shown above, the appearance of the second harmonic is associated with the orientational modulation of the polarized surface layer – surface polarization by an elastic-viscous wave, which leads to a periodic change in the capacitance of this layer, which manifests itself in the form of generation of surface charges at a double perturbation frequency. That is, the appearance of the second harmonic is a threshold one, and the threshold value of the rate υ_с ~8 mm/s of the appearance of U_2ω ( ω ) coincides with the appearance of a stationary tilt of molecules in the layer. However, there are differences in the ratio of signals U_1ω and U_2ω . With a shift U_1ω >  U_2ω , which means that е ₃₃ >  е ₁₁, for example, in MBBA and BHAXB.

An experimental study of the mechanisms of molecular-orientation polarization of liquid crystals excited by acoustic perturbation showed that in uniaxial crystals, which are the majority of nematics, there are two flexo-electric coefficients е ₁₁ and е ₃₃. Moreover, both dipoles and quadrupoles contribute to the total value of the coefficient е ₁₁, although in different “weight” ratios. This conclusion is the result of the analysis of temperature dependences of the first EMF harmonic U_1ω and acousto-optical effects. However, the question of the “weight contributions” of the listed mechanisms to the flexocoefficient е ₃₃ remains open. In this regard, it is necessary to study the temperature dependences of the е ₃₃ flexomodule. To do this, we study the temperature behavior of the EMF induced at the

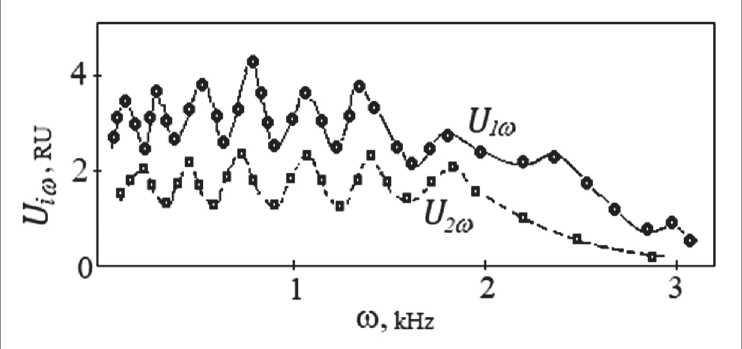
Fig. 6. Frequency dependences of U _{1 ω} and U _{2 ω} harmonics for MBBA ( T _N = 25^оС)

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS

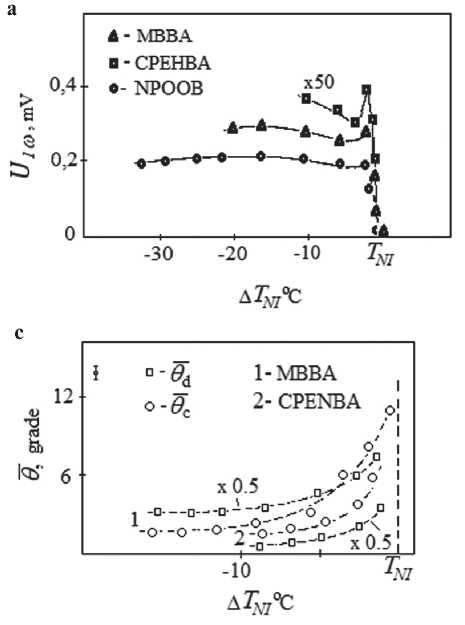
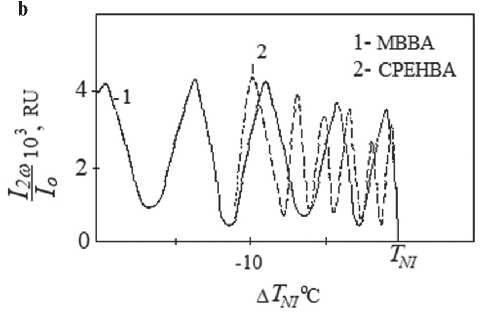
Fig. 7. Temperature dependences:

a) of the first harmonic U_1ω

( а = const, ω = 1 kHz);

b) acousto-optic effect I_2ω/I_o ;

c) deviation angle О_d and angle of constant inclination in the cell with LC о

c

frequency of the first harmonic, as well as the temperature dependences of the constant tilt angle of the director θ _c , induced by shear oscillations of one of the substrates, and the amplitude of the director oscillation 9 d .

Consider the temperature dependence of U _{1 ω} , for example, in NLC MBBA (Fig. 7 a). Far from the phase transition between a nematic and an isotropic liquid, the signal recorded at the first harmonic behaves quite regularly and is understandable from the point of view of phenomenology, i.e. its value, decreasing, can be a function of the order parameter S , as predicted by the theory of the flexo-electric effect. However, when approaching the phase transition, the regression of the signal U_1ω stops, and then its value increases up to the temperature transition of the nematic – the isotropic state T_NI , which is already inexplicable within the framework of the theory. To understand this behavior, let us turn to formula (4). It follows from it that the value of the signal U_1ω is proportiona l to the flexcoefficient е ₃₃, the average constant tilt angle 9_c in the LC layer, and the amplitude of the director oscillation 9_d , which, like the modulus е ₃₃, can be temp e rature d ependent. Note that in this case, the parameters 9_c an d 9_d w ere experimentally chosen to be small, although 9_c > 9_d . From here, having obtained the dependences 9_c ( Т ) ^c and 9_d ( Т ), we can construct the temperature dependences е ₃₃( Т ).

Previously, it was established that in a cell with an NLC having an initial uniform homeotropic orientation, some constant director slope 9_c is induced by a shift

(Fig. 7). Let us choose such a value of the velocity along the abscissa axis, so that due to the presence of a slope during the passage of the LC layer by polarized light, the phase difference ∆ remains less than π , and let’s see how the second harmonic of the optical signal I_2ω / I_o will depend on temperature (Fig. 7 b).

Attention should be paid to the oscillating nature of the dependence of the relative intensity of the transmitted extraordinary wave I_2ω / I_o . Since the initial phase difference is ∆ <  π , then such behavior c an only be a consequence of an increase in the angle 9_c , because the other parameter, the optical anisotropy ∆ n ( T ) decreases as the phase transition approaches, as a function of the order parameter S .

It is possible to estimate how many times the angle θ_c changes when approaching the transition temperature of the nematic – isotropic sta t e T_NI . Dependence I_2ω / I_o ( T ) has five minima, and since 9_c ²~ πn (where n is the number of minima), then 9_c ~√ n ~2,3 times. In fact, if we take into account the correction for the temperature change in the o ptical anisotropy, we obtain the corrected dependence 9_c ( T ) (Fig. 7 c), the value of the angle increases by a factor of 4.5, which is consistent with the result of [25] for MBBA. In addition, the envelope I_2ω / I_o ( T ) can be used to judge the dependence of the magnitude of director oscillations, since the values of the maxima a re proportional to the squared amplitude of the director 9_d ², which also increases towards the phase transition. To verify this result,

RESULTS OF RESEARCH OF SCIENTISTS AND SPECIALISTS

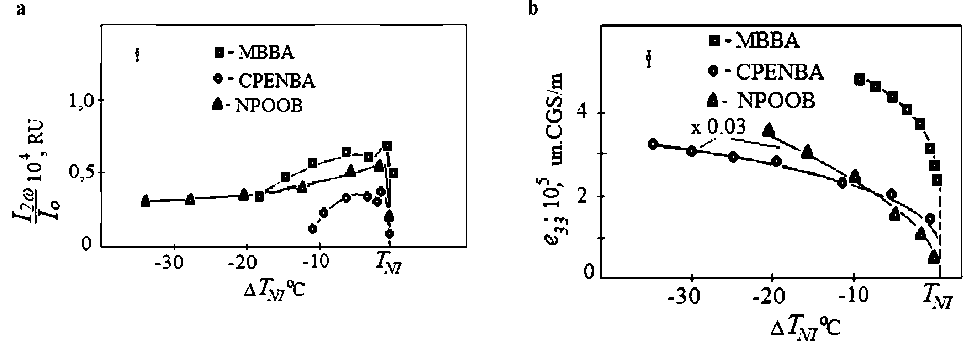
Fig. 8. Temperature dependences of a) acousto-optic effect I_2ω / I_o ( а = const, ω = 1 kHz); b) flexoelectric coefficients е ₃₃ LC (MBBA, NPOOB, CPENBA)

we study the temperature behavior of the value I_2ω / I_o ( T ) under the cond it ion that ∆ <<  π , when the value of the constant slope 9_c ≈ 0, i.e. the director oscillates under the action of a periodic shift around the initial homeo-tropic state (Fig. 8). The value of I_2ω / I_o ( T ), as expected, increases towards the phase transition, which is explained by the growth of 9_d . From here, knowing the temperature changes in the values included in the formula for U_1ω (4), we obtain the dependences of the flexocoefficients е ₃₃ for the substances under study (Fig. 8 b). Let’s discuss these dependencies.

It can be noted that the functional behavior of е ₃₃( Т ) in these LCs, or rather in their nematic phase, is described by the general dependence on the order parameter S as e ~ α S + β S ². All values of the weight coefficients differ significantly for different NLCs, but are consistent with the data obtained for the е ₁₁ modules by the bending vibration method. For MBBA α~0,1, β~0,9; for BHAXB α~0,3, β~0,7; and for CPENBA, NPOOB, OCB α~1,0,

β~0. The values of α and β for MBBA indicate the occurrence of a dipole mechanism of flexoelectric polarization. In the case of CPENBA α~1, and β~0, this means that in this case there is a quadrupole character of flexopo-larization.

CONCLUSION

Thus, the article considers the flexoelectric effect observed in thin layers of nematic liquid crystals with homeotropic orientation of molecules placed between two glass plates. The occurrence of the effect has a threshold character, the critical strain rate is about 8 mm/s. The conditions and parameters of the effect (shear amplitude, sample temperature) on a condenser cell for various liquid crystals are considered. It is proposed to use the results obtained to create an optical shutter (shutter) for stained-glass windows or windows of buildings and structures.