LMI Fuzzy Observer Design for Cryptography in Wireless Mobile Communications
Автор: P.Sivakumar, N.Chitra, M.Rajaram
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 8 vol.5, 2013 года.
Бесплатный доступ
Recently the engineering community began to seek the possibly application of chaos. The fact that the cryptographic community had used discrete pseudo-chaotic systems for a long time to generate cipher keys that leads to the initiation of applying chaos to secure communications. This paper presents a schematic design methodology for a fuzzy observer based secure communication of hyper chaotic systems in cryptographic applications. The transmitter and receiver, which are based on a 3D hyper chaotic oscillator, are synchronized by exploiting the concept on the observer from the control theory. The scalar transmitted signal is designed so that the hyper chaotic carrier masks the encrypted signal, which in turn hides the message signal. To encrypt the message signal, an n-shirt cipher with multiple key algorithms is proposed. In receiver side, the fuzzy observer of chaotic system is designed based on the general Takagi-Sugeno fuzzy model. This approach leads to the design of communication systems with higher security.
LMI, Fuzzy Observer, Takagi-Sugeno Fuzzy Model, Cryptography
Короткий адрес: https://sciup.org/15010455
IDR: 15010455
Текст научной статьи LMI Fuzzy Observer Design for Cryptography in Wireless Mobile Communications
Published Online July 2013 in MECS DOI: 10.5815/ijisa.2013.08.08
Recently, there has been much interest in the use of two synchronized chaotic systems for the purpose of secure communication. A chaotic signal has a spreadspectrum and can hide a small message signal in the spectral domain. However, in the time domain, a chaotic chaotic system can be easily identified by using one of its state variables. The idea of chaotic masking is to directly add the message in a noise-like chaotic signal at the transmitter, while chaotic modulation is by injecting the message into a chaotic system as spreadspectrum transmission. Here a secure communication scheme is proposed, which combines cryptography and the synchronization of hyper chaotic systems. The
Transmitter and Receiver, which are based on hyper chaotic oscillator, are synchronized via a scalar signal by exploiting the concept of the observer from Modern Control Theory. In a more systematic design, using the Takagi-Sugeno (T-S) fuzzy modeling and he control and synchronization of chaotic Systems their stability analysis has been investigated extensively. Much research on controller and observer design for nonlinear systems are carried out based on T-S Fuzzy models. The benefit of using a fuzzy model based design is a straight forward manner to achieve the desired objective by using the parallel distributed compensation concept. Chaotic synchronization and its application to secure communication have been discussed frequently in recent years. The method to design an observer for Hyper chaotic oscillator for the purpose of secure communication has been proposed by G.Grassi and S.Mascolo [1998]. This article helps for better understanding of this kind of applications. The article proposed by A.Tamasevicius, A.Namajunas and A.Cenys [1996] discussed the characteristics of simple 4D chaotic oscillator. They discuss about construction and synchronization of 4D oscillators. The article proposed by Tao Yang, Chai Wah Wu and Leon O.Chua [1997] described the cryptographic technique based on chaotic systems. They discussed about N-shift key cipher technique for cryptography. The article proposed by Xiau-Jun Ma, Zeng-Qi Sun and Yan-Yan He [1998] discussed about analysis and design of Fuzzy observers. They discuss about Takagi-Sugeno Fuzzy models. The article proposed by P.Bergsten, R.Palm and D.Driankov [2002] dealt with observers for Takagi-Sugeno Fuzzy system. They discussed about sliding mode observers for T-S Fuzzy systems and sliding mode observers for Dominant Linear Fuzzy systems. The article proposed by Kuang-Yow Lian, Chian-Song chiu, Tung-Sheng Chiang and Peter Liu [2001] discussed about Fuzzy Observer based design of secure communication of chaotic systems by using Takagi-Sugeno Fuzzy Models and Fuzzy Observers. They discuss about various chaotic systems like
Lorenz’s system, Chuo’s circuit, Henon map and Lozi map.
-
II. Cryptography System
A sender wants to send a message to a receiver. Moreover, this sender wants to send the message securely, he wants to make sure an eavesdropper cannot read the message. A message is a plaintext (sometimes called clear text). The process of disguising a message in such a way as to hide its substance is encryption . An encrypted message is cipher text . The process of turning cipher text back to plaintext is decryption. The art and science of keeping messages secure is cryptography, and cryptographers practice it . Cryptanalysts are practitioners of cryptanalysis, the art and science of breaking cipher text; that is, seeing through the disguise. The branch of mathematics encompassing both cryptography and cryptanalysis is cryptology and its practitioners are cryptologists .
-
III. N-SHIFT Key Cipher Technique
The N-shift key cipher algorithm is shown in equation (1). Here the plaintext is shifted N-Times with key K.
e ( p ( t )) = f .... f f p t , k t ,...., k t = y ( t ) (1)
The Non-Linear function f(x, k) is defined as,
'( x + k ) + 2 h ,
f ( x , k ) = < ( x + k ),
/ x + k ) - 2 h ,
- 2 h < ( x + k ) <- h
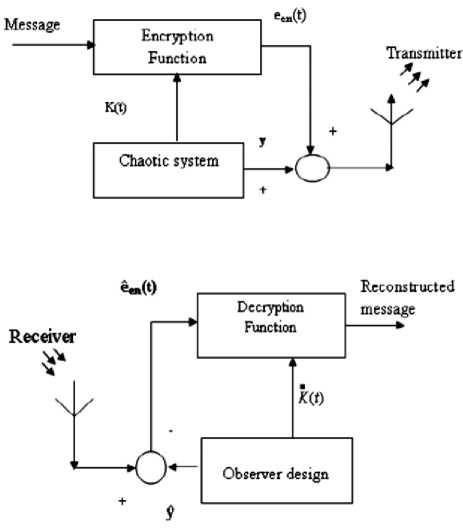
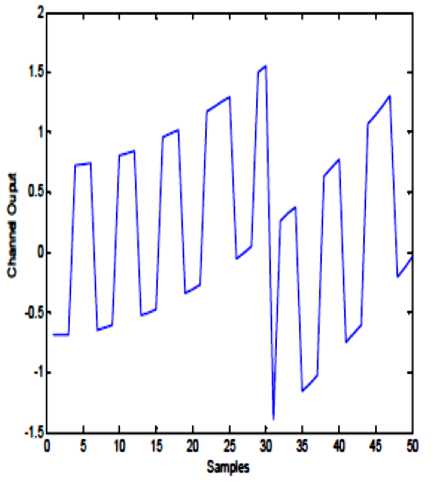
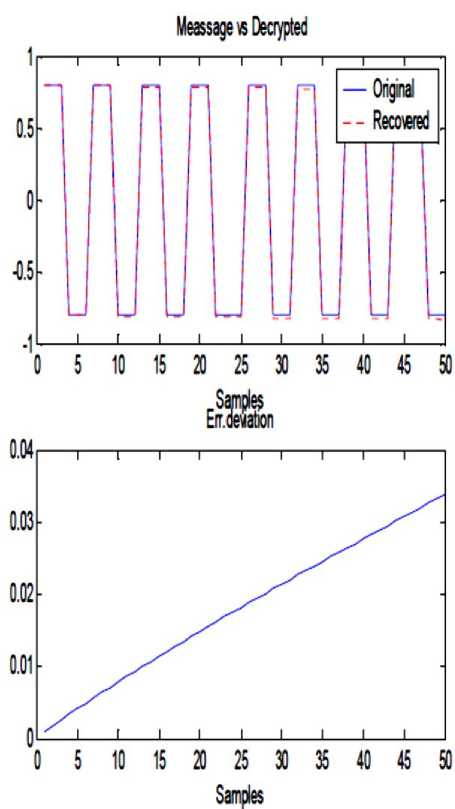
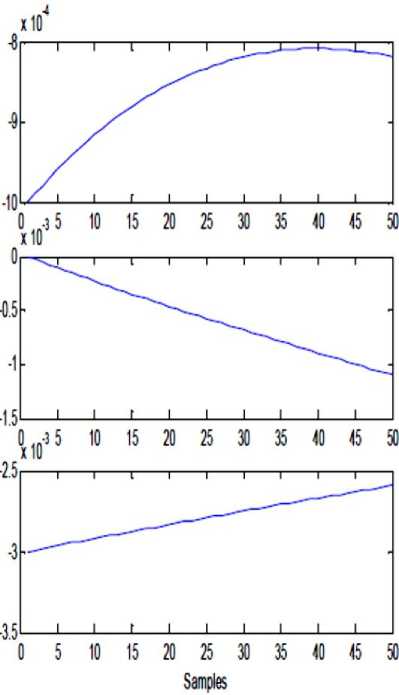
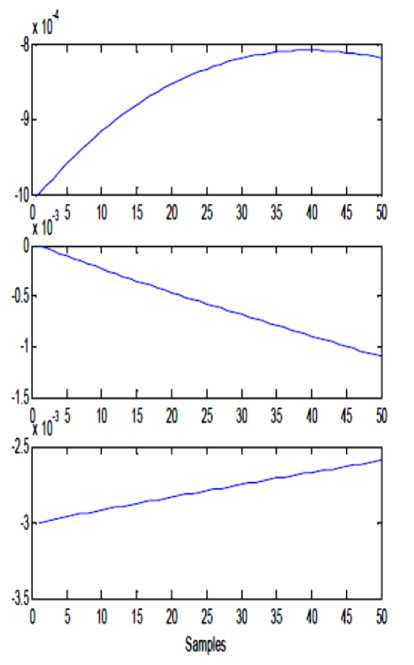
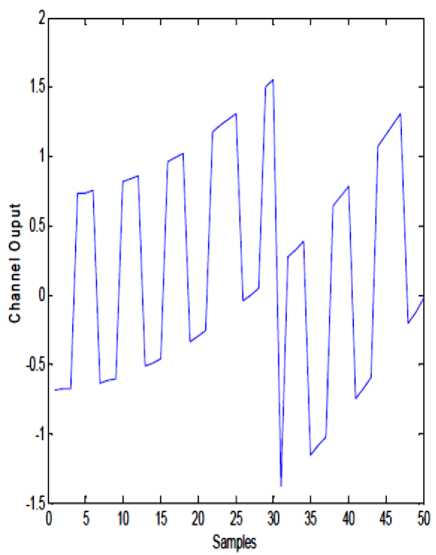
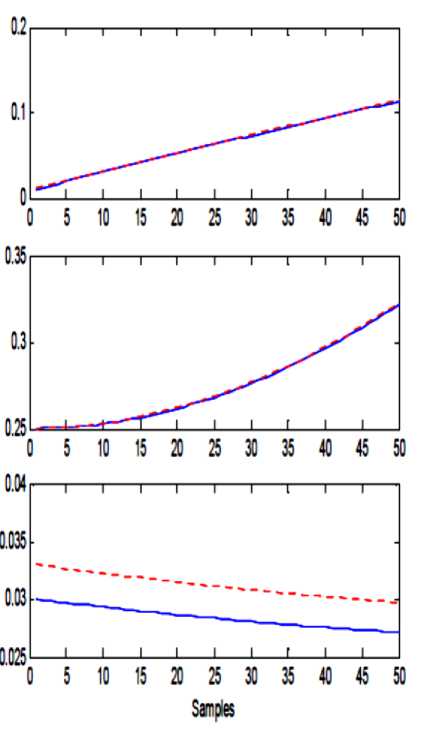
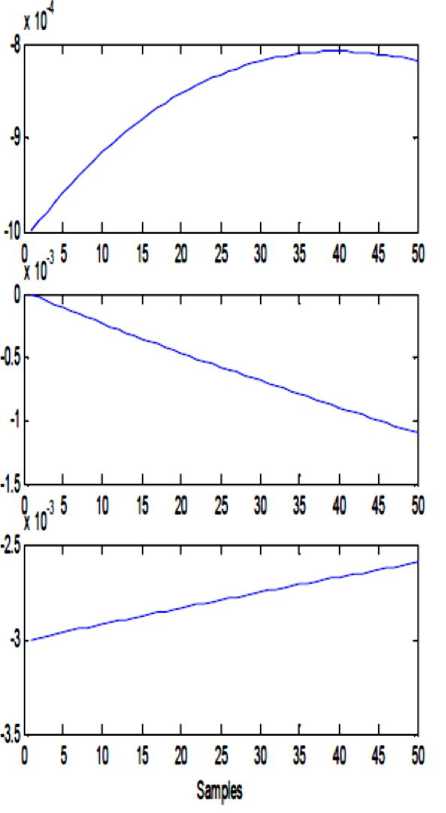
- h ^ (x + k) - h < (x + k) < 2 h Where h is chosen such that P(t) and K(t) lies between (-h, h). This same function is used in Receiver side to decrypt the cipher text to retrieve the original plaintext; the function used in receiver side is, d(een(t)) =f .... f f p t , -k t , , -k t =p(t) (3) Here also the f(x, k) is same as equation. Let A and B be two sets in the universe U Ma (x) and m (x) be the characteristic functions of A and B in the universe of discourse in sets A and B respectively. The Characteristic function Ma (x) is defined as follows: 11, x e A Ma(x) =k „ , 10, x ^ A and Mb (x) is defined as 10, x ^ B The definition of a fuzzy set is given by the characteristic function, Mf : U ^[0,1] In this case the elements of the universe of discourse can belong to the fuzzy set with any value between 0 and 1. This value is called the degree of membership. If an element has a value close to 1, the degree of membership or truth-value is high. The characteristic function of a fuzzy set is called the membership function; it gives the degree of membership for each Element of the universe of discourse. The membership functions for fuzzy sets can have many different shapes, depending on definition some of the possible membership functions, we have: (a) the Г-function: an increasing membership function with straight lines; (b) the L function: a decreasing function with straight lines; (c) Л-function: a triangular function with straight lines; (d) the singleton: a membership function with a membership function value 1 for only one value and the rest is zero. There are many other possible functions such as Trapezoidal, Gaussian, Sigmoidal or even arbitrary. A notation convention for fuzzy sets which is popular in the literature, when the universe of discourse U, is discrete and finite, is given below for a fuzzy set A by A Fuzzy set can be defined as a collection of elements in a universe of information where the boundary of the set contained in the universe is ambiguous, vague and otherwise fuzzy. The theory of fuzzy logic deals with two problems 1) the fuzzy set theory, which deals with the vagueness found in semantics and 2) the fuzzy measure theory, which deals with the ambiguous nature of judgments and evaluations. In fuzzy logic everything is a matter of degrees. . Ma( x1) Ma( x2) A = + ----+... xx =z i Ma(x.-) xi and when the universe of discourse U is continuous and infinite, the fuzzy set A is denoted by Ma(x) x A-f The fuzzification operation, or the fuzzifier unit, represents a mapping from a crisp point x = (x1 x2 … xn) T e X into a fuzzy set A e X, where X is the universe of discourse and T denotes vector or matrix transposition. There are normally two categories of fuzzifiers in use. The first is singleton and the second is non-singleton. A singleton fuzzifier has one point (value) xp as its fuzzy set support, i.e., the following relation governs the membership function: Ma (x) = '1, x = xp e X 0, x * Xp e X The non-singleton fuzzifiers are those in which the support is more than a point. Examples of these fuzzifiers are Triangular, Trapezoidal, Gaussian, etc. In these fuzzifiers, Ma (X) = 1 at x=xp, where xp may be one or more than one point, and then Ma (x) decreases from 1 as x moves away from xp or the “core” region to which xp belongs such that Ma (xp) remains 1. For example, the following relation represents a Gaussian-type fuzzifier: Ma(x) = exP4 Where the variance, CT 2 , is a parameter characterizing the shape of Ma (x) . Defuzzification is the third important element of any fuzzy controller. In this section, only the center of gravity defuzzifier, which is the most common one, is discussed. In this method the weighted average of the membership function or the center of gravity of the area bounded by the membership function curve is computed as the most typical crisp value of the union of all output fuzzy sets: _ J y • Ma ( y) dy c J Ma ( У ) dy Chaotic oscillators are widely used for their inherently broadband and noise like characteristics. These inherent characteristics of chaotic signals are considered as possible highly secure media for communication. In this project work the chaotic masking scheme was used. A chaotic circuit, such as Lorenz circuit, whose state equations are given in equation (9), generates a chaotic carrier, which is used to mask encrypted information the Signal in order to achieve secure communication. Receiver synchronizes the transmitter by using Fuzzy observer and thereby extracts the original message from the chaotic signal, x, (t) = -10 x, (t) +10 x2 (t) x2 (t) = 28 x (t) - x2 (t) - xT (t) x3 (t) 8 (9) x3 (t) = x3 (t) x2 (t) - - x3 (t) y(t) = x1(t) A block diagram illustrating the proposed approach is reported in figure 1. The Transmitter consists of a 3D hyper chaotic oscillator and an encryption function, which is used to encrypt the message signal P(t) by means of the hyper chaotic key K(t). The Encrypted signal een(t) is superimposed with the output Y(t) of the oscillator circuit and then transmitted to the channel. The channel is assumed to be noise free and loss free. Fig. 1: System with square message signal Case 1: Channel is assumed to be noise free and loss free Fig. 2: Transmitted signal in channel Fig. 3: Message sent Vs Message received Fig. 4: System states Vs observer states Fig. 5: Error between systems states Vs observer states Case 2: Presence of small additive stochastic noise in the channel. Fig. 6: Transmitted signal in channel Fig. 7: Message sent Vs Message received Fig. 8: System states Vs observer states In this paper, a secure communication system based on Fuzzy logic observer for chaotic system is proposed to cryptographic applications. This approach combines cryptography, chaotic systems and Fuzzy observer design in Modern Control Theory. The general fuzzy models of chaotic systems were used to accomplish the design. The state feedback approach was used for designing the fuzzy observer, which is based on Takagi- Sugeno model. This approach generates transmitted signals of high complexity, which are used to transmit the message without forging the original message. This paper can be extended further to secure communications in cryptography by applying Adaptive Fuzzy Logic based designs / combined intelligent techniques. N.CHITRA has obtained B.E., (EEE) Degree from University of MADRAS in 1999 and completed her M.E (Power Systems) from Annamalai University in 2001. She is a Ph.D research scholar of Anna University, Chennai. He is presently working as Assistant Professor in department of EEE, S.K.P. Engineering College, Tiruvannamalai, India. She is a member of IETE. Her areas of interest are Soft computing, Smart Grid Power Systems and Control Systems. Dr. M. RAJARAM is Professor in Faculty of Electrical Engineering, GCT, Coimbatore, India. Previously he worked as Professor and Head in department of EEE, GCE, Tirunelveli. He has more than twenty five years of teaching and research experience. His research focuses on network security, Image and Video Processing, FPGA Architectures and Power Electronics.4.1 Classical Set Operations
11, x e B Mb(x) = k
4.2 Fuzzy Sets and Membership Functions
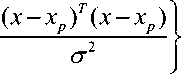
V. Defuzzification
VI. Fuzzy Observer Design: 3D-Hyperchaotic System
VII. System Overview & Simulation
VIII. Conclusion


Список литературы LMI Fuzzy Observer Design for Cryptography in Wireless Mobile Communications
- Kuang-Yow Lian, Chian-Song Chiu, Tung-Sheng Chiang, and Peter Liu , “Secure Communications of Chaotic Systems with Robust Performance via Fuzzy Observer- Based Design”, IEEE Transactions on Fuzzy Systems, Vol.9, No.1, pp.212-220, 2001.
- Tamasevicius, A. Namajunas and A. Cenys (1996), “Simple 4D chaotic oscillator”, Electronics Letters, Vol.32, pp.957-958, 1996.
- A.Tamasevicius, G. Mykolaitis, A. Cenys and A. Namajunas, “Synchronisation of 4D hyper chaotic oscillators”, Electronics Letters, Vol.32, No.17, pp.1536-1538, 1996.
- G.Grassi and S. Mascolo (1998), “Observer design for cryptography based on hyper chaotic oscillators”, Electronics Letters, Vol.34, pp.1844-1846, 1998.
- Giuseppe Grassi and Saverio Mascolo, “Synchronization of high-order oscillators by observer design with application to hyperchaos-based cryptography”, International Journal of Circuit Theory and Applications, pp.543-553, 1999.
- Tung-Sheng Chiang and Peter Liu, “Fuzzy model-based discrete-time Chiang type chaotic cryptosystem”, IEEE International Fuzzy Systems Conference, pp.1404-1407, 2001.
- P. Bergsten, R. Palm and D. Driankov (2002), “Observers for Takagi-Sugeno Fuzzy Systems”, IEEE Transactions on Systems, Man and Cybernetics-Part B: Cybernetics, Vol. 32, No.1, pp.114-121, 2002.
- Akram M.Fayaz, “Fuzzy observer-based fuzzy control of discrete-time nonlinear systems”, Michigan State university. Journal of Circuit Theory and Applications, pp.543-553, 1999.
- Kuang-Yow Lian, Peter Liu and Chian-Song Chiu, “Fuzzy model-based approach to chaotic encryption using synchronization”, International Journal of Bifurcation and Chaos, Vol.13, No.1, pp.215-225, 2002.
- Ke-Mao Ma (2002), “Observer design for a class of fuzzy systems”, Proceedings of the First International Conference on Machine Learning and Cybernetics, Beijing, pp.46- 49, 2002.
- H.F.Ho, Y.K.Wong and A.B.Rad “Direct adaptive fuzzy control with state observer for a class of nonlinear systems”, The IEEE International Conference on Fuzzy Systems, pp.1338-1343, 2003.
- Jang-Hyun Park, Gwi-Tae Park, Seong-Hwan Kim and Chae-Joo Moon (2004), “Output-feedback control of uncertain nonlinear systems using a self-structuring adaptive fuzzy observer”, Fuzzy Sets and Systems 2004.


