Load balancing in multicore systems using heuristics based approach

Published Online December 2018 in MECS

Devices like smart phones, play stations, switching routers are things of daily need in today’s life. These are portable in nature and make the best use of multicore architecture processor. Earlier, such devices used the concept of single core processor but today designers have adopted multicore processors because of their fast processing. In a multicore processor, multiple instructions are computed simultaneously on different cores hence this increases the speed of computation. Multicore processor gives the functionality of parallel processing with reduced sustainable computation time [1, 2]. Generally, multiprocessor systems are used to provide parallel environment to the system so that the processing becomes fast. However, in multicore processor, each core has its own local cache and core searches its own cache whenever it needs the data, resulting in lesser searching time compared to that required for the case of multiprocessor systems [3]. Fig. 1 shows the configuration of a single core in a multicore processor.

Presently, the primary objective of multicore processor is to divide the workload among every core of the processor such that the utilization of each core is equal or approximately equal. For a given set of tasks, the resource manager first distributes the tasks among the cores. The tasks are then scheduled on their assigned cores using any of scheduling algorithms, mostly rate monotonic or earliest deadline first scheduling algorithm. The tasks are assigned to the cores in such a manner that the load is balanced among each of the cores, so that each core is utilized equally.

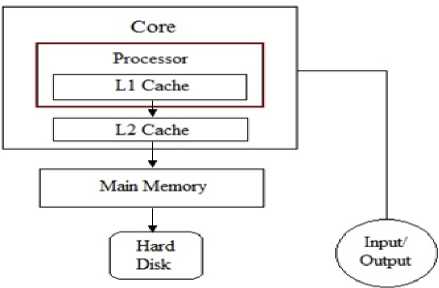
Fig.1. Configuration of a single core [3].

If the cores are fully utilized, it results in high computation speed with reduced response time. If the cores are not balanced then the tasks are migrated from highly utilized core to the least utilized core to reduce the imbalance factor amongst the cores.

Whenever a migration is to take place one has to decide about following parameters:

• •    When a task should be migrated?

• •    Which task should be migrated?

• •    Where that task should be migrated?

• •    What will be the load imbalance created amongst the cores after migration?

A load balancing algorithm for multicore system requires taking care of above questions in an optimal way. The transfer of task may reduce the imbalance factor but might add considerable migration cost. The candidate cores participating in migration process may have competitive parameters such as utilization of cores, cost etc. Further, it may be possible that a task is migrating multiple times. In this paper, a heuristic based dynamic load balancing (HBLB) algorithm is proposed that utilizes the concept of feasibility check window to balance the load amongst the cores such that the number of migrations is minimum and all the tasks meet their deadlines. The proposed paper also discuses improved heuristic based load balancing (Improved_HBLB) algorithm which is an improved version of HBLB. The Improved_HBLB aims to further reduce imbalance and the number of backtracks created by HBLB algorithm.

The paper discusses the related work in section II. Sections III and IV discusses about the system model and motivations for the proposed load balancing algorithm. The heuristic based load balancing algorithm (HBLB) is explained in section V. Improved_HBLB algorithm is discussed in section VI. Experimental results are discussed in section VII. Finally, section VIII concludes the paper.

• II.    Related Work

Many researchers have proposed different strategies to schedule the tasks and balance the workload of the system considering different areas of application [4-24]. Some application areas are load balancing in parallel computing [4], fog computing [5], cloud computing [6, 7] and real time environment [8-10, 19-24]. An efficient load balancing real time algorithm is one in which the tasks are schedulable, their deadlines are met and the load is balanced after task assignment such that the resources are effectively used with no overload or under load constraints.

For scheduling or load balancing, the tasks can be distributed to the cores using three approaches: partitioned, global or semi partitioned approach. In partitioned approach [11], tasks are assigned to cores statically and are not allowed to migrate between cores. The advantage of using partitioned scheduling is that there is no migration overhead. However, partitioned scheduling suffers from two main disadvantages. First, such schemes are inflexible and cannot easily accommodate dynamic tasks without a complete repartition. The repartitioning problem may be resolved by allocating incoming dynamic tasks to the first available core, but this may not be optimal in terms of overall system utilization. Second, optimal assignment of tasks to cores is an NP-hard problem for which polynomial-time solutions result in sub-optimal partitions.

In global scheduling policies, tasks are allowed to migrate between cores as required. Recently, several optimal global scheduling policies have been proposed [12-18]. While these schemes strive to overcome the limitations of partitioned scheduling, they add migration overhead to the tasks. In the context of real-time systems, the addition of migration overheads changes the timing behavior of tasks, thereby affecting the timing predictability of the system. A third type of scheduling approach is semi partitioned scheduling which is a combination of both partitioned and global scheduling approach. In this, first all the tasks are partitioned among the cores and if there is load imbalance amongst them, then an instance of the task is allowed to migrate from its original core to the target core.

Several researchers have proposed their algorithm which results in energy reduction by balancing the load among the cores of multicore processor. Kang and Waddington [19] proposed a Load Balancing Task Partitioning (LBTP) algorithm which aims to distribute computed load so that every core has the same amount of work. The idea behind their approach was to first apply a task partitioning mechanism that leads to good schedulability and then apply the other partitioning steps to improve load balancing test while guaranteeing a solution satisfying deadline constraints. The algorithm works in three steps by considering independent periodic tasks. The first step is to sort the tasks in decreasing order of their utilization. After sorting the tasks, the task sets are partitioned on the basis of first available cores in which they can be fit such that the utilization of each core is less than or equal to one. In the last step, the tasks in the cores are repartitioned or reassigned to the core with least utilization in order to reduce the imbalance among the cores. However, the major limitation of this approach is that in the second step, the algorithm is creating the load imbalance itself and in the third step, it is reducing the imbalance created by the task assessment of second step. Thus, this would result in unnecessary increase in the migration overhead when the algorithm is made to run in dynamic cases.

In one of the load balancing algorithm given by Park et al. [20], partitioning of the tasks was used to adjust the number of active cores to optimize the power consumption during execution. It migrates the tasks from the core with highest utilization to the core with lowest utilization considering the fact that utilization of each core should be less than or equal to one. The algorithm works in two phases: dynamic repartitioning and dynamic core scaling. The first phase uses the concept of dynamic power and dynamic utilization to reduce the dynamic energy consumption. The second phase reduces the number of active cores by switching off the cores thus, reducing the leakage energy. If the number of cores in sleep mode is more than the required and increase in frequency does not result in effectiveness, this means that the cores' utilization is wasted and it is not beneficial to use large number of cores. It also uses the fact that a task once migrated to a foreign core can be further migrated to other core, if necessary. Thus, this would result in unnecessary migrations and hence increases the migration overhead.

March et al. [21] proposed two algorithms- Single Option Migration (SOM) and Multiple Option Migration (MOM). They allowed task migration, to reduce energy consumption in multicore embedded systems with realtime constraints, by implementing Dynamic Voltage Frequency Scaling (DVFS) capabilities. As the name suggests, SOM checks a single target core before performing a migration while the MOM searches the optimal target core. Their work was focused on multicore processors where the scheduler includes a partitioner module to distribute tasks among the cores. This partitioner readjusted all possible workload imbalances at run-time that may occur at arrivals or exits of tasks by applying task migration. The algorithm is applied at three variants of time: when a task arrives, when a task leaves the system and in both cases. They have considered maximum of 4 cores and frequency levels up to 8. The main contribution of their work is that the assignment of tasks to the cores is done without sorting the tasks in decreasing order of their utilization which may reduce the number of migrations and further may reduce the migration over head of the system. The number of cores considered by March et al. [21] for experimental setup was very less as compared to present use of large numbers of cores in multicore processors.

The work of Cho et al. [22] included a Power and Deadline Aware Multicore Scheduling (PDAMS) to balance the consumption of load and save power. The deadline aware load dispatch algorithm works at two levels. The concept of load imbalance is at first level while the novel load balancing strategy distribution of task's deadline is at the second level. The tasks are assigned to the cores on the basis of deadline uniformity. The authors demonstrated that static power can be saved by switching off the cores once they have finished the execution of tasks assigned to the cores. The major shortcoming of their approach was that the algorithm allows the tasks to finish after their deadline. The processing speed increases when the deadline is missed so that the tasks can be finished faster. Further, missing of the deadlines of the tasks leads to an increase in the response time. If the tasks, which have missed their deadlines, are re-executed at higher frequency levels then this would result in higher energy consumption.

Based on the previous research works as reported above on the load balancing strategies the main issues to be addressed are:

• •    when and which task should be migrated

• •    decision of destination core

• •    cost effective migration and balancing of cores

Thus, load balancing of multicore processor is necessary from the point of view of increased utilization such that each core is fully utilized and the system results in increased performance with good response time. The next section discusses the system model for the proposed

Heuristic Based Load Balancing algorithm (HBLB) in detail.

• III.    Proposed Model

This section deals with the assumptions, terms used and the system model considered in this paper.

• A.    Assumptions

Following considerations are used in this paper:

• •    Assume a multicore system with a set of independent tasks.

• •    Tasks are periodic in nature i.e. they tend to repeat themselves after a certain interval of time.

• •    Consider dynamic priority scheduling algorithm Earliest Deadline First (EDF).

• •    All overhead for scheduling and context switching considered negligible.

• B.    Terms Used

The symbols and terms used in this paper are summarized in Table 1 given below:

Table 1. Symbols and Terms Used

Terms	Meaning
C	Set of cores in the multicore system consisting of M number of cores
7	A core from core set C where j=1 to M
T	A task set consisting of N tasks
T ,	A task from task set T where i = 1 to N
et	Worst case execution time of the task T ,
p ,	Period of task T ,
D ,	Absolute deadline of the task T ,
u ,	Utilization of task T ,
«	Utilization of core C ,
« tot	Total utilization of the multicore system
Н ткЛ	Heuristic value of task Tk in FCW against core C ,
^.i	Maximum imbalance created by task T k in FCW when assigned to core C ,
Dk	Absolute deadline of the task T k in FCW
W	Weight factor
FCW	Feasibility check window
FT	Feasibility task window

• C.    System Model

Consider a multicore system C with M number of processing cores such that C= {C1, C2 ,C3 ,..., CM} and a set of real time tasks T = {T1, T2 ,T3 ,..., 7^} where N is the total number of tasks in the task set T. These tasks are periodic in nature and there is no task dependency. Each task 7 in T is represented as (e,, p,, d,) where e, is the worst case execution time of the task T,, p, is the period of the task T, after which T, will repeat itself and d,is the relative deadline of the task T, which is equal to the period p, of the task T,. The tasks are scheduled with earliest deadline first scheduling algorithm on a multicore processor system where the tasks are assigned priorities on the basis of their absolute deadlines. Closer the deadline, highest is the priority of the task [23]. Each instance of the task is called a job and the kth instance of task Tt is denoted as Ttik. A task set is said to be feasible if all the jobs meet their deadlines.

The utilization of the task T_t is given by U_t = e_t/p_t and the total utilization of the task set T is given as:

the cores. The dispatcher has to ensure that all the cores have equal amount of workload and the difference between utilization of cores should be minimum. The job of dispatcher is also to update the scheduler of the cores in parallel whenever new task or a task at its period arrives to the system.

N

Ut = У Ui

Ti i=1

When the tasks are allocated to cores of the multicore processor then the utilization of a particular core Ci is summation of utilization of all the tasks assigned to that core and is denoted as:

U C = У Ut.               (2)

T e C i

The total utilization of the multicore system is summation of utilization of all the cores,

M

U tot = y U C                 (3)

j = 1

One necessary condition that should be observed for the task set to be schedulable is that the total utilization of the multicore system should not be greater than the number of cores and the utilization of each core should be less than or equal to one, i.e.

U tot <  M ; U C <  1                (4)

If equation (4) is not satisfied, generating a feasible schedule by the multicore processor is not guaranteed. All the tasks scheduled on a particular core satisfying (4) may guarantee a feasible schedule.

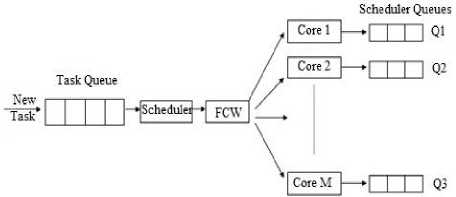
Fig.2. Parallel execution of scheduler and core using FCW.

Fig. 2 shows the system model of the proposed approach. The input to the task system model is the set of real time periodic tasks set T. All the tasks in the task set T arrive at the dispatcher from where they are partitioned among the cores of the multicore processor for their execution. Each core has its own scheduler where the task one assigned to the cores are scheduled and executed using earliest deadline first scheduling algorithm. The dispatcher is responsible for balancing the load amongst the cores of the system and hence it applies the load balancing algorithm to assign the tasks in the task set to

• IV.    Motivational Example

A large number of components in a system may result in more power requirement. Power of the multicore system can also be decreased if all the cores of the system are fully utilized and they are least imbalanced. Now-a-days, multicore processors are preferred as all the functionalities are embedded in a chip and the reduced chip area would result in reduction of power supplied to the chip and also increase the efficiency and speed of the system. Hence, an attempt has to be made for balancing the load of cores of the multicore processor. There are two situations that lead to motivate for the proposed work. These are the assignment of tasks and balancing of the load among the processor of the multicore system when the cores are underutilized or when the cores are normally utilized.

• A.    Cores are underutilzed

Consider a multicore processor with three cores and a set of periodic task set T with task utilization as U 1 = 0.3, U 2 = 0.2, U 3 = 0.2, U 4 = 0.1 and U₅ = 0.1. The tasks are sorted in decreasing order of their utilization and are assigned to the first available core [21].

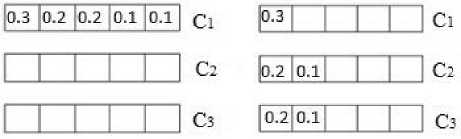
Fig.3. Imbalanced cores and balanced cores.

From Fig. 3, it is clear that the approach is creating an imbalance amongst the cores as core C 1 is fully utilized and cores C 2 and C 3 are having zero utilization. This is because when the tasks in the task set are sorted in decreasing order of their utilization and if the utilization of all the tasks in the task set are very small then in such cases all the tasks can easily be assigned to the first available core and hence the remaining cores remain unutilized which is an underutilized situation. A remedy to the above problem is that tasks are assigned to the core with least utilization. Whenever a task arrives the system, the core with least utilization is checked and the task is allocated to that core as shown in Fig. 3.

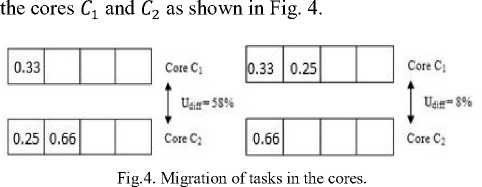
• B.    Cores are normally utilized but imbalance exists

The solution given in Fig. 3 also suffers from certain limitations. Consider another task set T1, T2 , T3 with utilization as U1 = 0.33, U2 = 0.25 and U3 = 0.66. The tasks are assigned to the least utilized cores [19, 21] and it can be seen that the cores suffers imbalance amongst them as explained in Fig. 4. First, the task with utilization U1 is assigned to core C1 then task with utilization U2 to core C2 as its utilization is small. The task T3 is then assigned to the core C2 as it has least utilization. As soon as T3 is assigned to core C2, the utilization of core C2 is 0.91, and the difference between core C1and core C2 is 58% which is more than the default threshold [24] assigned to the kernel, which is either 0.25 or 0.33. Thus, migration is required in order to reduce the load imbalance between

Another load balancing strategy of task assignment amongst the cores was discussed in PDAMS [22]. According to PDAMS algorithm, it distributes the tasks on the basis of deadline uniformity. More uniform the distribution of task deadlines is, the lower is the missingdeadline probability. The variance of task deadlines was used as the feature of deadline distribution. Smaller variance of task deadlines implies that the time slot between two task deadlines is shorter. The drawback of their algorithm is that it allows the tasks to finish after their deadline and missing of the deadlines of the tasks leads to an increase in the response time.

The above examples make it very clear that the workload difference among the cores should be minimum else imbalance exists and migration of tasks may take place. If the number of migration increases, migration overhead increases and this would finally increase the expense of the system. Thus, this motivates to propose a load balancing algorithm that reduces the imbalance as well as the migration of tasks among the cores.

• V.    Heuristics Based Load Balancing

This section discusses the heuristic based load balancing (HBLB) algorithm which uses the concept of heuristics to balance the load among the cores of the multicore systems. The HBLB algorithm uses a function which calculates the heuristics for a set of tasks in FCW. In other words, the heuristics function is computed for each task lying in the window. The size of feasibility check window simply says that how many tasks are required to compute the heuristic function for each selection of best suitable task. Larger size of feasibility check window gives better opportunity to select more suitable task whereas less suitable task is selected for the case of smaller size of feasibility check window. Further, larger feasibility window size requires larger computation overhead than that compared with smaller one. The proposed heuristic function is a function of imbalance factor among the cores and deadlines of the tasks in FCW and is given below in expression (5):

H^ = 4 + D k / W          (5)

where, H_Tlk is the heuristic value for a task T_k , I_T is the maximum imbalance among the cores when a task T_k will be assigned to a core Q, D_k is the absolute deadline of the task T_k and W is the weight factor. The weight factor decides the dominance between imbalance and deadline of the task while computing the heuristic function of the task.

The tasks in the task set are ordered in increasing order of their deadlines using earliest deadline first (EDF). In deadline based ordered task set, heuristic function is computed for first K tasks, where K is the size of feasibility check window and select the best suitable task decided on the basis of heuristic function, from K tasks. The selected task is assigned to the respective core and window size is moved by one. With this new task in window, heuristic function is computed again and the suitable task is selected. The forward process is repeated until either of these conditions is met,

• 1)  Window is empty, or

• 2)  A selected task becomes infeasible.

In case a task becomes infeasible, it backtracks to the previous selected task level and looks for next suitable task. The algorithm repeats this forward and backward operation until either,

• 1)    Task set is feasibly scheduled, or

• 2)    All the possible search space of the tasks selection is exhausted.

Suppose a task set T has N number of tasks such as: T= {T 1 , T 2 , T₃, ...,T_N }. The tasks are arranged in non decreasing order of their deadlines and the tasks in feasibility check window are {T 1 , T 2 , T₃}, considering the size of feasibility check window equal to 3. The heuristic for all the three tasks is calculated using (5) against the M cores. The imbalance I_T in (5) calculates the maximum imbalance created in all other cores other than C [ when task T_k is assigned to core Q . Let the imbalance is checked for task T 1 against the core C 1 . The utilization of core C 1 , when task T 1 considered for partitioning will be:

Uc = Uc + Ut              (6)

The imbalance created between C 1 and each core selected from remaining M-1 core is computed as (7) where m= 2 to M:

I T . = U i- U C . I                (7)

Out of these M-1 imbalances computed for each pair of cores, (C 1 , C_m), the maximum imbalance is selected as:

IT, к = max( I\2, IT,3, IT^,---, IT,M )(8)

Using this maximum imbalance factor, the heuristics of the tasks in feasibility check window is calculated using (5). The heuristic function of task T 1 against core C 1 is:

HTU = I^ + (Ц/ W)(9)

Similarly the heuristic of task T 1 against core C₂ is:

Ht2 = Itu + (Д/ W)(10)

Likewise, the heuristic function is computed for all the tasks T 1 , T₂, T₃ in feasibility check window against all the cores and the heuristic function with minimum value is selected, as is given in (11):

H(T ) = min( H_T , H_T ,...,H_T , H_T , H_T ,...,

T1,2      T1,3            T1,M      T2,1

H ,H ,H ,  ,H )(11)

T2,M     T3,1     T3,2

Suppose the minimum value of heuristic obtained from (11) is Н_{Тз 2} then the task T₃ will be assigned to core C₂ .

Algorithm 1 Heuristic Based Load Balancing (HBLB)

• 1.    Arrange the tasks in non-decreasing order of their deadlines.

• 2.    For all tasks in FCW calculate heuristics using equation (5).

• ^3.     Н_Т^, , = min (H_Tki) where H_T   is the best

• 4.    Allocate the task T_k ' to core C_t .

• 5.    If utilization of all cores is greater than 1.0 then

• 6.         Backtrack to previous search level.

• 7.         Extend the partitioning by selecting the task

• 8.    Repeat step 5 until task set is feasibly scheduled or all the possible search space of the tasks are exhausted.

• 9.    Increment the size of FCW by 1.

• 10.    If all the tasks are assigned then

• 11.        If imbalance > 0.33 then

• 12.            Backtrack to previous search level.

• 13.            Extend the partitioning by selecting the

• 14.         Else

• 15.             Partition successful.

• 16.    Else

• 17.        Go to step 18.

• 18.    Repeat steps 2 to 16 until termination condition is met.

heuristic value for all k tasks in FCW against I^th core for k=1 to K and i= 1 to M.

having the next best H value.

task having the next best H value.

As soon as a task is assigned to a particular core based on the best heuristic value, the size of feasibility check window is incremented by 1. With this new task say T4, the feasibility check window now has T2, T3, T4.

Again the heuristic value is computed for all the tasks against all the cores so the next core can be selected. Thus, the heuristic function can be generalized as (12) where k is the number of tasks in feasibility check window and M is the number of cores, HQT j,/ ) is heuristic for a task T j selected for allocation to core I' is given in (12):

^H(T j , t ) = ^min( H T 1,₂ , ^H T 1,₃ , • • •, ^H T 1, _M , ^H t ₂ , ₁ , ^H t ₂ , ₃ , • • •,

H , H , H ,  , H )           (12)

^T 2, M     ^TK ,1      ^TK ,2           ^TK , M

The HBLB algorithm backtracks to the previous level in the case when a task cannot be assigned to any of the cores as the utilization of a core is more than the feasible condition of the tasks to schedule, that is, U >1. Once the algorithm is backtracked, the next best minimum value of heuristic is selected and the partitioning process is extended.

The termination condition of HBLB algorithm is either:

• 1)    all the tasks are scheduled or

• 2)    all possible search space of the tasks selection is exhausted and no more backtracking is feasible.

The algorithm clearly shows that once the heuristics for the tasks in the FCW are computed, the task with best heuristic value is assigned to the core for which the best value is obtained. After assignment of best task, load imbalance is checked out against the default set threshold. If the imbalance between the two cores is more than 0.33 [24], migration of task is performed. If the best task allocated to the core does not reduce the imbalance after the migration process, the algorithm backtracks to previous search level and selects the task with next best heuristic (H) value in FCW. The pseudo code of HBLB approach is discussed in algorithm 1.

Table 2. An Example

Tasks	Execution Time	Period	Deadline	Utilization
T 1	2	6	6	0.33
T 2	1	12	12	0.083
T 3	2	12	12	0.17
T 4	2	4	4	0.50
T 5	3	4	4	0.75
T 6	2	7	7	0.29

Table 2 shows a task set consisting of six tasks, each of it with their execution time, period, deadlines and utilization. Suppose the number of cores is 3. The ordering of tasks in increasing order of their deadlines will be T₄,T 5 ,T₁,T₆,T₂,T₃ . The size of FCW is equal to number of cores, which is 3. Initially, the FCW contains tasks T₄, T₅,T₁. The heuristics for all the tasks is calculated against core C 1 , C₂, C₃ ; and H_t j represents the heuristic of task T_t on core C j .

After calculating heuristics, the minimum heuristic H 11 is selected and task T 1 is assigned to core C 1 . The FCW is then increased by one and it now contains tasks

T₄,T₅ and T 6 . Again, the heuristics is calculated for these three tasks in the FCW and task with minimum heuristic is selected, which is H 62 in this case. This process is continued till all the tasks are assigned to the cores and imbalance is less than 0.33. It can be seen from Fig. 5 that all the tasks other than T₅ are assigned to the cores and T₅ cannot be fit in any of the cores.

Thus, the algorithm backtracks to previous level when FCW has T 2 and T₅ (Fig. 6). It then selects the heuristic with next minimum value. Again, task T 2 is selected and T₅ will again become infeasible (Fig. 7). The algorithm then backtracks to level where FCW have T₅, T 2 and T₃.

It then selects next minimum heuristic value, which is H₂₁. The selection of task T 2 will again further make T₅ infeasible. Thus, the algorithm now backtracks to the level where T₄, T₅ and T 2 are in FCW (Fig. 8). The HBLB algorithm now selects the next minimum heuristic value at this level, which is H₅₃. So, task T₅ is assigned to core C₃. Now, FCW have T₄, T 2 and T₃.

The process of calculating heuristics, selecting minimum heuristics and assigning appropriate task to the core is continued until all the tasks are assigned to the cores and the load amongst the cores is balanced (Fig. 9).

Fig.5. Example showing selection and allocation of best heuristic value task.

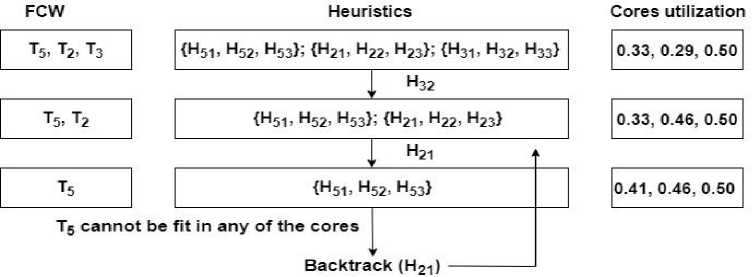
Fig.6. T ₅ become infeasible and the process backtracks.

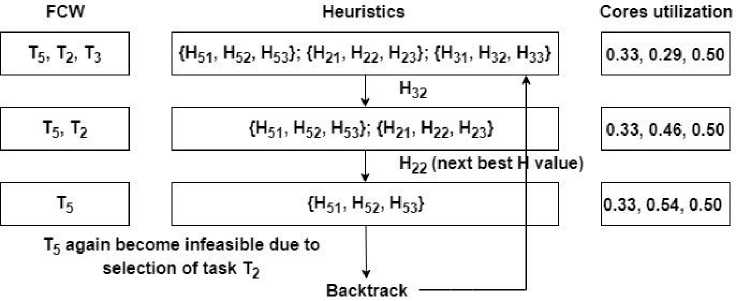
Fig.7. Selecting next best value, T ₅ again become infeasible and process backtracks.

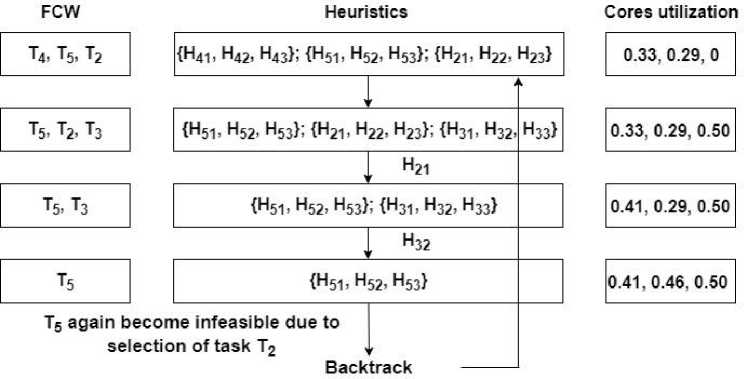
Fig.8. Process backtracks to one level up and selects next best value.

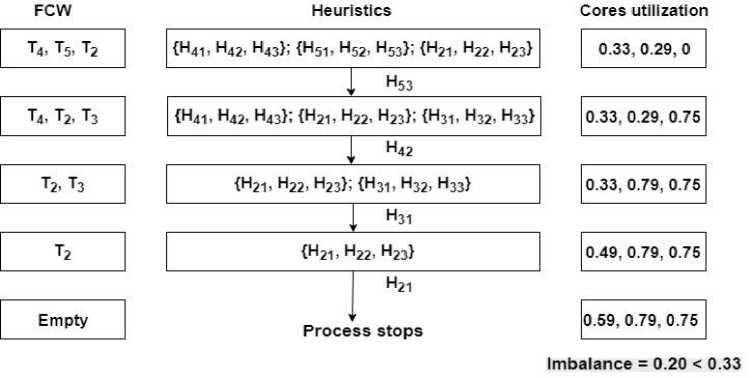
Fig.9. All tasks are assigned to the cores.

Thus, it could be seen that the maximum imbalance among core is 0.20 whereas the same example when tested for LBTP and PDAMS gives an imbalance of 0.63 and 0.79 respectively with six backtracks in LBTP and one infeasible task in PDAMS. If in this example, after assigning all the tasks to the cores, imbalance exists the algorithm again backtracks level by level such that the imbalance can be reduced.

• V I. Improved_Heuristic Based Load Balancing

Heuristic based load balancing algorithm (HBLB) is a useful concept for gaining minimum imbalance than to allow more number of migrations and backtracks. Although, the simulation results in section VII shows that the imbalance factor among the cores generated by HBLB algorithm is less than the algorithms LBTP and PDAMS for different parameters but there are certain limitations with HBLB. These limitations are as follows:

• •    Infeasible task carry forward assignment algorithm.

• •    Even if a task is not feasible for a particular core, HBLB approach still calculates the heuristic function for it.

• •    Level by level backtracking is done when cores are not balanced or a task becomes infeasible, in which some cases are left out.

• •    Backtracking is done with no guarantee of rebacktracking.

• •    Increases computation cost and complexity.

Whenever a task gets infeasible, the HBLB algorithm checks for the feasibility of other tasks in FCW and assign them to the suitable cores. In this way, the infeasible task remains in the FCW till the last level where all the tasks other than this task are assigned to the cores of the system. This causes unnecessary backtracking from last level. Another limitation is that when a backtracking is performed, the HBLB checks for a feasible solution at every predecessor level. This increases the computation cost because at every previous level the core are checked in order to make the infeasible task feasible. This can be avoided if via some condition it could be known priory as up to which level the algorithm should be backtracked such that the infeasible task can be made feasible. Previously, the algorithm backtracks when a task is infeasible on a core. Other than these limitations some more conflicts must be taken into account such that the feasibility of the tasks in the task set can be guaranteed. These conflicts can be:

• 1.    Conflict 1: A task X is feasible for a single core C and heuristic function selects some other task, the task X gets infeasible in future.

• 2.    Conflict 2: More than one task is feasible for a single same core (Say C).

• 3.    Conflict 3: Two tasks (T 1 , T₂) are feasible for two different cores ( C 1 , C₂) respectively but the heuristics selects a third task (T₃) which occupies any of cores C 1 or C₂ making the task set infeasible in further steps.

• 4.    Conflict 4: A task is not feasible for any of the cores.

In regard of these conflicts, a remedy is to be find out, which may be checking the feasibility of each core at every FCW level. For conflict 1, the task X is assigned to that only core C for which it is feasible reducing the chances of infeasibility and backtracking. If any of the conflicts 2, 3 or 4 occurs in the task set, backtracking is done. But the backtracking should include following points to avoid level by level backtracking: (a) Level up to which the tasks are backtracked and (b) this new path guarantees that same infeasible situation will not occur in future for same path when new tasks arrives in FCW?

For these questions, it can be justified as the level up to which this backtracking should be done will be that level for which all tasks are feasible for all the three cores and no conflicts have aroused. Once backtracked to that level, a combination of the infeasible task and core is selected for which core fragment is minimum. The main idea behind the selection of least fragment value is that while assigning the tasks to the cores, the cores with such minimum fragments are not selected and hence are left out causing the task set infeasible. Selecting the least fragment valued core minimizes this problem of fragmentation. This can be easily understood using Improved_HBLB algorithm shown in algorithms 2, 3 and 4, followed by an example which explains how the Improved_HBLB algorithm rectifies the limitation observed in HBLB.

The termination condition of Improved_HBLB is either:

• 1)    all the tasks are scheduled, or

• 2)    all possible search space of the tasks selection is exhausted and no more backtracking is feasible

The Improved_HBLB algorithm is similar to the HBLB algorithm except that in Improved_HBLB, there is a feasible task (FT) window for every task in FCW. The FT window keeps track of all the feasible cores where the tasks can be fit at a particular level such that the utilization of any core is less than or equal to 1. The FT window makes a check on the conflicts discussed previously in this section and handling them in Improved_HBLB. The Check_Heuristic() function, in algorithm 3, checks for a condition when two tasks are feasible for two same set of cores. In such case, if the selected task core combination is different from these two tasks and the selected core is anyone of these two cores in the set then it is guaranteed that any of the two tasks will become infeasible in future. So, the algorithm backtracks.

Algorithm 2 Improved_Heuristic Based Load Balancing (Improved_HBLB)

• 1.    Arrange the tasks in non-decreasing order of

• 2.     If Utilization(System) <= M then

• 3.        Go to step 6.

• 4.     Else

• 5.        Task set is infeasible.

• 6.    Add K tasks to FCW.

• 7.    For all tasks in FCW, update FT[] against

• 8.     New_utilization (C_tJ ) = U(T_j) + U(C , ) for all i

their deadlines.

every core C ^ .

• = 1 to M and j= 1 to K.

• 9.    If New_utilization ( C ^j ) <= 1 then

• 10.     Add C_tJ to FT j [].

• 11.    If FT j [] == NULL then

• 12.     Backtrack.

• 13.    Else if FT j [] has a single core entry (Say C) then

• 14.     Assign the task T j to core C without

• 15.    Else if two or more tasks in FT[] are feasible for same core C then

• 16.     Backtrack.

• 17.    Else if FT_x[] and FT_y[] (for two tasks T_x , T_y) have same entery for two core C_a and C_b then

• 18.     Go to step 13.

• 19.     Check_Heuristic (FCW, FT x [], FT y []).

• 20.    Else

• 21.     Calculate heuristics for the tasks in FCW.

  
  

  ^Нт к У ‘

  
  

calculating heuristics.

min (нТк?) where Нт   is the best heuristic value for all k tasks in FCW against Ith core for k=1 to K and i= 1 to M .

Allocate the task T_k - to core C , .

Maintain a record of cores' utilization at every level of assigning tasks.

If utilization of all cores is greater 1.00 i.e. the tasks becomes infeasible then

Backtrack to previous feasible level.

Repeat step 8 to 22 until tasks set is feasibly scheduled, or

All the possible search space of the tasks selection is exhausted.

Increment the size of feasibility check window by 1.

Repeat steps 2 to 29 until termination condition is met.

Algorithm 3 Check_Heuristic(FCW, FT x , FT y )

• 1.    If minimum heuristic selected is H_T^ ^ and k ' ^

• 2.   Backtrack(FCW).

• 3.    Else

• 4.   Go to step 23 in Improved_HBLB algorithm.

T_x or T_y and i= C_x or C_y then

Algorithm 4 Backtrack(FCW)

• 1.    Using step 24, find a level L at which all the tasks in FCW are feasible for all core C [ where i=1 to M.

• 2.    Backtrack to level L .

• 3.    Select the task in FCW for which fragmentation among the cores is minimum, say for T_p core C_q .

• 4.    Assign the task T_p to core C_q.

• 5.    Go to step 7 in Improved_HBLB algorithm.

Now, consider the same example as discussed in section V using Improved_HBLB approach. At level 2, when FCW have T₄, T₅ and T 2 , the FT[T₅] has an entery of C₃ which means that the task T₅ can only be feasible on core C₃. So, at this level the task T₅ is assigned to core C₃ and FCW now contains T₄ , T 2 and T₃. The Improved_HBLB gives same imbalance for this example as of HBLB but considering the number backtracks required, the HBLB algorithm has three backtracks whereas Improved_HBLB algorithm reduces this number to zero. This shows that Improved_HBLB is an improvement over HBLB on the basis of number backtracks, number of infeasible tasks and in some cases in terms of imbalance also.

• VII.    Simulation Results

To evaluate the performance of proposed heuristic based load balancing, it has been compared to the two well known approaches: LBTP, in which tasks are scheduled such that the load balancing is maintained, and PDAMS, in which the tasks are assigned to the cores on the basis of deadline uniformity. The load imbalance is evaluated using equation (8). Every task set is generated randomly on the basis of execution time and period range. The execution time of tasks ranges from 1 to 50 and the period of the tasks ranges from 1 to 100. The relative deadlines of the tasks are equal to their periods. The simulation parameters are discussed in Table 3. The number of tasks in the task set is not restricted.

Table 3. Simulation Parameters

Parameters	Value
Execution time	[1, 50]
Period	[1, 100]
Number of cores	03
Size of FCW	03
Weight Factor (W)	11
Imbalance allowed	0.33

The algorithm HBLB is not core dependent and hence the number of core does not affect the outcome of the result. However, if the number of cores is more, the size of the feasibility check window increases equal to the number of cores and hence, the look ahead nature of the algorithm will be improved. So, for the ease of comparison, only three cores are considered for result computation.

The experimental results for proposed study are discussed under following points:

• A.    Effect on imbalance created amongst the cores:

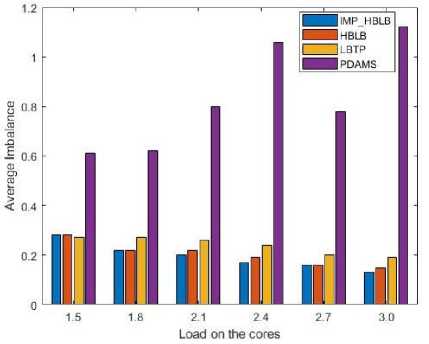
Fig.10. Comparison on the basis of average imbalance v/s system load.

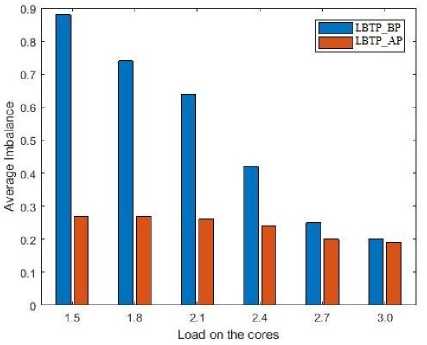
Fig.11. Imbalance in LBTP approach before and after partitioning of tasks.

The algorithms HBLB, Improved_HBLB, LBTP and PDAMS were tested on the same task sets generated randomly. Fig. 10 shows the average imbalance amongst the cores with respect to the system load, when the system load is varied from 1.5 to 3.0. From Fig. 10, it can be seen that PDAMS creates maximum imbalance amongst all the four approaches and as the system load increases HBLB and Improved_HBLB performs better than LBTP generating minimum possible imbalance amongst the cores. Thus, for M=3, HBLB and Improved_HBLB gives an improvement of 15% and 23% over LBTP respectively and 72%, 75% over PDAMS respectively. Also it can be seen from Fig. 11, that the LBTP algorithm is first creating an imbalance and then correcting it, which reduces the overall efficiency of the

LBTP algorithm.

• B.    Effect on number of backtracks:

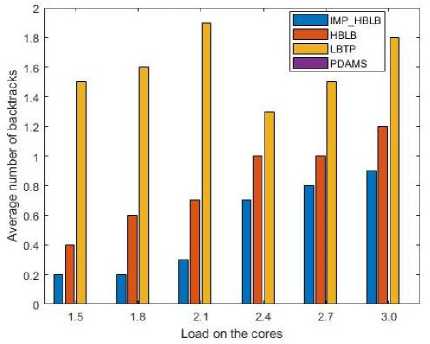
Fig.12. Comparison on the basis of number of backtracks v/s system load.

Another parameter for which algorithms were tested is the effect on number of backtracks when the system load is varied from 1.5 to 3.0. The PDAMS algorithm does not use the concept of backtracking and hence, it has zero number of backtrack. From Fig. 12, it can be seen that Improved_HBLB requires least number of backtracks when compared to HBLB and LBTP. Thus, in regard of backtracks, Improved_HBLB gives an improvement of 57% and 84% over HBLB and LBTP whereas HBLB algorithm gives an improvement of 63% over LBTP.

• C.    Effect on number of infeasible tasks:

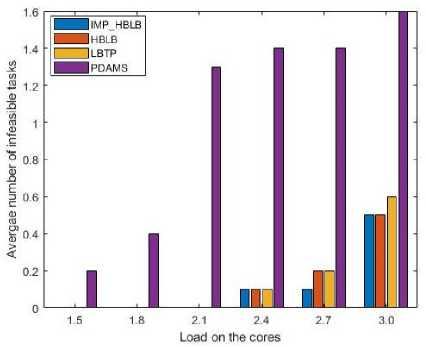
Fig.13. Comparison on the basis of number of infeasible tasks v/s system load.

In a hard real time multicore system, it is important that that all the tasks are assigned to the cores and when executed, meet their deadlines. Hence, the other parameter on which the efficiency of an algorithm can be judged is the number of infeasible tasks left out when the system load is varied from 1.5 to 3.0. From Fig. 13, it can be seen that in PDAMS, maximum number of tasks are getting infeasible as compared to the other three algorithms. The Improved_HBLB gives the best results amongst the four approaches. The reason is that Improved_HBLB uses the concept of FT window that keeps a track on feasibility condition for every task in FCW.

• D.    Effect of weight parameter W:

The heuristic function value depends on value of W. Fig. 14 above shows the variation in imbalance among the cores for different values of W. For utilization from 0 to 1, it can be seen that the value of imbalance is constant for all the value of W.

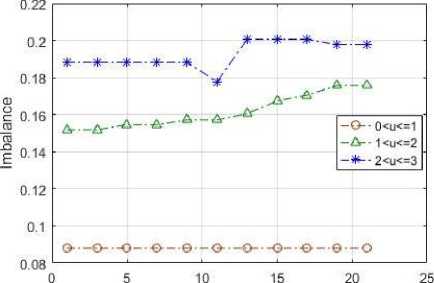
Weight (W)

Fig.14. Imbalance variation of HBLB on different values of W and utilization from 0 to 3.

When the utilization ranges from 1 to 2, then with increase in W, imbalance amongst the cores increases. When the utilization of the system is varied from 2 to 3, it can be seen from Fig. 14 that the average imbalance first decreases and then increases providing a minimum imbalance at W=11, which is the midpoint in the range considered for W.

• E.    Performance of HBLB and Improved_HBLB:

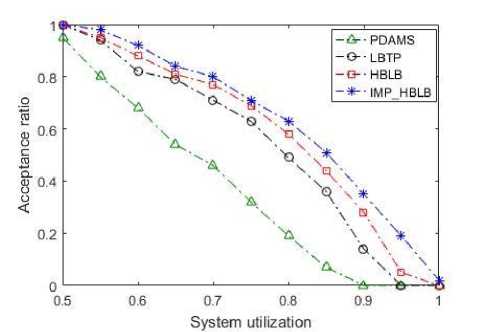
Fig.15. Performance of HBLB and Improved_HBLB approach when system utilization is varied from 0.5 to 1.0.

The parameter considered for measuring and comparing the performance amongst the four approaches will be acceptance ratio. Acceptance ratio is the ratio between the tasks sets that are scheduled by the total number of task sets considered during the experiments. The task sets are generated randomly for total system's utilization of 0.5 to 1.0 with a step size of 0.5. The tasks' utilization is varied from 0.1 to 1.0. Over 500 experiments were made to run for each case and the results are shown in Fig. 15. It can be seen from Fig. 15 that the tasks' maximum utilization is varied. A variation in task's maximum utilization is inversely proportional to the number of tasks generated in the task set and it leaves the algorithm with a lesser choice of selection of tasks. In other words, if maximum utilization of tasks is increased then the number of tasks generated in the task set will be less. Due to this reason, it can be seen from results that as the maximum utilization of the tasks increases the performance of all the approaches degrades. However, for every case discussed above, it can be seen that HBLB and Improved_HBLB approaches works better than the other two approaches and has a better performance over LBTP and PDAMS approaches.

• VIII.    Conclusions

The main goal of real time load balancing algorithm is meeting the deadlines of the tasks and to increase the utilization of the cores which indirectly increases the utilization of the system. Many algorithms are present in the literature that provides such functionality. However, to reduce the load balance among the cores, the tasks are migrated from one core to another and this may result an increase in cost of the algorithm. Prior selection of optimal task using look ahead feasibility check window is an intermediate solution which assigns the best task to the cores that reduces workload of the system as well as the migration of the tasks. In this paper, a heuristic based load balancing algorithm (HBLB) is proposed for dynamically balancing the load in real time multicore systems. HBLB reduces the imbalance amongst the cores but it also faces some limitations. These limitations were solved by Improved_HBLB algorithm which is an improved version of HBLB algorithm. Through simulation studies, it is demonstrated that heuristic function is a useful concept for gaining minimum imbalance than to allow more number of migrations and backtracks. The simulation results show that the imbalance factor among the cores generated by Improved_HBLB and HBLB algorithms is less than the compared algorithms of LBTP and PDAMS for different parameters. From simulation analyses, following results are drawn:

• •    For a utilization between (0,M], the Improved_HBLB and HBLB algorithm gives better results than LBTP and PDAMS in terms of balancing workload amongst the cores.

• •    The impact of backtracks is less as compared to that in LBTP. This clearly indicates that the cost of algorithm is less in terms of migration overhead.

• •    Improved_HBLB algorithm provides better results than HBLB, LBTP and PDAMS, thus, reducing the overall number of migration of tasks from one core to another.

• •    The success ratio of the tasks in Improved_HBLB and HBLB is more as compared to that in LBTP and PDAMS algorithms.

• •    The different values of W predicted that the value of imbalance remain ineffective when total system utilization is less than 1 and after it as the value of W increases, the imbalance increases.