Логики с векторной семантикой как средство верификации баз знаний

Знаниевое моделирование сегодня – один из основных способов описания трудноформа-лизуемых предметных областей (ПрО). Не обладая сопоставимой с традиционным математическим моделированием предсказательной силой, неся в себе существенную долю субъективизма, оно, тем не менее, применимо всюду, где возможно человеческое суждение. Это делает его универсальным, хотя и ограниченным по возможностям инструментом описания любых выразимых словами сущностей. Несмотря на известную критику (см. напр. [1, 2]), альтернативы им пока не видно. Если традиционные математические (и не только) модели отражают свойства и отношения непосредственно ПрО, знаниевые модели отражают представление эксперта о ней. Это отдаляет их от исходного предмета, но позволяет использовать там, где другие подходы невозможны или малопригодны.

Сегодня известно несколько основных подходов к знаниевому моделированию. Каждый из них опирается на соответствующую модель знаний: сетевой, логический, продукционный, фреймовый [3]. Продукционный подход наиболее удобен в силу своей внешней простоты, модульности, «понятности» для человека. Он позволяет гибко перенастраивать модель, вводить в неё новые сущности и единицы знаний, хорошо подходит для организации (логического) вывода. Продукционное моделирование по своим выразительным возможностям со- поставимо с универсальными алгоритмическими моделями [4]. В то же время знаниевые модели, имеющие вид баз знаний (БЗ), особенно логические и продукционные, могут нести в себе артефакты, снижающие или вовсе обнуляющие их ценность [5]. Появление таких артефактов может быть обусловлено субъективным характером моделей, результатом технических ошибок, иными причинами. В любом случае необходимо предусматривать проверки соответствующих БЗ на полноту, достоверность, непротиворечивость и иные «не-факторы» [6, 7], или хотя бы уверенно учитывать их с помощью соответствующих процедур. Причём, принимая во внимание большие размеры возможных БЗ, такие проверки должны по возможности проходить в автоматическом или автоматизированном режиме.

На сегодняшний день используются два основных подхода к продукционным моделям: на основе классической логики и на основе нечётких логик и множеств. Классическая логика плохо приспособлена для работы с указанными артефактами. Используемые в ней знания и факты должны быть строгими, точными, достоверными. Работая в категориях Истины и Лжи, она не допускает неполноты и противоречивости данных и знаний. Источникам данных приходится доверять или отвергать их, что затрудняет её использование в реальных ПрО.

Нечёткая логика лучше приспособлена для работы в реальной обстановке, когда сведения поступают из разных источников, могут противоречить друг другу, быть недостаточными, иметь разную степень достоверности и т.п. Последнее обусловлено более сложным представлением истинности. Вместо множества {0, 1} - {Ложь, Истина}, здесь используются её степени от 0 до 1 в виде рациональных дробей, лингвистических термов или просто отрезка [0, 1], либо его аналогов: [-1, 1], [-100, 100], [0, 100] и т.п. Это позволяет выразить сомнение в тех или иных сведениях, учитывать их неполноту, работать с противоречиями. Но и такая формализация ограничена и не позволяет, например, отличить неполноту сведений от их противоречивости. В обоих случаях истинность представляется числом 0.5 (всюду далее пользуемся отрезком [0, 1]), что обусловлено известным соотношением:

• (1)                                  H a H + I - a\\ = 1,

где a - некоторое суждение, ||^|| - его истинность, « - » - символ отрицания.

Та же ситуация и при использовании теории вероятности - ещё одного популярного способа формализации правдоподобных рассуждений [8, 9].

Несколько лучше обстоят дела, когда точка заменяется отрезком [10] или строгое равенство (1) неравенством:

\\a\\ + I-a\\ < 1, как в теории свидетельств Г. Шафера [11].

В работах [12, 13], благодаря использованию теории логик с векторной семантикой, истинность представлена вектором с произвольным (в общем случае) числом компонентов: \\ a \\ = { a 1 ; a ²;...; а^п > , a ' е [0, 1]. Значение каждого компонента определяется своим комплексом свидетельств (истинность в этом смысле здесь конструктивна). Позиции компонентов в векторе называются аспектами истинности, а их значения - значениями этих аспектов. Главная особенность таких логик - в полном снятии требований непротиворечивости и исключенного n -го: компоненты принимают значения независимо друг от друга, и сколько бы ни было аспектов, всегда можно предполагать наличие ( n + 1)-го, который проецируется в начало координат.

Наиболее изученным подклассом данных логик стала V ^гр-логика, в которой вектор истинности произвольного суждения a имеет два компонента: { a + ; a" ) . Значение первого компонента ( Истина ) - определяется свидетельствами подтверждающими, а второго ( Ложь ) -опровергающими a [12]. Именно этот вид логик предлагается использовать для верификации знаниевых моделей.

• 1    Логики с векторной семантикой как основа верификации

В логиках с векторными семантиками отсутствие сведений об изучаемых объектах формализуется вектором ( 0;...; 0 ) , а противоречие есть ситуация, когда компоненты логически исключают друг друга и при этом хотя бы два из них отличны от нуля. Каждый компонент формируется свидетельствами в его пользу. Недоверие к источникам, их ненадёжность приводят к значениям компонентов меньше единицы. Единица означает абсолютное доверие. С абсолютным доверием можно отнестись, в том числе, и к противоречащим друг другу источникам, что порождает вектор вида ( 1;...; 1 ) . То есть источник противоречия видится в разноречивости свидетельств.

В V ^TF-логиках предельные случаи выражаются векторами ( 0; 0 ) и ( 1; 1 ) . В [14] представлен интервальный вариант таких логик, когда значения компонентов являются подынтервалами отрезка [0, 1]. Компоненты в векторе делятся на позитивные и негативные . В частности, для V ^TF аспект Истина позитивный, аспект Ложь - негативный. Рост позитивного аспекта означает рост уверенности суждения реальности, рост негативного - её снижение.

Верификация означает организацию логического вывода, выявляющего ситуации, близкие к неопределённости ( 0;...; 0 ) или полному противоречию ( 1;...; 1 ) при тех или иных сочетаниях истинности входных фактов. Самое полезное здесь - это способность таких логик работать с ситуациями, близкими к неопределённости или полному противоречию, так же естественно, как со строгой истиной или строгой ложью. Под последними понимаются суждения, в которых все позитивные компоненты равны единице, а все негативные - нулю: строгая истина ( 1; 0 ) и строгая ложь ( 0; 1 ) .

Вывод в подобных логиках носит присоединённый характер, когда каждый шаг вывода сопровождается расчётом истинности заключения на основе истинности посылок [8, 15] и осуществляется на основе правила modus ponens с шагом в виде [12]:

• (2)                                    a , a ^ b ^ b : || b || = || a & i |Н| — avi ||,

где ||...|| - истинность суждения, через двоеточие указана схема расчёта истинности заключения на основе истинности посылок, i = a ^ b - импликация «если a , то b », «&» - конъюнкция (01-композиция), « v » - дизъюнкция (10-композиция); знак « ^» отделяет посылки от заключения, знак « ^ » использован для обозначения диапазона векторов истинности:

• (3)                                      || b || = ( [ a + • i ⁺, a ^-® i ⁺]; [ a + • i - , a ^-® i - ] ) .

Здесь для V ^TF-логик истинность конъюнкции и дизъюнкции (точнее, первых форм конъюнкции и дизъюнкции, которые в случае строгой истины и строгой лжи совпадают с конъюнкцией и дизъюнкцией в обычном смысле [12]) определяются как

|| a &b || = (a+• b+; a-® b-), || a vb || = (a+® b+; a-• b-), где • - триангулированная норма (t-норма), а ® - триангулированная ко-норма (s-норма) в инфиксной записи. Данные нормы определяются аксиомами [16, 17] (x, у е [0, 1]):

• 1)    x • у = у • x ;

• 2)    x•(у • z ) = ( у • x ) • z ;

• 3)    x • у 1 <  x • у ₂ если и только если у 1 < у ₂;

• 4)    x • I = x .

Аналогично:

• 1)    x ® у = у ® x ;

• 2)    x ® ( у ® z ) = (у ® x ) ® z ;

• 3)    x ® у 1 <  x ® у ₂ если и только если у 1 < у ₂;

• 4)    x ® 0 = x .

Для перехода от V ^TF к классической логике при строго истинных и строго ложных суждениях от них дополнительно требуется выполнимость свойств [12]:

• 1)    x * у = 1 - (1 - x ) Ф (1 - у );

• 2)    x Ф у = 1 - (1 - x ) * (1 - у ).

Из аксиом вытекает, в частности, что:

• (4)                             x • О = 0 и x Ф 1 = 1.

Известными примерами норм выступают x * у = xy и x Ф у = x + у - xy , а также x * у = min ( x , у ) и x Ф у = max ( x , у ) [17, 18].

В случае логик с произвольным числом компонентов t -норма для первой формы конъюнкции используется для позитивных, 5 -норма - для негативных компонентов. Для первой формы дизъюнкции - наоборот [13].

Поскольку для верификации, как правило, достаточно пользоваться категориями Истины и Лжи , далее применяются только V ^TF-логики.

В антецедентах больших посылок естественно-языковые связки И, ИЛИ формализуются, соответственно, первыми формами конъюнкции и дизъюнкции, а связка НЕ - отрицанием в форме перестановки: || — а || = ( a - а ⁺ ) .

• 2    Логический вывод и верификация

В качестве основы верификации принят логический вывод в V ^-логиках.

Если обе посылки строго истинны или близки к этому, то позитивный компонент близок к 1, негативный к 0. Согласно (2), (3) это условие формирует множество значений вектора истинности в прямоугольнике [ а + • i ⁺, а ^-Ф i ⁺] х [ а + • i”,а ^-Ф i ^- ], который при стремлении истинности посылок к ( 1; 0 ) (строгая истинность) стягивается в точку [1, 1] х [0, 0]. То есть истинные посылки влекут истинное заключение. Если БЗ не содержит внутренних дефектов, эта ситуация должна наблюдаться для любых допустимых значений истинности входных данных.

Ситуация меняется, когда знаниевая модель содержит артефакты. В данном случае это означает попадание на вход логического вывода (2) ложных, неопределённых или противоречивых утверждений. Возможны следующие варианты ситуации.

• I.    Одна из посылок ложная или строго ложная: ( 0; 1 ) . При строго ложной малой посылке согласно (2) и (3) получаем: || b || = ( [0 * i ⁺, 1 Ф i ⁺]; [0 * i , 1 Ф i | ) = ( [0, 1]; [0, 1] ) .

Областью возможных значений вектора истинности заключения становится весь квадрат [0,1] х [0,1], что делает значение || b || максимально размытым и неточным. В этом смысле энтропия истинности здесь максимальна.

При строго ложной большой посылке значение истинности заключения попадает в область, близкую строгой лжи: || b || = ( [ а ⁺ * 0, а ^-Ф 0]; [ а ⁺ * 1, а ^-Ф 1] ) = ( [0, а - ]; [ а ⁺, 1] ) .

Таким образом, если ложность малой посылки делает истинность заключения неизвестной, ложность большой порождает ложь в заключении.

• II.    Одна из посылок неопределённа: ( 0; 0 ) . Также рассмотрим неопределённость отдельно малой и большой посылок. Для малой посылки получается:

|| b || = ( [0 * i ⁺, 0 Ф i + ]; [0 * i - 0 Ф i - ] ) = ( [0, i + ]; [0, i - ] ) .

Неопределённость малой посылки помещает вектор истинности заключения в область [0, i ⁺] х [0, i ^- ]. Размер и границы этой области задаются вектором || i ||.

При неопределённости в импликации получаем:

|| b || = ( [ а ⁺ * 0, а ^-Ф 0]; [ а ⁺ * 0, а ^-Ф 0] ) = ( [0, а - ]; [0, а - ] ) .

Иначе говоря, областью истинности вектора || b || оказывается квадрат со сторонами [0, a ^- ] х [0, a ^- ]. Если малая посылка строго истинная или близка к таковой, неопределённость большой посылки порождает неопределённость заключения (вектор || b || расположен около точки ( 0; 0». Если же она строго ложная, приходим к уже известному квадрату [0, 1] х [0, 1] (рисунки 1 и 2).

Неопределённость и малой, и большой посылок приводит к неопределённости в заключении . При этом при высокой степени правдоподобия малой посылки неопределённость, порождаемая большой посылкой, существенна.

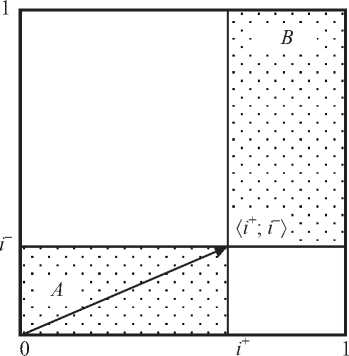
Рисунок 1 - Области неопределённости ( A ) и противоречивости ( B ) при неопределённости и противоречивости малой посылки

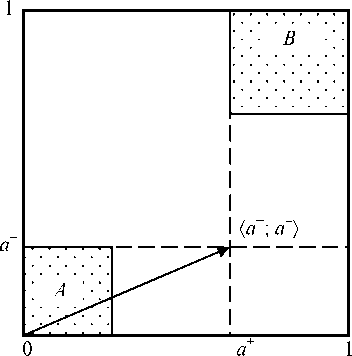
Рисунок 2 - Области неопределённости ( A ) и противоречивости ( B ) при неопределённости и противоречивости большой посылки

• III.    Одна из посылок противоречива: ( 1; 1 ) . Если это малая посылка, то:

|| b || = ( [1 • i ⁺, 1 ® i ⁺]; [1 • i\ 1 ® i D = ( [ i ⁺,1]; [ i ^- ,1] ) .

Это область [ i ⁺, 1] х [ i ^- , 1] - относительно близкая к ( 1; 1 > (точнее, к [1, 1] х [0, 1]).

Если противоречива посылка большая: || b || = ( [ а ⁺, 1]; [ а ⁺, 1] ) .

То есть при достаточно достоверной малой посылке вновь получается область, близкая к ( 1; 1 > (рисунки 1 и 2). Если же она строго ложная или близкая к таковой - весь или почти весь квадрат [0, 1] х [0, 1].

Таким образом, противоречивость как малой, так и большой посылок приводит к противоречивости заключения .

Для количественного определения величины определённости, противоречивости, неопределённости, строгости и т.д. разработаны соответствующие числовые меры [12, 18].

Мера определённости ( определённость ): Д )( b ) = b ⁺ ® b ^- , где Д )( b ) е [0, 1]. Данный показатель характеризует степень «удалённости» || b || от ( 0; 0 ) . Он равен 0, если || b || = ( 0; 0 ) и равен 1, когда хотя бы один из компонентов вектора истинности есть 1.

Мера противоречия ( противоречивость ): ц _п (b ) = b ⁺ • b ^- , где ц _п (b ) е [0, 1]. Данный показатель характеризует близость b к ( 1; 1 ) . Он равен единице для ( 1; 1 ) и нулю, когда хотя бы один из компонентов вектора || b || есть ноль.

Мера строгости ( строгость ): ц с (b ) = Д )( b ) - ц _п (b ) = b ⁺ ® b ^- - b + • b ^- , где ц с (b ) е [0, 1]. Назначение этого показателя - оценивать, насколько || b || близко к ( 1; 0 ) или ( 0; 1 ) . Он достигает максимума 1, когда || b || = ( 1; 0 ) , или || b || = ( 0; 1 ) и минимума 0, когда || b || = ( 0; 0 ) , или || b || = ( 1; 1 ) .

Мера достоверности ( достоверность ): д _д ( b ) = b ⁺ - b ”, где д _д ( b ) е [-1, 1]. Показатель принимает значение 1 для строго истинных и - 1 для строго ложных суждений. Содержательно данный показатель близок к предыдущему, однако позволяет определить не просто близость || b || к ( 1; 0 ) или ( 0; 1 ) , но уточнить конкретный случай. На его основе можно сформировать ещё один вариант меры строгости: Д ;( b ) = | д д ( b )| = | b ⁺ - b ^- |.

Мера избыточности ( избыточность ): д _и ( b ) = b ⁺ + b - - 1. Показатель равен - 1 для неопределённости и 1 для полного противоречия. Это - своеобразный аналог показателя достоверности для оси «Неопределённость-Противоречие». Равенство 0 здесь означает выполнение соотношения b ^- = 1 - b ⁺, характерного для нечётких логик. Позитивные и негативные свидетельства в этом случае «сбалансированы». Нулевой баланс существует, в частности, когда отсутствие свидетельств «за» рассматривается как свидетельство «против», а отсутствие свидетельств «против» - как свидетельство «за». Это типично для нечётких логик.

Абсолютное значение избыточности рассматривается как мера логического дисбаланса суждения b (степень нарушения соотношения «логического баланса» b ⁺ + b ^- = 1):

д _Дис ( b ) = | b ⁺ + b ^- - 1|.

Показатель равен 0 для классической и нечёткой логик и стремится к единице, если суждение становится в значительной степени противоречивым или неопределённым.

При интервальном представлении вектора истинности показатели можно рассчитывать относительно центра прямоугольной фигуры как репрезентативного значения вектора || b ||. Причём для прямоугольника [ b ⁺ 1 ; b ⁺₂] х [ b ”1; b ^- ₂] можно ввести меру точности определения вектора согласно формуле:

N b ) = 1 - sqrt ([( b ⁺ 2 - b ⁺1 )² + ( b"г - b ^- 1 )²] / 2).

Когда область возможных значений вектора охватывает весь квадрат [0, 1] х [0, 1], эта мера равна нулю, когда стягивается в точку - единице. Величину:

4b ) = sqrt ([( b ⁺ 2 - b ⁺1 )² + ( b"г - b ^- 1 )²] / 2) можно рассматривать как своеобразный показатель энтропии истинности суждения b при интервальных значениях || b ||.

• 3    Методы верификации

Главное предположение - артефакты знаниевой модели есть результат её структуры, но не истинностных значений посылок; последствия артефактов проявятся при любых допустимых значениях истинности стартовых (входных) посылок, вовлекших артефакт в процесс логического вывода.

К последствиям артефактов относятся:

• I.    Неучастие единицы знаний в выводе при всех (допустимых) значениях истинности входных посылок.

• II.    Неопределённость заключения при некоторых (допустимых) значениях истинности входных посылок и наличие нигде не используемых терминов.

• III.    Противоречивость заключения при некоторых (допустимых) значениях истинности входных посылок.

Верифицировать в данном случае - это установить, что при допустимых значениях истинности входных посылок ситуации I-III не возникают.

В разделе 2 показано, что ложь, неопределённость и противоречие импликаций порождают аналогичные последствия в заключениях. Можно сразу исключить такие единицы зна- ний из обсуждения, тем более, что разработчики БЗ вряд ли станут их вводить1. Источником проблем будут конфликты единиц знаний и входных данных, приводящие к ложным, неопределённым, противоречивым или близким к этому заключениям на разных этапах вывода. Вопрос верификации есть вопрос организации вывода, который вскроет артефакты.

Если активизировать только продукции со строго истинным антецедентом, «плохие» продукции никогда не активизируются. Следовательно, соответствующие артефакты можно выявить простым подсчётом числа активаций продукций при переборе всех допустимых значений входных посылок. Продукции с нулевым числом срабатываний могут быть исключены из БЗ как дефектные либо избыточные.

Появление неопределённости 〈 0; 0 〉 в ходе вывода в первую очередь связывается с обрывом цепочек рассуждений. В условиях, когда на вход подаются только строго истинные или строго ложные суждения, обрыв возникает исключительно тогда, когда антецедент правила строго ложен. Это возвращает к предыдущему случаю. Соответствующая продукция не срабатывает, и её консеквент остаётся неопределённым. Вывод при этом можно не останавливать, на выходе получается та же неопределённость, после чего обратной трассировкой можно выяснить источник проблемы. Однако представляется, что эффективнее будет его остановить по условию низкого значения меры определённости µ о ( b ). Если такое же требование ввести и для достоверности – останов при малом значении меры достоверности µ д ( b ), – то оба случая укладываются в следующую схему:

• 1)    объявить все продукции строго истинными (запомнив, при необходимости, первоначальные значения их истинности, выставленные экспертами);

• 2)    выставить значения истинности входных посылок в одну из допустимых комбинаций 〈 1; 0 〉 или 〈 0; 1 〉 , а истинность промежуточных и терминальных заключений в 〈 0; 0 〉 ;

• 3)    возвращаясь к шагу 2, выполнить прямой логический вывод, перебирая все допустимые значения истинности входных посылок в виде комбинаций строгой истины и строгой лжи и подсчитывая число срабатываний каждой продукции;

• 4)    при обнаружении продукций с нулевым числом срабатываний переработать их или удалить из БЗ;

• 5)    вернуть исходные значения истинности оставшихся продукций;

• 6)    КОНЕЦ.

Сложнее ситуация с противоречиями. Выявление противоречий опирается на отмеченное в разделе 2 свойство вывода в V TF -логиках: перенос противоречия из посылки в заключение. Это означает, что если в ходе рассуждений истинность некоторого промежуточного заключения примет противоречивое значение, эта особенность пройдёт через весь последующий вывод и проявится в истинности терминальных утверждений – гипотез. Появление этих особенностей – сигнал о неблагополучии в БЗ. Обратной трассировкой вывода можно найти и его источник – артефакт. Алгоритм может выглядеть так:

• 1)    объявить продукции строго истинными (запомнив значения истинности, выставленные экспертами);

• 2)    выставить значения истинности входных посылок в одну из допустимых комбинаций 〈 1; 0 〉 или 〈 0; 1 〉 , а истинность промежуточных и терминальных заключений (гипотез) в 〈 0; 0 〉 ;

• 3)    выполнить прямой логический вывод, получив истинность заключений (гипотез);

• 4)    проверить истинность заключений на допустимость;

• 5)    если заключение недопустимо (вектор истинности равен 〈 1; 1 〉 ), то:

• 5.1)    выполнить обратную трассировку вывода для выяснения источника проблемы -артефакта БЗ;

• 5.2)    устранить артефакт (или внести его в соответствующий список);

• 5.3)    вернуться к шагу 2;

1 На практике подобные единицы знаний могут быть введены в БЗ как непреднамеренно, так и преднамеренно. Прим. ред.

• 6)    если не все возможные входные значения посылок проверены, то вернуться к шагу 2;

• 7)    вернуть исходные значения истинности продукций;

• 8)    КОНЕЦ.

Противоречивость того или другого утверждения формируется, когда, например, две цепочки вывода приходят к двум взаимоисключающим результатам: b и — b. Противоречие ( 1; 1 ) в этом случае - результат обязательной для такого вывода процедуры объединения свидетельств. Нигде не используемые термины обнаруживаются отсутствием привязки к продукциям. Данное обстоятельство вскрывается также обратной трассировкой от гипотез к входным фактам. Не используемые термины не попадают ни в одну из потенциальных цепочек вывода.

• 4 Объединение свидетельств как часть логического вывода

Объединение свидетельств - важнейшая составляющая присоединённого правдоподобного вывода [19]. Его цель - объединение истинностных значений суждения, полученного по разным цепочкам вывода. В том числе, когда по одной из цепочек получено заключение b , а по другой — b (противоречие). Рассматриваются понятия 10-, 01-, 11- и 00-композиций в V ^TF-логиках.

10-композицией называется суждение, образованное из b 1 и b 2 с вектором истинности ( b 1 ⁺ ® b ₂⁺; b /• b ₂ ⁺ ) . Своими свойствами она повторяет классическую дизъюнкцию и потому называется также первой формой дизъюнкции: || b 1 v b ₂|| = ( b 1 ⁺ ® b ₂⁺; b /• b ₂ ⁺ ) .

01-композицией называется суждение, образованное из b 1 и b 2 с вектором истинности ( b /• b ₂⁺; b 1 ⁺ ® b ₂ ⁺ ) . Она соответствует классической конъюнкции и названа первой формой конъюнкции: || b 1 & b ₂|| = ( b /• b ₂⁺; b 1 ⁺ ® b ₂ ⁺ ) .

11-композицией называется суждение, образованное из b 1 и b 2 с вектором истинности ( b 1 ⁺ ® b ₂⁺; b 1 ⁺ ® b ₂ ⁺ ) . Аналогов в классической и нечёткой логике эта связка не имеет. Она названа второй формой дизъюнкции : || b 1 v ₂ b ₂|| = ( b 1 ⁺ ® b ₂⁺; b 1 ⁺ ® b ₂ ⁺ ) .

00-композицией называется суждение, образованное из b 1 и b ₂ с вектором истинности ( b /• b ₂⁺; b /• b ₂ ⁺ ) . В классической и нечёткой логике данная связка тоже не имеет аналогов. Она названа второй формой конъюнкции : || b 1 &₂ b ₂|| = ( b /• b ₂⁺; b /• b ₂ ⁺ ) .

Если первые формы дизъюнкции и конъюнкции соответствуют связкам ИЛИ и И в обычном смысле, то вторые формы - это связки ИЛИ и И в информационном смысле: они дают рост как позитивного, так и негативного компонентов для ИЛИ и некое минимальное гарантированное значение этих компонентов для И.

В случае п- мерного вектора истинности вторая форма дизъюнкции - это 5 -норма ® для всех компонентов вектора, в случае второй формы конъюнкции - t -норма • также для всех компонентов вектора истинности. С учётом этих особенностей V ^TF-логики имеют богатый арсенал способов объединения. В частности, рассматриваются следующие стратегии [20]:

• 1)    объединение по схеме 10/11 -композиции - стратегия нарастающего доверия . Векторы || b || и || — b || объединяются по-отдельности по правилу 10-композиции (дизъюнкции). После того, как объединены все свидетельства в пользу b и все свидетельства в пользу — b , векторы || b || и || — b || складываются в единый вектор по правилу 11-композиции. Доверие к b возрастает по мере получения утвердительных доказательств факта, доверие к — b - по

мере вывода его отрицаний. Наличие «сильных» доказательств того и другого ведёт к противоречию в b .

• 2)    объединение по схеме 01/00 -композиции – стратегия нарастания недоверия . Свидетельства в пользу b и свидетельства в пользу b объединяются по-отдельности на основе 01-композиции (конъюнкции). После объединения всех свидетельств оба результирующих вектора объединяются по правилу 00-композиции. В результате доверие и к b , и к b будет тем меньше, чем менее убедительны соответствующие свидетельства. Общий результат даёт гарантированный минимум доверия к факту и его отрицанию, определяемый худшими из подтверждающих и опровергающих свидетельств.

• 3)    объединение по схеме 11 -композиции – стратегия полного доверия . Доверяют «без разора» и подтверждающим, и опровергающим свидетельствам. Вариант стратегии нарастающего доверия, но здесь быстрее растёт степень противоречивости факта.

• 4)    объединение по схеме 00 -композиции – стратегия полного недоверия . Доверяют «худшим» из подтверждающих и опровергающих свидетельств. Вариант стратегии нарастающего недоверия, но здесь быстрее растёт степень неопределённости факта. В итоге это может привести к неопределённому 〈 0; 0 〉 восприятию факта: «не верю ни чему».

• 5)    объединение по схеме 10 -композиции – стратегия безудержного оптимизма . Всё решают свидетельства в пользу b .

• 6)    объединение по схеме 01 -композиции – стратегия безудержного пессимизма . Всё решают свидетельства в пользу b .

• 7)    объединение по правилу среднего (арифметического, геометрического и т.д.) – стратегия осторожной веры . Свидетельства «за» и «против» усредняются.

Для заявленной цели наиболее подходящими являются стратегии «нарастающего доверия» - 1 и «полного доверия» – 3. И тот и другой подходы при получении заключений b и b генерируют вектор истинности 〈 1; 1 〉 . Например, если по некоторой ветви вывода получено заключение b с истинностью || b || = 〈 1; 0 〉 , а по другой b также с истинностью || b || = 〈 1; 0 〉 , то объединение на основе 11-композиции даёт (с учётом, что || b || = 〈 b ^– ; b + 〉 ) полное противоречие: || b || = 〈 1 ⊕ 0; 0 ⊕ 1 〉 = 〈 1; 1 〉 .

Принимая во внимание свойство противоречия в посылке генерировать противоречие в заключении, следует сделать вывод, что противоречивым оказывается и терминальное утверждение – гипотеза. Это – сигнал о противоречии в БЗ, и необходимо обратиться к алгоритму, приведённому в разделе 3.

Заключение

В работе рассмотрены общие вопросы формализации поиска артефактов в продукционных БЗ на основе логик с векторной семантикой в варианте V TF -логики. Алгоритмизация рассматривается как организация прямого присоединенного логического вывода, вскрывающего артефакты БЗ. Рассмотрены три случая обнаружения артефактов БЗ.

• I.    Ложность антецедента какой-либо продукции при всех допустимых значениях истинности входных посылок, что приводит к обрыву цепочки вывода и неиспользованию соответствующей продукции.

• II.    Неопределённое значение истинности 〈 0; 0 〉 консеквента продукции при тех или иных допустимых значениях истинности входных посылок, что также влечёт неиспользованием продукции.

• III.    Появление противоречия в выводе в виде вектора истинности 〈 1; 1 〉 на одном из шагов рассуждений.

Первые два случая предложено обнаруживать подсчётом числа срабатываний каждой продукции. Продукция с нулевым количеством срабатываний является подозрительной на артефакт. Для выявления неактивных единиц знаний рекомендуется останавливать вывод не только по условию ложности, но и по условию неопределённости антецедента продукции, для чего использовать меры достоверности и определённости.

Третий случай выявляется выводом с проверкой истинности заключений - гипотез. Наличие заключения с истинностью 〈 1; 1 〉 (полное противоречие) сигнализирует о противоречии на одном из этапов рассуждений. Так как противоречие в посылках порождает противоречие в заключении, обратная трассировка вывода позволяет обнаружить момент и причину появления противоречия, указывая артефакт. Необходимым этапом такого вывода является объединение свидетельств с использованием 11-композиции (второй формы дизъюнкции).