Локализация пластического сдвига и механизмы разрушения при динамическом нагружении металлов

Локализация пластической деформации металлов, подвергнутых динамическому нагружению, является многофакторным процессом, зависящим от скорости и величины деформации, температуры, а также эволюции структуры материала. Так, в работе [1] показано, что одним из механизмов формирования полос пластического сдвига являются множественные многомасштабные неустойчивости в системе микросдвигов (дефектов мезоуровня), сопровождающиеся пластическими ротациями, изменением ориентации зерен в узких полосах сдвига. Исследованию данного явления посвящен цикл работ [1–17].

В настоящей работе изучается локализация пластического течения при динамическом нагружении металлов на основе развитой структурно-феноменологической модели твердых тел с дефектами [18, 19] и оригинальных экспериментов по регистрации in-situ кинетики и термодинамики развития неустойчивости пластического сдвига и структурных исследований. Скачкообразный переход к более упорядоченной дефектной структуре часто приводит к изменениям деформационных свойств, которые могут проявиться при динамическом нагружении в условиях чистого сдвига и при высокоскоростном соударении ударника с преградой (выбивание пробки) [20–28].

Динамическое нагружение металлических образцов осуществлялось по двум схемам: сжатие на установке Гопкинсона–Кольского образцов П-образной формы с концентратором напряжений (из сплава Д16) и выбивание пробки (в мишени из алюминиевого сплава А6061) разгоняемым ударником [21–23]. В качестве ударника при испытании образцов на пробивание использовался стержень из высокоуглеродистой стали диаметром 5 мм, длиной 50 мм и массой 7,4 г. Скорости соударения составляли 101–280 м/с.

Схемы экспериментов по реализации нагружения, близкого к чистому сдвигу, и по пробиванию металлических преград представлены на рисунке 1. Использование инфракрасной камеры CEDIP Silver 450M позволило проследить in-situ картину распределения температур вблизи зоны локализации деформации (Рис. 2).

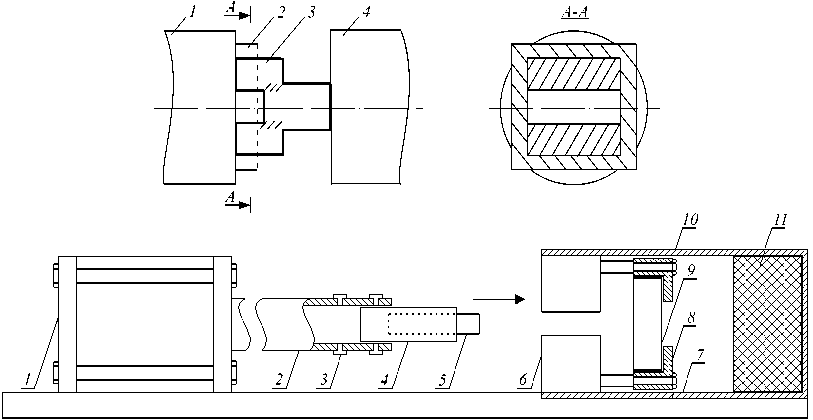
Рис. 1. Схемы экспериментов: ( а ) – нагружение металлических образцов в условиях, близких к чистому сдвигу: 1 – входной стержень, 2 – рамка-держатель, 3 – образец, 4 – выходной стержень; заштрихованные области находятся в состоянии близком к чистому сдвигу; ( б ) – испытание образцов на пробивание: 1 – камера высокого давления, 2 – ствол, 3 – фотодатчики, 4 – поддон, 5 – ударник, 6 – отсекатель, 7 – рама, 8 – устройство для крепления мишени, 9 – мишень, 10 – приёмная камера, 11 – улавливатель

а

б

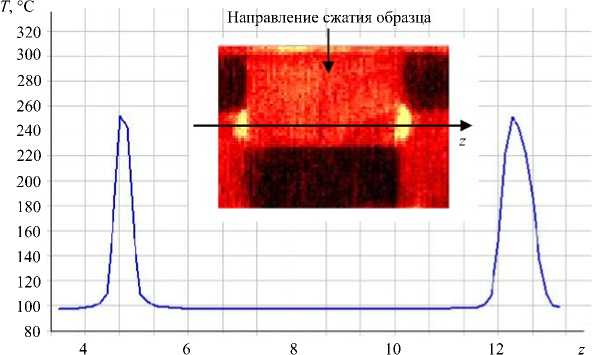
Рис. 2. Профиль температуры боковой поверхности плоского П-образного образца из сплава Д16, подвергнутого динамическому сжатию, с характерными зонами интенсивной сдвиговой деформации

Микроструктурные исследования слоев материала, расположенных вблизи зоны локализации деформации, показали существенное увеличение плотности дислокаций и формирование ячеистой дислокационной структуры как для случая динамического нагружения, так и для выбивания пробки (Рис. 3). Просвечивающая электронная микроскопия образцов проводилась в Институте физики металлов УрО РАН (г. Екатеринбург) с участием профессора И.Г. Бродовой и научного сотрудника А.Н. Петровой [21, 22]. Восстановленные величины сдвиговых деформаций по смещению линий течения, а также

950 нм

а

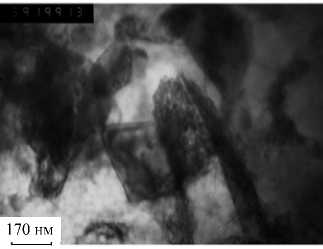
Рис. 3. Ячеистая дислокационная структура образцов в зонах локализации деформации при динамическом сжатии ( а ) и после выбивания пробки ( б )

результаты измерения микротвердости выявили расширение области деформированного материала по мере продвижения ударника в материале мишени.

При помощи сканирующей электронной микроскопии поверхностей разрушения, образующихся при выбивании пробки, обнаружился неоднородный характер распространения разрушения в материале мишени: так, в зоне, соответствующей сдвиговым механизмам деформирования материала и начальному формированию магистральной трещины, шероховатость поверхности разрушения оказалась относительно малой, с низкими значениями параметров масштабной инвариантности. В зоне, соответствующей финальному распространению магистральной трещины, рельеф поверхности разрушения стал более грубым, параметры масштабной инвариантности выросли.

Повышение твердости, характер расположения линий течения материала и их сгущение вблизи поверхности разрушения, а также результаты просвечивающей электронной микроскопии позволяют сделать вывод об интенсивных структурных изменениях, сопровождающих процессы локализации пластического течения при динамическом нагружении металлов.

3.    Моделирование процесса локализации пластического сдвига Vo Рис. 4. Плоский слой в условиях чистого сдвига описывалось следующими уравнениями [18, 24]:

Численное моделирование механизмов неустойчивости пластического сдвига и локализации пластической деформации (в квазиодномерной постановке) проводилось с учетом особенностей кинетики накопления микросдвигов в материале. Рассматривалось деформирование плоского слоя толщиной h в условиях чистого сдвига. Одна сторона слоя была жестко закреплена, на другой задавалась постоянная скорость v ₀ (Рис. 4).

Поведение материала плоского слоя с учетом кинетики накопления микросдвигов в материале дvx _ дт xz p д t " дz ’

T =/gp _/ ^L Lxz    4еxz   21 ~ , д t др = к е p - £ п д t     13   xz    13

д

^П = - ^A1 ^T xz exP ⁽ - Pa P ) + ^B1⁽ P - P b ) - ^D , д z

Использовались начальные и граничные условия:

^т xz ( ^{z ,0} ) = 0;      v x ^{( z} ,0) = 0;      v x (0, t ) = 0;      v x ⁽ h, t ) = v o ;

p ( z, 0) = p ₀ sin⁸( n z/h );

| p (0, t ) = | p ( h , t ) = 0. д z        д z

В выражениях (1)-(6) приняты обозначения: p — плотность материала слоя; v_x, — компонента вектора скорости; е p — компонента тензора пластических деформаций; т xz — компонента тензора напряжений; l ₁ , l ₂ , l ₃ — кинетические коэффициенты; A ₁ , B ₁ , p_a , p_b — параметры аппроксимации; p — компонента тензора плотности микросдвигов; D ₁ — параметр нелокальности

Неоднородное пластическое течение слоя и дальнейшая локализация пластической деформации инициировались начальным неоднородным распределением компоненты тензора плотности микросдвигов. Принималось условие аддитивности упругих ( е xz ) и пластических ( е p ) скоростей деформаций:

е

xz

=е e +е ^р xz xz

.

Поведение материала слоя описывалось уравнением:

дтхг  V 5 Vx

----= GI --- д t ( дг

—

I

p xz

где G — модуль сдвига. При численном решении системы уравнений (1)–(8) использовалась конечно- разностная схема второго порядка точности.

В процессе высокоскоростного деформирования в материале происходит структурно-кинетический переход по параметру плотности микросдвигов в локальной области, который характеризуется быстрым ростом параметра плотности микросдвигов (Рис. 5, а ). Это приводит к резкому — скачкообразному, изменению эффективных характеристик среды, в частности, к падению эффективной вязкости, и, как следствие, к быстрому росту скорости пластической деформации и релаксации напряжений и, следовательно, падению сопротивления сдвигу в этой области (Рис. 5, б ).

а

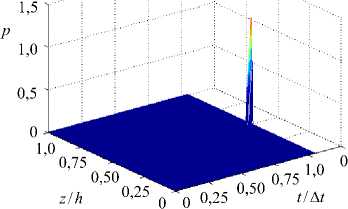
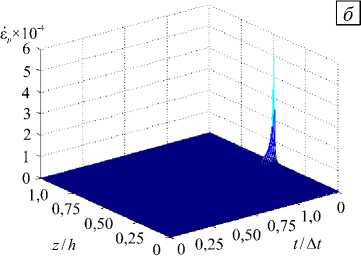
Рис. 5. Распределение компоненты тензора плотности микросдвигов ( а ) и скорости пластической деформации ( б ); Д t - характерное время

Таким образом, модель упруго-пластического поведения материала с учетом кинетики накопления микросдвигов описывает процессы неустойчивости пластического сдвига и локализации пластической деформации. Данные теоретических и экспериментальных исследований позволяют предположить, что один из механизмов неустойчивости пластического сдвига и локализации пластической деформации при динамическом нагружении обусловлен структурно-кинетическими переходами в ансамблях микросдвигов.

4.    Трехмерная математическая модель

Полная математическая постановка, описывающая деформирование и разрушение твердых тел с мезоскопическими дефектами при динамических и квазистатических условиях нагружения, представлена в работах авторов [29–34] и в данной работе применена для трехмерного численного моделирования динамического нагружения металлов в условиях чистого сдвига. Система дифференциальных уравнений модели имеет вид

V- ст = р и, (9) 1 dP =— v-V, р dt (10) 8 = 8 e + p + 8 p , (11) CT = CTs +стd , (12) P = P s + P d , (13) CT = XIj(8e) + 2G8e, (14) ст = A18 p — A2 p, (15) 8F —= Aзр — A 2 8 p, др (16) дF _ Ж A4^, до (17) A22 > 0,   Ai > 0, i = 1,4 (18) и включает: уравнения движения (9); уравнения неразрывности (10); гипотезы аддитивности упругой, пластической и структурной деформаций (11); представление напряжения в виде разложения на шаровую и девиаторную части (12); аналогичное разложение для деформации, обусловленной дефектами (13); закон Гука в скоростной форме (14); определяющие соотношения для макроскопических переменных, характеризующие неупругое поведение среды (15)–(17); ограничения на кинетические коэффициенты (квазиравновесный подход Онсагера) (18).

В выражениях (9)–(18) используются обозначения: σ — напряжение, при этом σ _s и σ _d — его шаровая и девиаторная составляющие; u — перемещение; ρ — плотность; V — скорость; ε — полная деформация, при этом ε ^e и ε ^p — ее упругая и пластическая составляющие; p — тензор плотности дефектов, физический смысл которого есть деформация, обусловленная дефектами, где p _s и p _d — его шаровая и девиаторная части; I1( e e ) — первый инвариант скорости упругой деформации; X и G — первый и второй параметр Ламе; F — свободная энергия Гельмгольца (термодинамический потенциал); δ — параметр структурного скейлинга; A_i — кинетические коэффициенты, которые в общем случае зависят от инвариантов p [18, 19]. Переменные p и δ имеют смысл независимых термодинамических переменных среды с дефектами (аналогичных параметрам порядка в теории фазовых переходов).

Разрушение материала представляется как процесс накопления повреждений (микросдвигов, микротрещин), а критерием разрушения является условие достижения инвариантами введенного тензора плотности дефектов своих критических значений.

Трехмерная математическая модель (9)–(18) реализована в пакете прикладных программ Abaqus/Explicit в виде отдельного программного модуля, задающего свойства материала. С ее использованием рассмотрено динамическое нагружение П - образного образца в условиях чистого сдвига (Рис. 6). На торце образца, граничащего с входным стержнем, задавались граничные условия в виде известного импульса напряжений, а на противоположном торце — нулевые перемещения, Остальные поверхности образца считались свободными. Граничные условия представлялись соотношениями:

Γf : σ⋅n=f(t), Γ0 :σ ⋅n =0, Г u : u = u, (t), где Γ f — граница образца, на которой прикладывался входной импульс напряжений, Γ0 — свободная поверхность образца, Γu — граница образца, на которой были известны перемещения. Начальные условия по всем переменным модели выбирались однородными.

Результаты численного моделирования динамического нагружения П - образного образца в различные моменты времени представлены на рисунке 6. Из полученных распределений поврежденности —

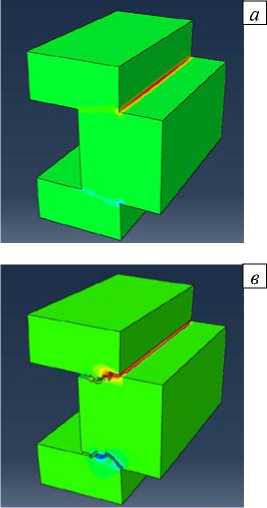
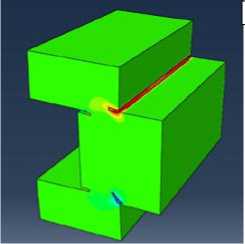
б

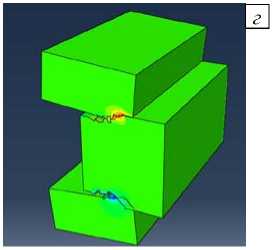
Рис. 6. Результаты численного моделирования: распределение поврежденности и геометрия трещины в различные моменты времени t , мкс: 8 ( а ); 16 ( б ); 20 ( в ); 50 ( г )

р=хЮ

1 О

-1

-2

-3

-4

-5

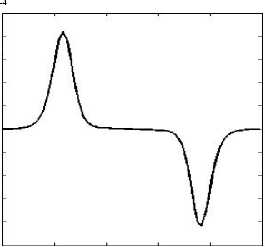
О 0,2     0,4    0,6     0,8 zih

Рис. 7. Зависимость деформации сдвига, обусловленной дефектами, в момент времени t = 10 мкс

деформации, обусловленной дефектами, можно сделать заключение, что зарождение и рост дефектов сопровождаются пластическими деформациями в зонах, где реализуется состояние чистого сдвига, приводящими к повышению температуры этих зон, которая и регистрируется методами инфракрасного сканирования температурных полей (Рис. 2).

На рисунке 7 представлено распределение вдоль вертикальной оси z деформации p_xz , обусловленной дефектами, в центре П - образного образца в момент времени нагружения 10 мкс. Показанная зависимость отражает интенсивный рост дефектов в зонах сдвига, который сопровождается пластической деформацией и, как следствие, приводит к нагреванию материала (см. экспериментально полученную зависимость температуры на рисунке 2).

5.    Обсуждение результатов

Проведенные микроструктурные исследования позволили восстановить картину деформационных процессов, протекающих при динамическом нагружении мишеней из алюминиевого сплава А6061 и сплава Д16. Стадийность процесса пробивания отражается в особенностях формирования рельефа поверхности разрушения и прилегающих к ней внутренних слоев материала. Показано существенное увеличение плотности дислокаций и формирование ячеистой дислокационной структуры в областях локализации пластического течения как при динамическом нагружении образцов, так и при нагружении мишеней, сопровождающемся инициированием «пробки».

Используемая математическая модель позволила описать процесс деформирования и разрушения металлов в условиях чистого сдвига. Проведенные на ее основе расчеты подтвердили, что выбранные два параметра порядка (обусловленная дефектами деформация и структурный параметр) описывают эволюцию дефектной структуры материала в условиях динамического нагружения. Предложенный вид критерия разрушения определяет условие, при котором наступает разрушение, что позволяет установить место и момент наискорейшего зарождения и роста дефектов, что в дальнейшем приводит к образованию макроскопической трещины и окончательному разрушению образца.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0068 от 23.05.2013 г. в составе мероприятий по реализации Постановления Правительства РФ № 218).