Локально-двумерные схемы расщепления для параллельного решения трехмерной задачи транспорта взвешенного вещества
Автор: Сухинов Александр Иванович, Чистяков Александр Евгеньевич, Сидорякина Валентина Владимировна, Проценко Софья Владимировна, Атаян Ася Михайловна
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Моделирование, информатика и управление
Статья в выпуске: 2 т.24, 2021 года.
Бесплатный доступ
Рассматривается 3D-модель транспорта взвесей в прибрежных морских системах, учитывающая множество факторов, среди которых гидравлическая крупность или скорость осаждения частиц, распространение взвеси, оседание, интенсивность распределения источников взвешенного вещества и др. Разностные операторы диффузионного переноса в горизонтальных и вертикальном направлениях для данной задачи обладают существенно различными характерными пространственно-временными масштабами процессов, а также спектрами. При типичной дискретизации, применительно к мелководным системам Юга России (Азовское море, Цимлянское водохранилище), шаги по горизонтальным направлениям составляют 200-1000 м, коэффициенты турбулентного обмена (турбулентной диффузии) (103-104)м2/с; по вертикальному направлению - шаги 0,1 м-1 м, а коэффициенты микротурбулентного обмена по вертикали - (0,1-1)м2/с. Если ориентироваться на использование явных локально-двумерных - локально-одномерных схем расщепления, то допустимые значения шага по времени для двумерной задачи составят порядка 10-100 с, а для одномерной задачи по вертикальному направлению - 0,1-1 с. Сказанное мотивирует к построению аддитивной локально-двумерной - локально-одномерной схемы расщепления по геометрическим направлениям. В работе приведено описание параллельного алгоритма, использующего для аппроксимации двумерной задачи диффузии-конвекции по горизонтальным направлениям и одномерной задачи диффузии-конвекции по вертикальному направлению как явными, так и неявными схемами. Двумерная неявная задача диффузии-конвекции по горизонтальным направлениям численно решается адаптивным попеременно-треугольным методом. Численная реализация одномерной задачи диффузии-конвекции по вертикальному направлению осуществляется последовательным методом прогонки для серии независимых на данном слое одномерных трехточечных задач по верти кальному направлению. Для повышения эффективности параллельных расчетов также выполнена декомпозиция расчетной пространственной сетки и всех сеточных данных по одному или двум пространственным направлениям - в горизонтальных направлениях. Проведено сравнение полученных алгоритмов с учетом допустимых величин шагов по времени и реальных временных затрат на выполнение вычислений и обменов информацией на каждом временном слое.
Транспорт взвешенного вещества, численные методы, схемы расщепления, локально-двумерные схемы расщепления, параллельные алгоритмы
Короткий адрес: https://sciup.org/149138014
IDR: 149138014 | УДК: 519.6 | DOI: 10.15688/mpcm.jvolsu.2021.2.4
Текст научной статьи Локально-двумерные схемы расщепления для параллельного решения трехмерной задачи транспорта взвешенного вещества
DOI:
ул. Инициативная, 48, 347936 г. Таганрог, Российская Федерация
В статье рассматривается 3D-модель диффузии-конвекции-осаждения взвеси в водной среде и ее параллельная численная реализация на основе явных и неявных схем, а также расщепления по геометрическим направлениям с учетом особенностей прибрежной системы.
Реальная трехмерная турбулентность в прибрежных системах обладает рядом специфических особенностей, описанных, например, в работах [4; 9; 12]. Строго говоря, она может считаться локально-однородной и изотропной лишь в масштабах, значительно меньших глубины акватории, так как стратификацию воды хорошо перемешанного мелкого водоема ограничивает максимальный вертикальный размер турбулентных вихрей. Считается, что по последней причине процесс турбулентного перемешивания можно разделить на горизонтальный турбулентный обмен и вертикальную турбулентную диффузию. Операторы конвективного и диффузионного переноса в горизонтальных и вертикальном направлениях для задач транспорта взвеси обладают существенно различными физическими и спектральными свойствами [7; 11; 18]. В связи со сказанным, для построения экономичных алгоритмов оперативного прогноза распространения взвеси (загрязнения водоема) целесообразно применять локально-двумерные схемы (ЛДС) расщепления [1; 16]. Ранее было показано для пространственно-трехмерных начально-краевых задач для уравнений параболического типа, что применение ЛДС позволяет получать малозатратные по количеству арифметических операций алгоритмы решения параболических сеточных уравнений, которые являются экономичными по числу операций и времени, необходимого для осуществления обменов между процессорами [17].
1. Непрерывная 3D-модель диффузии-конвекции-осаждения взвесей
Будем использовать прямоугольную декартову систему координат Oxyz , где ось Озе проходит по поверхности невозмущенной водной поверхности и направлена в сторону моря. Пусть h = Н + п — общая глубина акватории, [м]; Н — глубина при невозмущенной поверхности водоема, [м]; η — возвышение свободной поверхности относительно геоида, [м].
В модели осуществим переход от z -координатной системы к 0 -координатной системе, для которой используем декартову систему координат в горизонтальной плоскости, а в качестве вертикальной переменной — безразмерную переменную 0 , 0 G [0; 1] .
В θ -координатной системе водный столб разделен на одинаковое количество слоев в каждой точке независимо от глубины, поэтому при использовании «новой» координатной системы решаются некоторые проблемы, связанные с добавлением и вычитанием слоев.
При переходе к θ -координатной системе используем формулу:
0 = а
(а - 6)(z - п )
h
Х 0 = е, у 0 = у,
где 0 = а = 0 на свободной поверхности водоема (верхняя граница), 0 = b = 0 на дне (см. рис. 1).
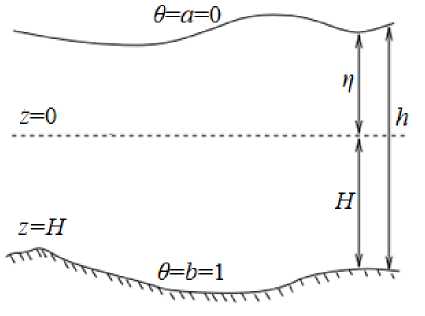
Рис. 1. θ -координатная система
Далее вместо выражений (1) будем использовать соотношения
0 = ^ - , X 0 = X, У 0 = у.
h
Пусть в водном объеме V = { 0 < х < L x , 0 < у < L y , 0 < 0 < 1 } находятся частицы взвеси, которые в точке (х, у, 0 ) и в момент времени t имеют концентрацию с = с(х,у, 0 ,t) , [мг/л]; t — временная переменная, t Е [0; Т] [сек].
Уравнение, описывающее поведение частиц, будет выглядеть следующим образом [6; 13]:
Эс д(ис) д(хс) а — b д ((w + W g ) с)
дt Эх ду h д 0
= ^ ( эу +й ) + (^ У(* д^ У + f. (3) дх 2 ду2 / \ h ) д 0 д 0 /
Здесь и , х , w — компоненты вектора U скорости движения жидкости, [м/с]; w g — гидравлическая крупность или скорость осаждения частиц, [м/с]; µ , ν — коэффициенты горизонтальной и вертикальной диффузии частиц, [м 2 /с]; F = F(х,у, 0 ,t) — функция, описывающая интенсивность распределения источников взвешенного вещества.
В совокупности с граничными условиями для функции концентрации частиц решение уравнения (3) позволяет определять потоки взвешенного вещества как по направлению к берегу, так и вдоль берега.
В качестве водного объема V рассматриваем трехмерную цилиндрическую область, верхнее основание которой лежит на свободной поверхности, а нижнее основание является частью донной поверхности. Отметим, что постоянная высота области V обусловлена переходом от координаты х по вертикали к координате 0 , 0 Е [0; 1] . Пусть Г = S U S tOp U S bottom — граница области V ; S — боковая граничная поверхность; S tOp , S bottom — части свободной поверхности и поверхности дна соответственно. Боковая поверхность S области V образуется в результате движения образующей по замкнутой линии, являющейся контуром аппроксимирующим береговую линию или « жидк у ю границу» расс ма триваемой области. Областью задания уравнения (3) считаем QT = V х { 0 < t <Т } , V = V U Г .
Добавим к уравнению (3) начальные и граничные условия (предполагая, что осаждение частиц на дно необратимо):
• начальные условия при t = 0
с^х/у, 0 , 0) = С о (а^у, 0 );
• граничные условия на боковой границе S в любой момент времени t дс дп
= 0, если ^U г ,п^ < 0,
дс дп
--г с, если ^U г ,п^ > 0,
где п — внешняя нормаль к границе области S , U г — вектор скорости движения жидкости на границе S , и г — проекция вектора скорости U г на направление нормали п на границе области S ;
-
• граничные условия
на поверхности
воды S top
дс д0
= 0;
-
• граничные условия
на дне S bottom
дс д0
W g
—с, ν
считая, что донная
поверхность не «сильно» искривлена.
В работах [3; 19] исследованы условия корректности задачи транспорта взвесей, в случае многокомпонентного гранулометрического состава частиц, а потому и задачи (3)–(8), как ее частного случая при условиях гладкости функции решения
с(х, у, 0 , t) G С 2 ( Q t ) П С(Q T ), grad с G С(Q T )
и необходимой гладкости границы области.
2. Метод построения аддитивной локально-двумерной схемы расщепления
Пусть функция с имеет ограниченные производные до четвертого порядка включительно по декартовым переменным х , у , 0 и до второго порядка включительно по временной переменной t , а функции F , F 1 , F 2 , для которых F = F 1 + F 2 , имеют ограниченные производные до второго порядка включительно по х , у , 0 и первого порядка по t в V .
Обозначим u 1 = u , и 2 = х , и 3 = w + w g .
Представим пространственно-трехмерные операторы конвективного переноса в форме:
д(и 1 с) д(u 2 с) а — b д(и 3 с)
дх ду
L c c =
h д 0
1 (9 (u i c) 9c\ 1 fd( u 2c) 9c\ 1 a - Ь(9и з 9c\
= 2 (.- + u i + 2 (■ ■ . + U 2 аЦ) + 2 TVSe+ u 3 35)- (9)
Dc = ц ( | 2 C + ^ ) + ( ^)2 £ (v Iе ) , (10)
\ dx 2 9y 2 / \ h ) d 0 \ 95)
где L c — линейный кососимметрический оператор.
Вводя следующие обозначения
L ci2 c = 1 ( ^+u i^ ) + 1 (/ ■ u,®)\ L c 3e = (^ + u| ) , (11)
2 \ dx ox) 2 \ dy dy ) 2h \ 9 0 90)
= ц ( ^ + ^) , D 3 c = (^) 2 1 (v f| ) , (12)
\ dx 2 dy2) \ h ) 90 \ 90)
для формул (9), (10) можем записать равенства
L c c = L ci2 c + L c3 c, Dc = D i2 c + D 3 c.
Используя введенные операторы L c c , Dc , уравнение (3) представим в виде
9c _ _ _
d^ = -L c c + Dc + F, t E [0; T ].
Будем для простоты рассматривать случай, когда функция источника действует на поверхности водоема, то есть выполнено условие F(x,y, 0 ,t) = F(x,y,t) .
На временном отрезке [0; T ] построим равномерную сетку шт с шагом т , то есть множество точек вида шт = {t n = п т , п = 0,N, N т = T } .
На введенной временной сетке ωτ заменим трехмерную задачу (13), (4)–(8) цепочкой двумерных-одномерных задач, связанных по начальным и финальным данным — значениям сеточных функций c (1) и c (2) :
= —Lc12c(1) + D12c(1) + F1) tn < t < tn+1, п = 0, N — 1,
c(i)(x,y, 0,0) = co(x,y, 0),
c(2)(x,y, 0,tn) = c(i)(x,y, 0,tn+i), п = 0,N - 1
и
= —Lc3c(2) + D3c(2) + F2, tn c(i)(x,y, 0,tn) = c(2)(x,y, 0,tn), п = 1,N - 1. Уравнения (14)–(16) и (17), (18) дополняются граничными условиями (5), (6) на боковой границе и граничными условиями (7), (8) на поверхностях воды и дна соответственно. Решением этой задачи является функция c(x, y, 0,tn) = c(2)(x,y, 0,t„), п = 1,N. В области V построим равномерные сетки whi2 = {xt = ihx,yj = jhy; г = 0,Nx,j = 0, Ny;Nxhx = Lx,Nyhy = Ly}, Ши^ = Ш = khg; к = 0,Ng; Nghg = 1}, где hx, hy, he — шаги по пространству; Nx, Ny, Ng — количество узлов по пространственным координатам ж, у, 9; и образуем пространственную сетку ши = ши12 х ши3. Дискретизация задач (14)–(28), входящих в расщепленную цепочку, осуществляется на пространственно-временной сетке шИт, шИт= ших штс помощью интегро-интерполяционного метода. Выражения Lc12C(1), L c3C(2), -О12С(1), -О3С(2) аппроксимируются соответственно разностными выражениями К12с, К3с, Л12с, Л3с интегро-интерполяционным методом на прямоугольной равномерной сетке с использованием функции заполненности ячеек. Имеем С1)(ж,у, е,о) = с0(х,у, е), (ж,у, е) е ши, при п = 0, (19) с”1) ^ с^2), (ж, у, e,tn) е Шит, п = 1,N - 1, сП+1 - СП.А ________ -^----^ = Л12ср+1 - К^1+ ф”, (ж, у, е) е Шит, п = 0, N - 1, С?2) = с”1+1, (ж, у, е) е шит, п = 0,N - 1, П+1 _ „п С(2) С(2) τ Л3СП2+1- К3СП+1+ ф”, tn Уравнения (22)–(24) дополняются выражениями с соответствующей аппроксимацией граничных условий (5)–(6), а уравнения (22)–(23) — условий (7)–(8). Для решения трехточечных разностных задач (25)–(26) применяются последовательные алгоритмы прогонки. Таким образом, на каждом временном шаге последовательно решаются две начально-краевые разностные задачи (19)–(21) с соответствующими граничными условиями на боковой поверхности и (22)–(23) с соответствующими граничными условиями на свободной поверхности и на дне. В качестве методов решения двумерной задачи на верхнем переменном слое будем использовать адаптивный попеременно-треугольный метод, который построен для случая ограниченного значения сеточного числа Пекле — Реи, Реи< 2; для морских и прибрежных систем данное ограничение выполняется с достаточно большим запасом.
3. Метод решения сеточных уравнений Наиболее ресурсоемкой частью программной реализации является численная реализация системы двумерных сеточных уравнений при аппроксимации ЛДС неявными схемами (схемами с весами) или при полной аппроксимации неявными схемами решения системы линейных алгебраических уравнений (СЛАУ). Для ускорения вычислений был разработан параллельный алгоритм, основанный на адаптивном попеременно-треугольном методе (ПТМ) решения СЛАУ и использующий технологию MPI для осуществления информационного обмена между вычислителями. В конечномерном гильбертовом пространстве Н рассматривается задача об отыскании решения операторного уравнения Аж = /, Л : Н ^Н, где Л — линейный, в общем случае несамосопряженный, положительно определенный оператор (Л > 0). Для нахождения решения задачи (24) будем использовать неявный итерационный процесс тт+1 „т В---------+ Лжт= /. (25) пт+1 В уравнении (25) т — номер итерации, пт+1 > 0 — итерационный параметр, а В — некоторый обратимый оператор, который называется предобуславливателем или стабилизатором. Обращение оператора В в (25) должно быть существенно проще, чем непосредственное обращение исходного оператора Л в (24). Оператор В построен, исходя из аддитивного представления оператора Л0— симметричной части оператора А и его кососимметричной части Ло = Ri + R2, Ri = R*, (26) где Л = Ло+ Л1, Ло= Л0, Л1 = —Л1 на основе симметричной части Лооператора Л. Оператор-предобуславливатель запишется в следующем виде В = (D + wRi)D-1(D + WR2), D = D* ш > 0, (27) где D — некоторый оператор. Соотношения (26), (27) задают адаптивный ПТМ решения сеточных уравнений [14], если определены операторы R1, R2 и указаны способы определения параметров пт+1, ш и оператора D.
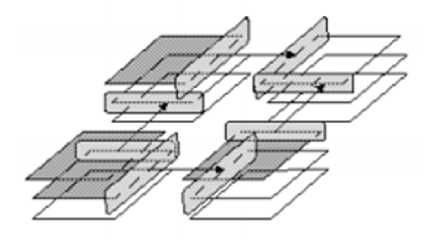
4. Параллельная реализация Программная реализация модели гидродинамики была осуществлена на языке C++ с использованием технологии MPI, что позволило провести ряд вычислительных экспериментов на многопроцессорной вычислительной системе Научно-технологического университета «Сириус». Использовалась часть кластера, построенная на основе открытого стека приложений OpenHPC, содержащая 1440 процессорных ядер по 2,3 ГГц и 10,24 Тб оперативной памяти. При параллельной реализации использованы методы декомпозиции сеточных областей для вычислительно трудоемких задач диффузии-конвекции, учитывающие архитектуру и параметры многопроцессорной вычислительной системы [5; 8; 10; 15; 20]. Декомпозиция расчетной двумерной области выполнена по двум пространственным переменным ж, у (см. рис. 2), а также использовалась декомпозиция по одному пространственному направлению (одной горизонтальной координате). Рис. 2. Декомпозиция двумерной сеточной области На первом шаге вычислений первый процессор обрабатывает верхний слой. Затем осуществляется передача перекрывающихся элементов смежным процессорам. На следующем шаге первый процессор обрабатывает второй слой, а его соседи — первый. Передача элементов после расчета двух слоев первым процессором показана на рисунке 3. Рис. 3. Схема для расчета вектора решений для системы с нижней треугольной матрицей В схеме для расчета вектора ут только первый процессор не требует дополнительной информации и может независимо от других процессоров вести обработку своей части области, остальные процессоры ждут результатов от предыдущего процессора, пока тот не передаст вычисленные значения сеточных функций для узлов сетки, располагающихся в предшествующих позициях данной строки. Процесс продолжается до тех пор, пока не будут рассчитаны все слои. Далее вычисляются скалярные произведения - Шт) = \ „• )2, (28) г (Лшт, шт) = £(ЛШт),(Шт)„ (29) г (Лшт, Лшт) = ^(Лшт)2. (30) г Каждый процессор считает свою часть скалярных произведений (28)–(30), затем осуществляется передача данных от всех процессоров (ядер) ко всем. Значение скалярных произведений будет равно сумме всех частичных сумм. С помощью формулы (28) осуществляется переход на следующую итерацию. Представим результаты численных расчетов. Были использованы расчетные сетки nN^ х kNy х N0, где параметры п и к определяют способ декомпозиции по двум (одному) из координатных горизонтальных направлений, nN'x = Nx, kNy = Ny, nk = p. В таблице 1 приведены зависимости времени моделирования от распределения процессоров по пространственным координатам (х,у, 0). Для расчетных сеток с числом узлов по трем координатным направлениям 200x200x100 и 1000x1000x100 узлов при разбиении расчетной области на p частей по одному пространственному направлению. В таблице 2 представлены полученные значения ускорения и эффективности в зависимости от количества процессоров для параллельного варианта попеременно треугольного метода. Здесь использованы обозначения: p — количество процессоров; п, к — количество подобластей по пространственным координатам х и у соответственно. Таблица 1 Результаты работы алгоритма — время решения в секундах — с использованием технологии MPI для различного числа вычислителей на двух расчетных сетках(схема расщепления — неявные ЛДС — ЛОС) Сетка/число процессоров 1 2 4 8 12 16 20 24 200x200x100 1,3167 0,7747 0,3401 0,2053 0,1392 0,1352 0,1118 0,0974 1000x1000x100 55,303 30,037 16,640 6,8903 4,6011 4,421 3,268 2,9 Таблица 2 Результаты работы параллельного алгоритма, построенного на основе декомпозиции расчетной области по двум пространственным направлениям (неявные схемы расщепления ЛДС — ЛОС) Р п к 200x200x100 1000x1000x100 время ускорение эффективность время ускорение эффективность 16 16 1 0,1352 9,74 0,6757 4,421 12,51 0,7818 16 8 2 0,1232 10,69 0,6854 3,52 15,71 0,9821 16 4 4 0,1123 11,72 0,7881 3,499 15,8 0,9878 20 20 1 0,1118 11,78 0,5891 3,268 16,92 0,846 20 10 2 0,1104 11,93 0,5965 3,203 17,27 0,8633 20 5 4 0,09686 13,6 0,6798 3,153 17,54 0,877 24 24 1 0,09744 13,51 0,5631 2,9 19,07 0,7946 24 12 2 0,09134 14,42 0,6007 2,846 19,43 0,8096 24 8 3 0,08365 15,74 0,6559 2,831 19,53 0,8139 24 6 4 0,07407 17,78 0,7407 2,77 19,97 0,8319 Коэффициент ускорения на прямоугольной сетке 1000x1000x100 узлов при числе использованных процессоров, равном 24, составил 19,07 раза (время исполнения для одного процессора — 55,30 с., для 24 — 2,9 с). В таблице 3 представлены зависимости времени выполнения одного шага алгоритма ПТМ от числа процессоров для двух расчетных сеток, содержащих: 500x500x100 и 1000x1000x60 узлов при декомпозиции расчетной области по одному пространственному направлению. Таблица 3 Время исполнения алгоритма в с. с использованием технологии MPI для различного числа вычислителей для двух расчетных сеток (ПТМ) Сетка 1 2 4 8 12 16 20 24 500x500x100 15,652 8,1459 4,1752 2,2188 1,5997 1,3111 1,0814 0,9720 1000x1000x100 38,16 19,690 10,210 5,3694 3,8203 3,1618 2,6823 2,5091 Результаты расчета ускорения и эффективности в зависимости от количества процессоров для параллельного варианта попеременно треугольного метода приведены в таблице 4. Коэффициент ускорения алгоритма при использовании прямоугольной сетки, содержащей 1000x1000x60 узлов и числе процессоров, равном 24, составило 15,2 (время исполнения для одного процессора — 38,16 с., для 24 — 2,51 с). Подводя итоги, можно сказать, что схема расщепления, использующая явную ЛДС и неявную ЛОС имеет преимущество при использовании относительно грубых сеток по горизонтальным направлениям для моделирования процесса переноса взвесей в прибрежных системах (500–1000 м, характерное число узлов по каждому из горизонтальных координатных направлений 200–400 м), по вертикальному направлению порядка 100 м. При использовании более подробных сеток (характерный шаг сетки 50–300 м по каждому из горизонтальных координатных направлений, характерное число узлов по каждому из горизонтальных координатных направлений — 1000 м и более) наилучшими являются неявные схемы расщепления ЛДС — ЛОС. Данные выводы применимы для относительно небольшого числа процессоров (немногие десятки) и в существенной мере зависят от архитектурных особенностей конкретной вычислительной системы. Таблица 4 Время выполнения параллельного алгоритма адаптивного ПТМ, построенного на основе декомпозиции расчетной области по двум пространственным направлениям, для численной реализации двумерной разностной схемы, входящей в аддитивную схему ЛДС — ЛОС р п к 500x500x100 1000x1000x60 время ускорение эффективность время ускорение эффективность 16 16 1 1,311 11,94 0,7461 3,162 12,07 0,7543 16 8 2 1,288 12,15 0,7594 3,004 12,7 0,794 16 4 4 1,284 12,19 0,7619 2,987 12,78 0,7985 20 20 1 1,081 14,47 0,7237 2,682 14,23 0,7113 20 10 2 1,033 15,16 0,758 2,547 14,98 0,749 20 5 4 1,023 15,3 0,7652 2,499 15,27 0,7635 24 24 1 0,9721 16,1 0,6709 2,509 15,21 0,6337 24 12 2 0,9629 16,26 0,6773 2,246 16,99 0,708 24 8 3 0,9462 16,54 0,6893 2,242 17,02 0,7091 24 6 4 0,9316 16,8 0,7001 2,241 17,03 0,7095 Заключение В статье рассмотрено построение и исследование параллельных алгоритмов для реализации 3D-модели транспорта взвесей в прибрежных морских системах на основе ЛДС расщепления. Проведено сравнение параллельных алгоритмов, использующих ЛДС с явной и неявной аппроксимацией двумерных задач, входящих в аддитивную схему. Для численной реализации применен адаптивный ПТМ, разработанный ранее в авторском коллективе для разностных задач уравнений с несамосопряженным операто- ром для ограниченного числа Пекле (Peℎ < 2). Для моделирования динамики транспорта взвеси прибрежной системы разработан программный комплекс. На многопроцессорной вычислительной системе НТУ «Сириус» исследована параллельная реализация программного комплекса, выполненная на языке C++ с использованием технологии MPI. Результаты работы параллельного алгоритма, построенного на основе декомпозиции расчетной области по двум пространственным направлениям, позволили оценить его эффективность.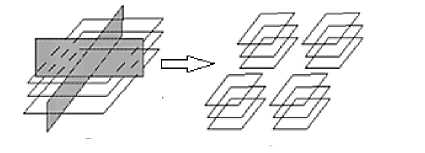
Список литературы Локально-двумерные схемы расщепления для параллельного решения трехмерной задачи транспорта взвешенного вещества
- Сухинов, А. И. Двумерные схемы расщепления и некоторые их приложения / А. И. Сухинов. - М. : Макс Пресс, 2005. - 408 с.
- Сухинов, А. И. Математическое моделирование транспорта наносов в прибрежных водных системах на многопроцессорной вычислительной системе / А. И. Сухинов, А. Е. Чистяков, Е. А. Проценко // Выч. мет. программирование. — 2014. — Т. 15, вып. 4. — C. 610-620.
- Сухинов, А. И. Построение и исследование корректности математической модели транспорта и осаждения взвесей с учетом изменения рельефа дна / А. И. Сухинов, В. В. Си-дорякина // Вестник Донского государственного технического университета. — 2018. — Т. 18, № 4. — C. 350-361. — DOI: https://doi.org/10.23947/1992-5980-2018-18-4-350-361.
- Численная модель динамики поверхностных вод в русле Волги: оценка коэффициента шероховатости / А. В. Писарев, С. С. Храпов, Е. О. Агафонникова, А. В. Хоперсков // Вестн. Удмурт. ун-та. Матем. Мех. Компьют. науки. — 2013. — № 1. — C. 114-130.
- Belotserkovskii, O. M. Decomposition method applied to the solution of problems of viscous incompressible fluid dynamics / O. M. Belotserkovskii, V. A. Gushchin, V. V. Shchennikov // Computational Mathematics and Mathematical Physics. — 1975. — Vol. 15. — P. 197-207.
- Coastal hydrodynamics in a windy lagoon / E. Alekseenko, B. Roux, A. Sukhinov, R. Kotarba, D. Fougere // Nonlinear Processes in Geophysics. — 2013. — Vol. 20. — P. 189-198. — DOI: https://doi.org/10.1016/j-.compfluid.2013.02.003.
- Flood-based analysis of high-magnitude sediment transport using a non-parametric method / T. Francke, J. A. Lopez-Tarazon, D. Vericat, A. Bronstert, R. J. Batalla // Earth Surface Processes and Landforms. — 2008. — Vol. 33, iss. 13. — P. 2064-2077. — DOI: https://doi.org/10.1002/esp.1654.
- Kovenya, V. M. Application of Splitting Algorithms in the Method of Finite Volumes for Numerical Solution of the Navier-Stokes Equations / V. M. Kovenya, P. V. Babintsev // J. Appl. Ind. Math. — 2018. — Vol. 12. — P. 479-491. — DOI: https://doi.org/10.1134/S1990478918030080.
- Leontyev, I. O. Coastal Dynamics: Waves, Moving Streams / I. O. Leontyev. — Moscow : GEOS Publ., 2001. — 272 p.
- Milyukova, O. Yu. Parallel approximate factorization method for solving discrete elliptic equations / O. Yu. Milyukova // Parallel Computing. — 2001. — Vol. 27, iss. 10. — P. 1365-1379. — DOI: https://doi.org/10.1016/S0167-8191(01)00092-8.
- Ouda, M. Development of a new multiphase sediment transport model for free surface flows / M. Ouda, E. A. Toorman // International Journal of Multiphase Flow. — 2019. — Vol. 117, iss. 3. — P. 81-102.
- Predictive modeling in sediment transportation across multiple spatial scales in the Jialing River Basin of China / X. Liu, S. Qi, Y. Huang, Y. Chen, P. Du // International Journal of Sediment Research. - 2015. - Vol. 30, iss. 3. - P. 250-255. - DOI: https://doi.org/10.1016/j-.ijsrc.2015.03.013.
- Samarskii, A. A. Finite-difference approximations to the transport equation. II / A. A. Samarskii, P. N. Vabishchevich // Differential Equations. - 2000. - Vol. 36. -P. 1069-1077. - DOI: https://doi.org/10.1007/BF02754509.
- Sukhinov, A. I. Adaptive modified alternating triangular iterative method for solving grid equations with a non-self-adjoint operator / A. I. Sukhinov, A. E. Chistyakov // Mathematical Models and Computer Simulation. - 2012. - Vol. 4, iss. 4. - P. 398-409.
- Sukhinov, A. I. Increasing efficiency of alternating triangular method based on improved spectral estimates / A. I. Sukhinov, A. V. Shishenya // Mathematical Models and Computer Simulations. - 2013. - Vol. 5. - P. 257-265. - DOI: https://doi.org/10.1134/S2070048213030101.
- Sukhinov, A. I. Locally two-dimensional schemes for the approximation of the three-dimensional heat equation in toroidal coordinates / A. I. Sukhinov, V. S. Vasil'ev // Russian Mathematics (Iz. VUZ). - 1996. - Vol. 40, iss. 3. - P. 58-67.
- Sukhinov, A. I. Numerical realization of the three-dimensional model of hydrodynamics for shallow water basins on a high-performance system / A. I. Sukhinov, A. E. Chistyakov, E. V. Alekseenko // Mathematical Models and Computer Simulations. - 2011. - № 3. -Article ID: 562. - DOI: https://doi.org/10.1134/S2070048211050115.
- Sukhinov, A. I. Reconstruction of 2001 Ecological Disaster in the Azov Sea on the Basis of Precise Hydrophysics Models. / A. I. Sukhinov, A. A. Sukhinov // Parallel Computational Fluid Dynamics. - New York : Elsevier Science Inc., 2005. -P. 231-238. - DOI: https://doi.org/10.1016/B978-044452024-1/50030-0.
- Sukhinov, A. I. Uniqueness of solving the problem of transport and sedimentation of multicomponent suspensions in coastal systems / A. I. Sukhinov, A. A. Sukhinov, V. V. Sidoryakina // Journal of Physics: Conference Series. - 2020. - Vol. 1479. - Article ID: 012081. - DOI: https://doi.org/10.1088/1742-6596/1479/1Z012081.
- Two-Phase Porous Media Flow Simulation on a Hybrid Cluster. / M. Trapeznikova, B. Chetverushkin, N. Churbanova, D. Morozov // Large-Scale Scientific Computing. LSSC 2011. Lecture Notes in Computer Science. - Berlin, Heidelberg : Springer, 2012. -Vol. 7116. - P. 646-653. - DOI: https://doi.org/10.1007/978-3-642-29843-1_74.


