Локально-одномерная схема для уравнения теплопроводности с краевыми условиями третьего рода

1. Локально-одномерная разностная схема

В цилиндре Q t = G х (0, T] , основанием которого является прямоугольный паралле-

лепипед G = { x = (x 1 , x ₂ ,..., x p ) : 0 < x _a < ' _a , задачу:

а = 1, 2,..., р } с границей Г , рассмотрим

где

I

|u = Lu ⁺ f^{( x,t )}, k a (x, t) dx a = в - а (х, t) u(x, t)

(x,t) G Q t ,

^ - a (x,t),

- k a (x,t) dX a = e + a (x,t) u(x,t) - ^ ₊ a (x,t), u(x, 0) = U o (x),

xa = 0, xa — 'a,

p

Lu = У^ L _a u, L _a u =

q a (x,t)u,

k _a (x,t) , q _a (x,t) , f(x,t) , e ± _a (x,t) — заданные функции x и t такие, что

0 < co 6 ka (x,t) 6 ci, |qa |, |e±a | 6 C2, ka(x,t) G C 3,1(Q T), qa(x,t),f (x,t) G C 2,1((Q T), а = 1, 2,...,p, где Qt = G х [0,T], G = G + Г, Cm,n — класс функций, непрерывных вместе со своими частными производными порядков m и n по x и по t соответственно. Такие несколько завышенные условия гладкости потребуются при построении разностной схемы второго порядка аппроксимации.

(с) 2011 Баззаев А. К.

Задача (1)-(3) рассматривалась в работе [1] в случае, когда q _a > q * > 0 , P ± _a >  0 , в - _а +в + _a > 0 , а = 1, 2,... ,p . А в работах [2] и [3] рассматривались локально-одномерные схемы (ЛОС) для нагруженного уравнения теплопроводности и для уравнения диффузии дробного порядка соответственно.

Пространственную сетку выберем равномерной по каждому направлению Ox _α с шагом h _a = ' _a /N _a , а = 1, 2,...,p .

Ш а — {x a — ia h a • i a — ^{0 , 1}, • • • , N a }, ^D h — Y Y ^D a , a =1

p

Da    ^xa      iaha • ia   1,... , Na   1 J*,   ^h    Y | Da a=1

~ α

hα, ha/2,

i a = 1, 2,...,N a - 1, i _a = 0, N _a ,

ω _α — множество внутренних по отдельному направлению x _α узлов, γ _α — множество граничных по отдельному направлению X a узлов, O a — множество всех внутренних и граничных по отдельному направлению x _α узлов, ω _h — множество всех внутренних узлов, Ш h — множество всех внутренних и граничных узлов (по всем направлениям вместе).

На отрезке [0,T] также введем равномерную сетку о т = { t j = jT, j = 0,1,...,j o } с шагом т = T/j o . Каждый из отрезков [t j ,t j +i ] разобьем на p частей, введя точки t j + 2 = t j + ^с т , а = 1, 2,... ,p — 1 , и обозначим A _a = (t j + a - 1 , t j ₊ 2] , а = 1, 2,...,p .

Уравнение (1) перепишем в виде

p

£ PaU = 0, a=1

„       ^{1 d}u              P          P P

PaU =- —: - LaU — fa,     fa = f pdt             a=i

Будем последовательно решать задачи [6]

1 dv ( a )    ,            P     „    . X

^P a v ( a )     p dt     L a v ( a )    ^f a    ⁰,   t € ^A a , ^а 1, ², . . . , p,

I

ka dxa    e—av(a)   Ц-a, i dv(a) __ п kKa dxa = P+av(a) — P+a,

xa = 0, xa — 'a,

полагая при этом

V (1) (x, 0) = u o (x),

v ( a )

^x , t j + 2 — 1 )     ^v ( a - 1)

^; j + ^ ) ,

а = 2, 3,... ,p,

" j + 2 - 1 ^{,t j +} 2]

луинтервале

j + ^a     j + ^{a — 1}

yJ P — yJ   P

τ

= Л a У ^{j + p} + P c + ^P ,

а = 1, 2,... ,p,

ЛСУ — (aayXa )Xa   day, где коэффициенты aα — сеточные функции, которые выбираются из условий второго порядка аппроксимации на равномерной сетке. Можно использовать следующую аппроксимацию коэффициентов ka(x,t) [6]:

a _a = k _a (x i , • • •

X a - 1 , X a

⁰•^{5 h} a , x a +l ix p it), t — ^t j +1 / 2 •

К уравнению (7) надо присоединить граничные и начальные условия. Запишем раз- ностный аналог для граничных условий (5):

j+a        j+a a ")УхаО = в-аУо   - P-a,      xa = 0, л j +a            j +a                                                (8)

_- a "  ^y x _a N _a = ^e + a y N _a ^P - Ц + a , x a = ' a •

Условия (8) имеют порядок аппроксимации O(h _a ) . Повысим порядок аппроксимации до

O(h a ) на решениях уравнения (4) при каком-либо а [7]:

м л j + ^а             j + ^а               .

a “ v ( a ) X a , 0 = ^{5 a} v ( a ) , 0 — ^{p - a + O (}h ^{a );}

a° - ) =k ( a > = k + . h ^ +k- hi+ O(h a );

"^ -"^ = *W.,0 = v(a) + v"a) hY + O(ha); a(1°)v(a)x„ ,0 = k(a)v(a),0 + (k(a) v(a) )' hf + O(ha)S j +a

^{k (,)} v ( a ) = a ⁽¹ - ) v ( a )X„0 - 0.5h a k ■ v^) ⁰ + O(h a )

j + a

∂vp p da   + qav(a) - fa^+ O(ha),

„0 . = ^d V ( ^a l „00 . = ^{d 2} v (a)   _k 0 = 8кИ   k = дЧИ

( a )       8x _a ^,    ( a )       dxO.  ^,           dx _a ^,            dx ^,   ^.

Итак, j+a               j+a                          j+a

a ^{(1 a )} V ( a ) x _a , 0 - 0.5h a I v ( a ) t p + q a V ( a ) - f a = e - a V ( a )f0 - ^ — a + O(h a ) + O(h a T )•

Отбросив величины порядка малости 0(^ 2 0 ) и O(h a т ) и заменив V ( a ) на у , перепишем (9) в следующем виде:

j + ^a           j + ^а         j + ^а

О-МУха0 - 0^5hay;-,0 p = e-ay0 p - ^-a — 0^5hafa,0, Xa = 0, или

j + , Ую p

a ) j+a ^{а (1 а )} У х„ 0

-

-   j+a в-a У0 p

0^5h a

⁺ ^ - a ,

x _a = 0,

P — a = ^-T" + f a, 0 ,   в - a = в - a + 0^5h a d ^ •

0•5h _a

Аналогично при xa = 'a имеем j+ P         j+P j + P _ a( У-«К + e+ayNa , _ ytNa =        0Ж       + P+ai где p+a = 0^+p + fa,Na, f^+a = в+a + 0^5had^a")

Итак, получили разностный аналог задачи (4)–(6):

y

j + ^a p

_

t

^Л ( а ) y j ⁺ p + ³ p

y

3+a p t,0

a ^{(1 a} )

j+a y XaO

j + a N

a = 1, 2,... ,p, xa G wa, xa — 0, xa — 'a,

α

3 j ⁺ p ^в - а ^у 0

_

0 . 5 h a

_a (Na)

-

y

^α j_p

x a ,Na

⁺ p - a ,

j+ a + e +a y N _a ^P

0 . 5 h a

^{+ p} + a ,

y(x, 0) — u o (x)

или в краткой записи ytta) — Л a y^ +$a+ P , a — 1, 2,...,p, x G Wh, y(x, 0) — uo(x),

где

A a y ^{( a )} —

A a y ^{( a )}

Л - y ^{( a )}

A+y ^{( a )}

Ф

3+ a p α

(aay^A   - da y(a), xα n (1a)7/a) _t   7/(p)

a    ^y xa,0 ^e -^P y 0

0 . 5 h a           ,

- a ⁽N“ + в +« У^ 0 . 5 h a

3 + p

^ a    , x a ^{G W} a ,

< p-a,    Xa — 0, p+a,   xa — 'a •

xα ∈ ωα, xa — 0, xa — 'a,

z ^{j +} p

-

j + ^{2 - 1} z ^p

τ

— K a Zj ^{+ p} + ^j p ,

j+p        j+a     j+a где ^a p — AauJ p + ^ p

-

u ^{j +} p

-

a - ¹ u ^{j +} p

Обозначая

τ

◦ ψ α

L a u ⁺ f a

1 du V^{+ 1} p ∂t

o                                                      j + a     ◦     *

и замечая, что J2a =l ^ a — 0 , если J2a =l f a — f , представим ^ a — ^ a ^p — ^ a + ^ a . Тогда

ψ

j+a p α

— A a U ^{j + p} + ^ a ^p

-

u ^j+ p

-

j + ^{3— 1} u ^p

τ

◦◦

+ ^ a — ^ a

◦

^— ^ a +

A _a u ^{j +} p

— L a U ³^ ² ) + (^ ja ^{+ p} — f ³a^{+ 1} ) —

u j⁺ p

-

3 + ^{3— 1} u ^p

-

τ

1 / du V⁺ 2 p ∂t

◦      *

— ^ a + ^ a

Г X    j + а где фа = Ла u p

- L a u ^{j + 1} ) + ( ^j p - f j ¹ )

-

_u j+αp

_{j +} α - 1 u ^p

τ

1 ( ddu ) ^{j +} 2

Очевидно, что ф: = o(i).

ФГ = O(h2 + T), pp ф = Ефа = Еф: = о (ihi2+E а=1      а=1

Запишем граничное условие при x _a = 0 следующим образом:

0.5^у - ^{а )} = a ^{(1 a} ) y Xa ) - в - а У о + 0.5h_af a, c + Ц - а . t                   α,0

Пусть z ^{j + p} = y ^{j+ p} - u ^{j+ p} , где u — решение исходной задачи (1)-(3). Подставим y ^{j+ p} = z j p + u ^j+ p в (11). Тогда получим

0.5h a z - + p = а а 1 а - 0.5h a d a о u j p

A j + a         j + a               j + a         j + a ) Z xa P 0 - в - а Z 0 p - 0.5h a d a, 0 z 0 p - в - а ^ о p - 0.5h a u - + a + а а 1 а ) u^ + 0.5h a f a, о + Ц - а .

К правой части полученного выражения добавим и вычтем

Тогда

Ф - а

О

0.5h_a ф _{- а} = 0.5h _a

∂ ∂x α

∂u k _α

∂x _α

^{- q} _a u ⁺ f a

j + ^a\        x j + ^a          j + ^a

= 0.5h_a f _a - u - ^P + a u     - в - а ^ о p -

- 0.5h a

∂ ∂x α

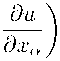
1 dul ^{j+ 1}

p dt] о

0.5 h_ctda, 0 U 0 p + Ц - а

„     1 dul ^{j +}2       , О

- qctu + fa---777     + 0.5ha ф-а p ∂t

j + ^a\            j + ^a

= 0.5h_a f _a - u - ^p    + a'. ) u X a,P

j +

^{- в} - a ^u о

- O.5h_ctd a, оUо p + Ц - а

- 0.5h a

∂     ∂u

k

∂x    ∂x _α

" ^{j +} 2         /

- 0.5h_a f a

j + ^a \                  j + ^a      ,     ,              ^О

- u - p ) + 0.5h_aq_au o p + O(hctT )+0.5h_a ф _-а

/1 \ j + ^a            j + ^a

= a ⁽ _a ^{1 a} u x a,0 - в - a U ₀ p + Ц - а - 0.5h a

k α

du ^{j +} p ∂x α

∂

+ 0.5ha7:--

∂x _α

/ o \ j + ^a

∂u p kα

∂x _α

∂ ∂x α

∂u

"a 77

∂x _α

1 j + 1

О

+ 0.5h_a ф _{- а} +O(h_aT )

j +

^{- в} - a ^u 0

⁺ Ц - а

-

α

_n ^d Л ^du v⁺ p 0.5h_a-— катт— ∂x ∂x _α

+ 0.5h_a Ф - а +O(h 2 ) + O(h«T ) =

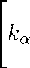
du ^j+ p ∂x α

j +

^{- в} - a ^u о

⁺ Ц - а

X a =0

+ 0.5h_a ф - а +O(h«T )+ O(h 2 ).

В силу граничных условий (2) выражение, стоящее в квадратных скобках, есть нуль.

Поэтому Ф - а = 0.5h_a Ф - а +ф - а , Ф - а = O(h 2 + T ) + O(h_aT ).

Итак, j+а      (л A j +а    -     j+а              О .

0.5h_az t, 0 p = a£ ^{1 a )} z X _a , 0 - в - а z 0 p + 0.5h_a Ф - а +Ф - а .

Или j +a          X, a zt,0 p =Aaz p + ф-a, Ф-а = Ф-а -05^- *

Аналогично при xa = 'a имеем j+a        j+a p           p ziNa = ЛХ + Ф+а, ф+а = ф+а ■ 0^ *

3. Априорная оценка

Умножив уравнение (10) скалярно на y ^{j + p} = y ^{( a )} , получим

[yia),y(a^ - [Лay(a),y(a)] = [ф(а),у(а)] , где p                 Nα

[u,v] = У^ UvH, H = Ц ~ a , [u,v] a = 5 " /.. V i a ~ a *

x E H h              a =1                 i _a =0

Преобразуем каждое слагаемое тождества (14):

' ] =2' H L , < » h ) ) i +T ■ H L , ( » h > ;

[Л a y ^{( a )} ,y ^{( a )} ] _a = (Л а У ^{( а )} ,y ^{( a )} ) _a +Л — у О ^{а )} у ^{( а )} ~a + Л + у ^⁰^ y^ ~ a

= (U e y / a ) ,y ^{( a )} ) - (4 * “ V^{a )} ,y ^{( a )} ) +Л — У ^{( а )} .y ° ~ a +Л + y ^(a) y N ~ a xα      α         ^α

₌  (_п -1.2 ]      ((7⁽ⁱ“⁾?/^(a) ?/^a)) a^(Na)u- м ?/^a)  о^(1а)?у ?/^a)

a O ,y i a^     ^da У ,У J ⁺ a a ^y X a ,N a ^y N _a a a ^у Х а,0 ^У 0

• ^{+ а} а ^1а) у Х ^{0 )} о y 0 ^{a )} — /3 - a y 0 ^{a )} y 0 ^{a )} - a aN ^{a )} y X ^{a )} ,N _a y N - ^e + a (y N )

• =    - ( aa.y i a ] a ^- (da i " ⁾ y ^{( a ) ,} y ^{( a )} ) _a ^{- e} - a (y 0 ^{a )} ) ^{- e} + a (y ( N ) )

  - O.bh^y ⁽ 0^a) - O.bM N ^N o )

• —    _ f_a y² 1 _ [ 4^{( i} a ⁾y^{( a )} y^{( a )} ] _ 4    (y^{( a )})²_ 4,   (y^{( a )})²

• =    a-ciy У а _aJ_a det ^y ,^y J_a P- a ^^y 0 J P + a y ^y N_aJ "

[ф ^{( a )} y^{(a )}] — L^{( a )} y^{(a )} ] + и y^{(a )} + и , y^{(a )}

• L ^ , ^y -la = L^ , ^y _| a ⁺ ^ - a ^y 0 ⁺ ^ + a ^y N _a *

Просуммировав (16) и (17) по всем i s = i _a , s = 1, 2, * * *,p , получаем

N

[Лa y ^{( a )} ,y ^{( a )}] = У2 I 52Л a y ^{( a )} y ^{( a )} ~ a 1 H/ ~a i s = i a i a —⁰                   /

• =    - X f( a« ^, y X a 1 a + [ ^{d (} i ^{a )} y ^(a) ,y ^{( a )} ] _a + ^e - a (y ^{( a ) |} i a =0 ) ² i s = i a

+e + a (y ^{( a )} | i a = N a )²} H/~ a ,

[ ф ^{( о )} ,y ^{( a )} ] = X Q^ ^{( a )} ,y ^{( a )} ] _a + ^ - a y ^{( a )} | i =0 + ^ + a y ^{( a )} | i = N K/ ~ a * i _s = i

Подставляя (15), (18) и (19) в тождество (14), получаем

(l ^{| y ( a )} L( .h )) _t ^{+ т} “ye ( -» ⁺c ^o l l ^{y X a )} l lL. 2 ( =>h )

⁶ [^ ,y ^{( a ) ] +} X :     ■ • ' .     ⁺      ■' ) H -

i s ^_ i a

-hda y^     ] - X (e-a(y(a)|ia=o) + e+a(y(a)La=Na) )H/~a • is _ia

Оценим слагаемые, стоящие в правой части (20):

,y ^{( a )} ] 6 2 p^{a )} | |

L 2 ( - h )

+2 |y ^{( a )} lU

X f^ - a y ^{( a )} | . __o + ^ + a y ^{( a )} | . _ N p/ ~ a i s ^_ i a

/ X f^ — a I ^ + a , (у^Н l i a _o ) ² , (y^H l i a N a ) ² \

6               2 +2+2)H/~a is _ia

⁶ 2 X (^ a Ct j ^{) +} ^ + a ^{( t} j ^HA a i s ^_ i a

+ XElAlL,+(r+1 )l|y ^{( a )}L ,)h/ ~ "

II L2(a) у'a E/ II      llL2(a)/ is _ia

= | X (^At j ^{) +} ^ + a ⁽t j ⁾ } H/~^ a ⁺ еЦу Х^ | ¹          ( ^T ^{+ 1} )l ¹ y ^{( a )} | ¹ J

2                                                         IIL ₂ ( - h ) \'a E/И IIL 2 ( - h )

i s ^_ i a

- [d a y ^{( a )} ,y ^{( a )}] 6 C 2 ¹ 1y ^{( a ) 1} 1        ;

L 2 ( - _h )

- X ( ^{в - а} ( ^{y ( a ) |} i _a _o ) ^{+ в + а} ( ^{y ( a )} L_a _ N a ) ) ^H/ ~ ^a i s ^_ i a

2C 2  ||y ⁽" 11

L 2 ( - h )

+ 2c2< 1 + ¹) ! | y^{( a )} 1 1 ²₍ , V 'a E у W llL 2 ( - h )

где k^k L ₂ ( _a ) означает, что норма берется по переменной x _a при фиксированных значениях остальных переменных,

11 уХа 11

L 2 ( - h )

= Е 1 1 уХ? 1 1 i s ^_ i a

H/~ α ,

L 2 ^{( a )}

l ^{1 У Х} “ । ¹ L 2 ( a )

N α

= EyX a ~ a . i a ^_ l

Подставляя неравенства (21) и (22) в (20), находим

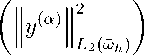
^{+ C} 0

1    1^

' a ⁺ e)

t

11 Уха 11

L 2 ( - h )

1 k(a)||²

2 ^{11 W 11} L 2 ( - h )

+(2 +

+ C 2 + 2C 2

1     1

' a ⁺ e

L 2 ( - h )

^{+ (2 c} 2 ^{+ 1) e 1 1 y} X a ^{1 1       +} 9 X (^ ² a ⁽t j ⁾⁺ ^ + a ⁽t j )) ^H/ ~ a

L 2 ( - h ) 2

i s ^_ i a

Положим

—    co e = 2(1 +2C2),

^c 3 ^— ~ ⁺ c 2 ⁺ ( T1) ^{(1 + 2}c 2 )- 2            \ 'Ct ^ )

Тогда неравенство (23) можно переписать в виде j+ al I2            II j+ — I I2         I co II (a) II2

fly p ) ^- lly p L■^т fly * * IL^

⁶ iUlL" >⁺ c 3 ^T I ly^ 'IlL- >^{+ T} X ^{, p 2} " ⁺ ^ + a )H/ ~« •

2 11        IIL2 ( ^ h)          II        HL2 ( ^ h) 2

i s = i a

Просуммируем (24) сначала по a — 1, 2, • • •, p :

pp

11 y ^{j +1} 11 L 2 (.,) + f т X 1 1 y£ ) 1 1        611 y 11 ² . . + C 3 т E11 y ^{( a )} 1 1 L 2

a=1

pp

+ iXll^ 11 _Ll- , + ТЕ E( ^ - a + 2. » ~. ,

2    ' II      IIL2(..)    2' “ a=1                    a=1 is=ia а затем по j' от 0 до j:

jp0α fl yj+4U) + co X т XI j7 I II j0=" a=1

jpjp

6 11У ⁰ lU > + C 3 X Т X | j ' 1 1 l (_й) + 2 X Т X | И⁺ ' 1 1 l _(ЗД (25)

j0=o a=1             2V h)      j0=o a=1

+ 12 ^X Т ^X X (^ ² - a (tj-)+ ^ + a (t , 0 )W~ a .

j ⁰ =o ^a =1 i s = i a

Из (25), пользуясь дискретным аналогом леммы Гронуолла (см. [4, с. 171]) при малых т 6 To, находим требуемую оценку jp           jp

11 y ^{j +1} ll L 2 ( . h ) + X т X| | j p 11 L (_Зд 6 M 11 y " 11 L 2 (* h ) + X т X| | j ^p| I L j ⁰ =o a =1             ^{2 h}                           j ⁰ =o a =1             ^{2 h}

jp

+ E т££ (^ ² a (t j 0)+ ^ + a (t j 0))H/~ a , j ⁰ = o ^a = 1 i s = i a                                    2

где M зависит от размерности области.

• 4.    Сходимость ЛОС

По аналогии с [5, с. 528] представим решение задачи для погрешности z ^{j +} p :

Z*a) —ЛaZ(a) +Ф'а+ p , где

Л а

^Л а ,  x a ^ ^ a ,

^Л a , x a   ⁰,

Л+, X a — ' a ,

j + ^a ^ a p

ψ α ,

^ - a ,

^ + a ,

x α ∈ ω α , x _a — 0, x _a — ' _a ,

0*0

^ a — ^ a + ^ a ,  ^ a

*

O(1), ^ a — O(h a + т ),

Ф - а

= Ф - а +

ψ

, *

-

α

0.5h a ,

^ф + а

- ° + ^{Ф+ а}

= ^{Ф + а +}0.5h a ,

Ф ± а = O(h l ) + O(h a T ), X Ф ± а = 0, а =1

в виде суммы z ( _а ) = v ( _а ) + П ( _а ) , Z ( _а ) = z j ⁺ p , где П ( _а ) определяется условиями

( Д—/ = ф . , x _е + Y а , а = 1, 2,... ,p, (n(x, ⁰⁾ = 0,

°

Ф а

Ф а ,

Ф - а ,

Ф + ^° а ^,

x α ∈ ω α ,

Х _а = 0,

Х а — 'а *

Из (27) следует, что n ^j+1 = П ( _Р ) = n j + т Ф 1 ° + Ф ₂ ° + ... + ф _р ° J = n j = - - - = П 0 = 0. Функция V ( _а ) определяется условиями

V(а) ,       =ЛаV(а) +Фа, Фа = ЛаП(а) + Фа, Ха G Ша,(28)

=Л-V(а) +Ф-а, Ф-а = Л-П(а) + Ф^/, Ха = 0,(29)

Т 0•5h

=Л+v(а) +Ф+а, Ф+а = Л+п(а) + ,.,', Ха = 'а,(30)

Т 0•5h

v(x, 0) = 0.(31)

Решение задачи (28)–(31) оценим с помощью оценки (26)

jp

Е тЕИ$ . « L , _Ph )

j 0 =0 а =1

j p _{0 α}

H v j +i H ²      + у т У ^ v j ⁺ p || 2

"     " L2 '^ ) фф ^ И x ^a H L ₂ ( ^ h )

j 0 =0 а =1

jp

+ Е т£ £ (Ф ² а (t j 0 )+Ф + а (t j 0 )) Н/~ а j 0 = 0 ^а = 1 i Y = i a

где

*

^Ф - а = ^Ф а ^{+ а} а ^1а ) (П ( а ) ) _х „ ^{- в} - а П ( а ) , 0 ^- d ^ П ( а ) , 0 = ^О ( Ь-а ^{+ т} ), ^x α,0

*

^Ф + а = ^Ф а ^{- а (}а ^а) (П ( а ) ) _х „ ^{- в} + а П ( а№ ^- d^ n ( а ) ,N a = ^О ^ ^ а ^{+ т} )- α,N_α

Так как n ^j = 0 , П ( _а ) = О(т) , k z j k 6 k v j k , то из оценки (32) следует следующая

Теорема. Пусть задача (1)-(3) имеет единственное непрерывное в Qt решение u(x, t) 2        4         3      ∂2 f и существуют непрерывные в Qt производные ddtu, dXOUxV, d^Xaudi, dxff, 1 6 a, v 6 p. Тогда разностная схема (10) сходится со скоростью O(|h|2 + т), так что

|| y ^{j +1} - u ^{j +1} « 1 6 M ( | h | ² + т ), | h | ² = ~ 1 + ~ 2 + ... + ~p,

где

j p _{0 α}

|yj+1K = |yj+1|L1(ih) + У т У |yia+ P И j0=0 а=1

.

L , ( ^ h )