Локальные свойства решений задачи коши для квазилинейного параболического уравнения второго порядка
Автор: Тедеев Александр Федорович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.10, 2008 года.
Бесплатный доступ
В данной работе рассматриваются задачи Коши ньютоновской упругой фильтрации и изучается поведение разности решений уравнений при разных режимах.
Слабое решение, задача коши, локальная оценка, оценка градиента
Короткий адрес: https://sciup.org/14318244
IDR: 14318244 | УДК: 517.955
Текст научной статьи Локальные свойства решений задачи коши для квазилинейного параболического уравнения второго порядка
Пусть x =
(
x
i
,...,x
n
)
g
R
N
,
N
6 1,
S
t
=
R
N
x(0,T), 0
Рассмотрим в области ST задачу Коши для уравнения ньютоновской упругой фильтрации uT — div(|Du|p 2Du) = 0, p > 2, u(x, 0) = uo(x).
Вместе с уравнением (1) будем рассматривать задачу Коши для уравнения:
V t — div( | Dv | q - 2 Dv) = 0, q> 2, v(x, 0) = v 0 (x).
Для определенности будем предполагать p > q .
В данной работе оценивается разность w = u — v решений (1) и (2) в некоторой норме L ^ (B p) в зависимости от близости начальных данных и близости p и q. Здесь всюду рассматриваются только положительные решения уравнений (1) и (2).
В доказательстве основной теоремы используется метод предложенный в [1], а также некоторые результаты работы [2].
-
2. Некоторые вспомогательные результаты и обозначения
Обозначим через
X ioc ( S t ) = L Poc (0, T ; W^ R N )), Y^S t ) = L qoc (0, T ; W^ q ( R N )),
0 0 1 ,p
X loc ( S T ) = {^ G X ioc (S T ) : ( 3 r> 0) V G L p oc (0 ,T ; w )( | x | <гц, (3)
Y
loc
(
S
t
)
= n
^
G
Y
ioc
(ST
) : (
3
r > 0)
v
G
L
qoc
(0,T;
W"'"
)(
|
x
|
(° 2008 Тедеев А. Ф.
Измеримую функцию u : St ^ R+ назовем слабым решением уравнения (1), если для любого £ eX (St ) выполняется соотношение
П { u T е+ | Dur 2 Du De ) d^ = 0. (4)
S T
Аналогично определяется слабое решение для уравнения (2).
Если | Du | E L poc (S T ), u T E L 1oc (S T ), то приведенное определение слабого решения уравнения (1) эквивалентно следующему:
Функция и — является слабым решением уравнения (1), если для любых ф E Xioc(St) и £ E Cq°(St) имеет место равенство jj ©uT(ф — и)+е + |Du|p 2 ВиВ[(ф — и)+е]} dxdT = 0, (5)
ST где п х \ 0 ф 6 u’
( ф - и ) + = < . .
ψ - u, ψ > u.
Доказательство эквивалентности определений (4) и (5) приводится в [1] для случая 1 < p < 2. Для случая p > 2 доказательство полностью повторяется и мы не будем его приводить. Пусть х ^ ф(х) — гладкая срезающая функция в B (i+ CT )p , ст > 0, такая, что s(х) = 1, х E Bp, s(х) = 0, | х | > (1 + a)p, 0 6 s(х) 6 1, |Ds | 6 (стр) - 1 .
Полагая в равенстве (5) £ = s p , мы получим
t j j ©uT(ф — u)+sp + |Du|p-2 ВиВ[(ф — u)+sp]} dxdт = 0.(6)
s R N
Здесь всюду мы будем предполагать выполненными условия
C1 u(x,t) 6 дидх t) 6 C2u(x,t),(7)
C1v(x,t) 6 ^vd^^’t) 6 C2v(x,t),(8)
c i и C 2 — положительные постоянные.
В дальнейшем все несущественные постоянные мы будем обозначать одной и той же буквой c.
Имеет место следующая
Лемма 1. Если и — решение уравнения (1) и, кроме того, sup 0 j updx = Mu (p) < го при p > 0, B(1+a)p то имеет место оценка j |Du|pdx 6 cp pMu(2p). Bρ C Положив в (6) ф = 2u, получим t jj {uTusp + IDuIp-2DuD(usp)} dxdT = 0, s RN отсюда t JI b«p + ^ur.p +pW'DuD}dxdT= o. s RN Продифференцировав последнее равенство по t и учитывая (7) получим ci j u2sp dx + j |Du|psp dx — p J |Du|p 1sp 1u|Ds| dx 6 0. RN RN RN Опуская положительное слагаемое в левой части, получаем I I Du Ipsp dx 6 p J I Du |p-1s p-1u I DsI dx 6 2-1 |Du |psp dx + cl up I Ds|p dx, RN RN RN RN откуда |Du|pdx 6 cρ-p updx. B Bp B2p Аналогично для решения v уравнения (2) справедливо j |Du|q dx 6 cp-q(Nv(2p)), Bρ где Nv (p) = sup J vq dx. 0 В силу локальной суммируемости функции u имеет место следующая Лемма 2. Если u — решение уравнения (1), то для 0 < s < t 6 T и любых p > 0, c < 1 выполняется t lim / / |uT|x{k < u < ck} dxdT = 0. k→∞ s Bρ Записав равенство (4) для функции v и выбрав £ равным (ф — u)+sp, получим: t 11 {vT(Ф - u)+sp + ।Dv।q-2DvD[(Ф — u)+sp]} dxdT = 0. s RN Используя (6) и (11), приходим к равенству tt j j ^ dtW (Ф — u)+sp + JD(Ф - u)+spj* dxdT = —p j j J (ф — u)+sp-1DsdxdT (12) s RN s RN для любого ф G Xioc(ST), где W = u — v и J = |Du|p 2Du — |Dv|q 2Dv. Представим J в виде J = J0+ J00, где и J0 = |Du|p-2Du - |Dv|p-2Dv J00 = |Dv|p-2Dv - |Dv|q-2Dv. Тогда равенство (12) перепишется так: t t t j j dtW(^ - u)+^p + j j J'D(^ - u)+^p dxdT + j j J"D(^ - u)+?pdxdT s RN s RN s RN tt —p// J0(^ - u)+^p-1D^dxdT - P jI J00(Ф - u)+^p-1Ds dx dT. Полученное равенство (15) является отправным в наших рассуждениях. Имеет место следующая Теорема. Если u и v — слабые решения уравнений (1) и (2) соответственно, w = (u — v)(t) ^ 0 в L|oc(RN) при t ^ 0, если, кроме того, выполнены условия: Mu(p) = sup / up dx < то и Nv(p) = sup / vq dx < то при p> 0, g Bρ Bρ то существуют такие постоянные ag, pg, Tga, а > 1, что для всех 0 < а < ag, p > pg, 0 < t 6 Tg, a > 1 и достаточно малом p - q выполняется оценка 0^+1 / |W|a+1dx Bpx{t} (1 p — 2 tkpρ kp t 1 q —2 -| । 1 । p — q + aq N / \ iff + t kq p kq + t +q + p—>-a-p p p p “) Kuv (p) I g B2P iw i(a-1)a dxdT^ у Здесь kp и kq — постоянные Баренблата уравнений (1) и зависящее от Mu(p) и Nv(р). <1 Положим (2), K (p) — выражение, Un = | u, u 6 n, n, u > n, Wn+ ^ (u — v)+ = 0, w 6 0, w+, w < n, n, w > n. , . В равенстве (15) выберем пробную функцию равной ^ = u 1 +--(W+ + E)aG Xloc(ST)) εε где E G (0,1), a > 0, n G N, ^ G X1oc(St) И Y1oc(St). Тогда из (15) будем иметь t j W(^ — u)+?p dx — j W(^ — u)+?p dx — j j Wdt(^ — u)+^p dxdT RN RN x{s} s RN tt + j j J 'D(^ — u)+Sp dxdT + У У J "D(^ — u)+Sp dx dT tt = —p j j J '(ф — u)+sp—1dxdT — p j j J "D(^ — u)+?pdxdT. Перемножим обе части равенства (18) на ε и перейдем к пределу в полученном равенстве при е ^ 0. По теореме Лебега о мажорируемой сходимости первые два слагаемых левой части равенства (18) стремятся к выражениям j W (Wn+ )a^p dx RN x{t} и j W (W+)a^pdx RN x{s} соответственно. Третье слагаемое равенства (18) после умножения на ε можно сать в виде: перепи- t —-JJ Wdt(Ф — u)+^p dxdT s RN t - a// W(Wn+ + -)а-1^W^X^u 6 | + -W + -)a} ?p dxdT s RN t - $ j W^t(1 - -u)X {- 6 u 6 -(W+ + -)а^ ^p dxdT = L1(-) + L2(-). s RN Последнее слагаемое в силу леммы 2 стремится к нулю при - ^ 0, при фиксированных S и n, действительно: t |L2(-)| 6 е jj |W| s RN t 6P + v s RN t ∂ ∂τu X ^ ” 6 u 6 ~(W+ + -)a | ?p dx dr >Ш - 6 u 6 - (W+ + e)a | ^p dx dr 6τ s RN t +c // s RN N k p ρ p- —N τk _p_ du q ρq- dTX q∂u ∂τ { - 6 u 6 - (W+ + -)a | ^p dx dr x{ - 6 u 6 - + - (Wn+ + e)a} ^p dxdT t -N f f du f 1 cs kppp-2 -Tx\"s s RN 6 u 6 - + - (n + 1)a | ^pdxdT t -N -3- Г f du fl + cs kqpq-2J ] - x|- s RN 6 u 6 - + - (n + 1)a | ^p dx dT, каждое из которых стремится к нулю при - ^ 0. t ЯИ/+ Первое слагаемое равенства (2) стремится к выражению —af J (W+ )a WTn ?p dxdT, sRN которое можно представить в виде t -af f №)"dW-5p dxdT =a- f (W+)a+1(p dx + f (Wn+)a+1s p dx, SRN a + «N Xw a + «N L отсюда и из (19), после предельного перехода при е ^ 0 для первых трех слагаемых равенства (18), получим выражение W+(W+)\p dx RN x{t} - RN x{s} W+(W+)\p dx - [ (W+ )a+1^p dx + "4г a+1 a+1 RN x{t} ■ j (W+)a+1?p dx, RN x{s} которое оценивается снизу выражением ;+T /(W„’ <"1-p dx RNx{t1 — J W +(w+)aspdx. RNx{t1 Докажем, что четвертое слагаемое в равенстве (18) имеет неотрицательный предел при е ^ 0. В самом деле, tt е jj J 'D(^ — u)+Sp dxdT = a^ У J0 DW+ (W+ + e)a-1^px ^u 6 “ + “ (W+ + -)a | dx dT s RN s RN t + j j J0D(1 — eu)spx{| 6 u 6 - + -(W+ + -)aj>dxdT; s RN второе слагаемое данного равенства стремится к 0 при - ^ 0, поскольку функции |Du| и |Dv | — локально ограничены [2, теорема 1]. J0можно представить в виде J0 = |Du|p-2Du — |Dv|p-2Dv = i db{№ + (1 — «v)lP-2D(?u + (1 — ^)v)) d« 0 |D(^u + (1 — ^)v)|p-2de DW +(p - 2) |D(£u + (1 - £)v)|p-4D(£u + (1 - Ov) DWd^ Перемножая обе части последнего равенства на DW скалярно, получим: J 0 DW = / 0 lD«u + (1 - ^)v)|p-2d^DW|2+ (P — 2) У 0 |D(£u + (1 - £)v)|p-2dlDW|2 = (p -1) j № + (1 - ^)v)|p-2 d^DW|2, отсюда следует, что J0DW > 0. Поскольку J0DWn = J0DWx{(x,t) : 0 6 u- v 6 n}, то и J0DW+> 0, следовательно, t lim e J0D(^ - u)+pp dxdT > 0. (22) ■01 J J s RN Оценим пятое слагаемое равенства (18) сверху после умножения на ε: t \ e// s RN J0D(^ - u)+ppdx dT t 6 a S / J00l(W" + E)a-1|DW?+|Ppx( {(M) : u(x,t) 6 E + E (w+ + E)aj> dxdicdT s RN t + У У |J 00|D(1 s RN - uu^ppx ^(x,t) : E 6 u 6 1 + 1(Wn + E)a | dx dτ, последнее слагаемое стремится к 0 при E ^ 0 в силу локальной ограниченности функции |Dv | и |Du|. Что касается первого слагаемого, то его можно оценить так: t а У j |J 00I(W„ + E)a-1|DW+|ppx ^(x,t) : u(x,t) 6 E + E (w+ + u)aj> dxdT s RN tt 6 acУ У |Dv|P(W»+ + E)a-1ppdxdT + асУ j |Du|p(W^ + E)a-1ppdxdT s RN s RN t + ac(p - q) У y(Wn+ + E)a-1ppdxdT s RN t 6 ac^ У T(1+kq)(p q+a)p (p—q^ ) У |Dv|q-a(W+ + E)a-1ppdxdT s RN t + УT-(1+N)app-2 У |Du|p-a(W+ + E)a-1ppdxdT s RN p-a N f p-a ^ +(p - q)(t - s) p p I p Hj j (W+ + £)( V s B(1+a)p 1) p dx dr^ 6 ac(p ^p-P1 j t-(1+N) -q+a) s - B(1+a)p q-q qdx ' B(1+a)p α qq 7+ + e)(a-1)adx I dT t +уT s (1 + N )a2 kp ρp p-α p p p • a 1)adx\ dT ' B(1+a)p ' B(+6)P p-αNp-α +(p - q)(t - s) pp p 2(p-q+ ) P q-2 a q(Nv(4p)) s B(1+a)a αt ■a-1)p dxdr^ q-q (p - q + a)dT 2a s x (j J (Wn+ + £)(a X S B(1+ap) t q αq 1)adxdT j p-α +pp-2(Mu(4p)) p p (Wn+ + e)(a-1) adx α p dτ s - B(1+a)p +(p - q)(t - s) p PN p (j j j (W+ + e)(a 1)adxdT! S B(1+a)p 6 ac(p ' +a-q(Nv(4p))) “ (t1-q-a(1+N) -■+a) s1-q-a (1+ N )(p-q+a)\ s -α q t q q 2 a p a xl (W+ + e)( ) dxdT I + pp-2 (Mu(4p)) p S B(1+a)p Л1— (1+ N )a x It p-a kq s1-p-a<1+N)a) p? H j (W. + E)(a-4a dxdT\ p S B(1+a)p + (p - q)(t - s) ppN p( j j (W+ + e)(a 1)“ dxdT! S B(1+a)p 6 ac ρ 2(p — q+a) q- +a-q+Na (Nv (4p)) q^ (t - s) a (t1-q-a(1+N)(p-q+a) 41-q—a (1+ N )(p-q+a)\ s q-α q +pp—2+a-P(Mu(4p))p^ (t1-p-a(1+N)a 1--— (1+N )a\ p-α kp s p-α p + (p - q)(t - s) PN(>) ([ / (W+ + s)(a S B(1+a)p α pp 1)adxdT I . Из последнего неравенства при выполнении условий 1f1 + N) (p - q + a) > 0 и 1f1 + N) a> 0 q — a V kq) P - a V kq ) (условие (23) достигается за счет малости a и (p — q)), получим t - л sRN J00D(^ — u)+spdx dT / 2(p-q+a) „ N2g 1+ap—q)q—U N Wp-q+a) 6 aclp q—2 q+pq p qt pq q—a( kq)(p q+a) q — a 2a p a— (1 + N )a p — a p — a N/ - \ x(Nv(4p)) q + pp—2t p kp (Mu(4p)) p+ (p — q)t pppp x (Wn + E)(a 1)“ dxdT α p отсюда вытекает, что существуют такие ag > 0 и pg > 0, что при всех 0 < a < ag, p > pg и 0 < t 6 T выполняется неравенство t e j j J00 D(^ — u)+Sp dx dT s RN 1+«(p—qlq_(1+N )(p-q+a) 6 act pg q—a kq Jp N (p — a) p x((Nv (4p)) q"^ + (Mu(4p))p—^ Vj j (W+ + E)(a-1)p dxdT! s B(1+a')p α p +O (!)■ следовательно, при выбранных α, ρ имеет место неравенство lim ■01 t e J j J00D(^ — u)+spdxdT s RN 1+ a;p_qlL (1 + N )(p-q+a) N(p-a) 6 act pq q—a kq p p(p a) x ((N(4p))q^ + (Mu(4p))p^) f j I" sB(1+a)p p αp • a 1)adxdT j , здесь c зависит от p, q, ag, pg,T. Правую часть равенства (18) после умножения на ε можно представить в виде: t —pE J j J (Ф — u)+Sp-1Ds dxdT s RN t = —p j I J (W+ + E)aDsx ^(x,t)u(x,t)6 - + E (w+ + E)aj>dxdT s B(1+a)p t —pE j j J(1 — eu)Dsx ^(x, t) : _ 6 u(x, t) 6 —I— (W+ + E)a| dxdT, s RN откуда будем иметь: t pε I I J(ф — u)+sp 1DsdxdT s RN 6ps B(1+a)p \Du\p-1(Wn+ + -)a\D\ dxdT t +P / / \Dv\q-1(W+ + e)a\D^ \ dxdT + p s RN t +pe j j (\Du\p-1+ \Dv\q-1 t j I (|Du|p-1+ \Dv\q-1) \Ds\ dxdT s B(1+a)p s В(1+ст)р t +cp У j (\DvVq-1(W+ + -)a) dxdT + cp s B(1+a)p t )u\D?\ dxdT 6 — f f \Du\p-1(W+ + -)adxdT P s B(1+a)p t I I (\Du\p-1+ \Dv\q-1) dxdT s B(1+ct)p t +O t p-pα J J (\Du\p-1(W+ + e))P-PadxdA s B(1+ct)p x j j (W+ + -)(a1)P dxdT s B(1+ct)p t αp t p-pα + M j (\Dv\q-1 (W+ + -))adxdA s B(1+ct)p x j j (W+ + -)(a1)P dxdT s B(1+a)p p -1 kp _kz_\ /1\ I + c ( tkppp-2+1kqp q-2 I + O ( - I . Из последнего неравенства после предельного перехода получим lim ■01 t p-j j J(ф — u)+Zp-1DZdx dT s RN + p-a (\Dv\q-1(W+)) ~ dxdT x a/p (w+ )(a-1)adxdT ) t -p 6 p (j j (\Du\p-1(W+)) p-pa dxdT\ P L S B(1+a)p p-a p I / 1 P — 2 + cUkpp kp 1 q —2 + t kq p kq Оценим выражение стоящее в квадратных скобках соотношения (25): t s B(1+a)p t p-a p-a p (\Du\p(Wn+)) pdxdT j + 1 / t t s B(1+ct)p updx dτ p-a p-a p (\Dv\q-1(W+))~ dxdT p (p—yp \Du\p—a—1dxdT - a —1 p p dx dτ - ■ a —1 p t \ p updx dτ t p (q—1)p \ |Dv |p—a—1dxdT - — a —1p 6c t \ p updx dτ s B(1+a)p s B(1+a)p s B(1+a)p t +c X s t -(1+ N. ) 2ap_ _____4ap_____ T ' kp'p — a — 1p (p —2)(p —a —1) p /( p —2a —1 \ |Du| p—a—1dxdT B(1+a)p •—a —1p s B(1+a)p t 4a। aN 6 cpp—2p \p updx dτ \p updx dτ t s B(1+a)p |Dv|qdx dT j q—1 q p-q-αq t q(p—a—1)p Np-q-αq i q(p—a—1) t s B(1+a)p s T(1+Np)p—a—1f у (|Du|pdx В(1+ст)р p p —2a -1 -α- dτ •—a —1 p t p-q-αq - +ct q(p-a-i) p Np-q-αq ( q(p — a — 1) \p updx dτ t s B(1+a)p s B(1+a)p |Dv|qdx dT j q-1 q 14-1—( 1-^N-1 2ap 4a। aN p —2a 6 ct1+p(1+kp ) p —a —1p p—2 + — -(P-2a-1)(Mu(4p)) ~ 1+11 + +t1+pp+ p-q-αq q(p—a—1)p p—q—aq 1 q—1 \ . q(p—a—1)(Mu(4p))p (Nv(4p)) q 1. получим оценку ■о t pe j j J(ф — u)+Zp-1DZdxdT s RN / i p—2 i q—2 6 cltkp p kp + tkq p kq +1 1+11 + p—q—aq : p q'q(p—a—1) -1 x(Mu(4p)) p (Mu(4p))p(Nv(4p)) q где c зависит от p, q, ао, N, T, pо• Итак, из (18) на / i p—2 6 c tkpρ kp t s B(1+a)p a/p •a-1)a dx dT j a + 1 j (Wn+)a+1dx — Bpx{t} j W+(Wn+)a dx Bpx{s} — q—2 1+1 + t kq p kq + t pp 1 + p—q q'q(p—a - ^L N (p-a) 1)p p 7 q-α p-α ((Nv (4p)) ” (Mu(4p)) —) t p—2a 1 q—1 +(Mu(4p)) — + (Mu (4p)) p (Nv (4p)) ~ a/p a-1)a dxdT j . Переходя к пределу при s ^ 0 в последнем неравенстве, получим оценку 1 a + 1 J (Wn+)a+1 ( 1 P-2 dx 6 c tkpρkp 1 q— 2 + tkq p kq 1+ ii + pq -.q N (p-a) + t p q q(p—a—1) p p w ' B(1+a)p q — a p — a p — 2a 1 q— 1 x((Nv (4p)) q (Mu(4p)) ~ +(Mu (4p)) “V + (Mu(4p)) p (Nv (4p)) "V) x a/p (W+ )(a-1)a dxdT | Меняя местами u и v , и записав (27) в этом случае, мы приходим к оценке a + 1 7 1 ( -1 p—2 -1 q—2 ■ IW+Г1dx 6 c tkpP kp + tkqP kq Bpx{t} 1+ ii + p—q—aq N (p-a) + t p q q(p—a—1) p pXI ' xKuv (p) α/p |W+ |(a-1)a dxdT , где q — a p — a p — 2a 1 q — 1 Kuv(p) = (Nv(4p))“ (Mu(4p))"V + (Mu(4p))“V +(Mu(4p))p(Nv(4p))~. Окончательно для 0 < a < ao, p > po, 0 < t 6 T, после предельного перехода в неравенстве (28) будем иметь / ( -I. p—2 1 I 1 — 1 I p — q+aq N ( a+1 |W |a+1dx 6 cltkpp kp + t+p q + q(p—a—1)p pp KUuy (p) Bpx{x} t x 0 B2p (a 1) p dx dT^ . B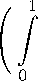
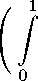
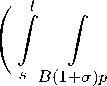
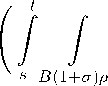
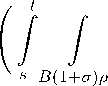
+
)
Отсюда при соответствующем подборе ао и pо из (25) при всех 0 < а < ао, и 0 < t 6 T
lim
,
основании (21), (22), (24), (26) будем иметь
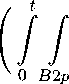
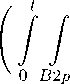
Список литературы Локальные свойства решений задачи коши для квазилинейного параболического уравнения второго порядка
- Benedetto E. D., Herrero M. A. Non-negative Solutions of the Evolution p-Laplacian Equation. Initial Traces and Cauchy Problem when 1Trans. Amer. Math. Soc.-1989.-V. 314.-P. 225-290.
- Benedetto E. D., Herrero M. A. On the Cauchy problem and initial traces for a degenerate parabolic equation//AMS.-1989.-V. 314, №1.-61 p.
- Shelepov V. Yu., Alexander F., Tedeev A. F. On an inequality for solutions of elliptic equations and its application in the theory of boundary properties//Soviet Math. Dokl.-1991.-V. 42, № 3.-P. 732-736.
- Тедеев Ал. Ф., Шелепов В. Ю. Об L_p-граничных решениях эллиптических уравнениях в негладких пространственных областях//Нелинейные граничные задачи.-Донецк: АНУ ИПММ.-1992.-№4.-С. 52-100
- Шелепов В. Ю. О граничных свойствах решений эллиптических уравнений в многомерных областях, представимых с помощью разности выпуклых функций//Мат. сб.-1987.-Т. 133(175), №4.-С. 446-468.


