Lorentz Force, Ampere Force and Momentum Conservation Law Quantitative. Analysis and Corollaries

It is known that Ampere force contradicts the Third Newton Law, but it does not contradict the more general Law of Momentum Conservation, as the electromagnetic field has a momentum. It is important to note that a stationary electromagnetic field can also have a momentum and therefore the Ampere force does not contradict law of conservation of momentum, also in the case when it occurs in conjunction with a permanent magnetic field. From this it follows that the Ampere force must be balanced by the flow of electromagnetic momentum. However, as far as the author knows, a quantitative comparison of the Ampere force with the flow of electromagnetic momentum does not exist. Therefore this comparison will be discussed below. Here we shall also define some parameters, and taking them into account we shall show that the Lorentz force and Ampere force can be regarded as corollaries of the existence of electromagnetic momentum and the law of momentum conservation.

For an electromagnetic field let us denote:

W - the energy density (scalar), kg·m^-1·s^-2,

S - the energy flow density (vector), kg·s^-3, p - the momentum density (scalar), kg·m^-2·s^-1, f - the momentum flow density (vector), kg·m^-1·s^-2

• V - the electromagnetic field volume (scalar), m³,

The fig. 1 shows conductor carrying current I and length of L that is located in a magnetic field with induction B and is moving at the speed v under the action of the Ampere force F . Vectors of the intensity E of the current-creating electric field, and of the induction B - are mutually perpendicular.

Therefore there appears a flow of electromagnetic energy with a density S , shown in the fig. 1 by circles. It may be presented in the form of two spheres, united in the body of conductor and penetrating the conductor in the vertical direction. This flow is equivalent to the flow of an electromagnetic momentum f .

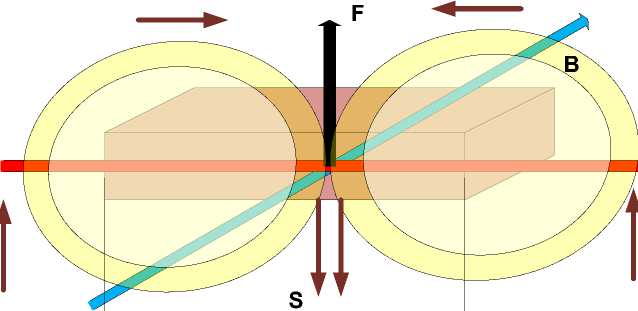
B

F

S

I

L

Fig. 1.

It is known [1, 2], that

If = W.(1)

S = W • c,(2)

P = W/c, p = S/c2,(3)

f = p • c, f = S/c.(4)

The integral of the density by volume will be denoted as

AV =J A • dV .(4а)

V

The energy flow S_V may exist also in a stationary electromagnetic field

• [3] . Therefore the momentum flow f_V exists also in a stationary electromagnetic field created by direct current and permanent magnetic field.

The law of momentum conservation for a device interacting with electromagnetic field can be written in a following form [3]:

• -"I ( J ) =-d ( pv ) + fi' .                           (5)

dt       о t where

J – mechanical momentum of the device,

V - the volume of device; volume in which the electromagnetic momentum interacts with the device (the summary momentum flow in all volume of the field is equal to zero).

It is known that the force acting on the device is

F = —d(J )

d t

Consequently,

F   V'(^: )⁺ fv У

(dt

Combining (7) and (3, 4), we get:

F = f-f SV-) + SV-(dt (c2)

Thus, if the device is in the flow of electromagnetic energy S_V , then it is influenced by a force (8), depending only on the flow of electromagnetic energy S_V . This force exists also for a permanent flow S_V , and then

F = SV

c

.

In this case, if the flow of electromagnetic energy electromagnetic energy flux is distributed in the material with relative permittivity ε and permeability µ , then in the formulas (8, 9) the light speed c in vacuum should be replaced by the light speed in material

c

C s =^                                  (10)

εµ

Let us consider the case (shown on the fig. 1), when vector of permittivity E and permeability H are perpendicular. Then

S = EH                                         (11)

Let also the field in the device is uniform and is concentrated in the

volume V . Then from (8, 10, 11) we get

F = V f^f EHM ) ₊ EHj⁵' ^d t V c² ) c ^

If, besides that, the field is permanent, then

F=VEH 4^i. c

3. The Lorentz Force

Let us consider the magnetic Lorentz force, acting on a body with charge q , moving with speed v perpendicularly to the vector of magnetic

inductivity B :

^fl = qvB •

We shall neglect the intrinsic magnetic induction field of a moving charge (compared with the induction of an external magnetic field) and its own electromagnetic momentum moving charge. Then we have to accept that the force (14) is caused by the flow momentum of electromagnetic field that penetrates the body of the charge. Thus from (13, 14), we obtain:

FL=VEH 45* Lc

where V – is the body volume. From this we get:

EH εµ qvB = V------ c

or, for B = M o ^ H ,

qvc =

VE ε/µ µo

Consequently, inside the body there should be electric field intensity directed along the velocity, and equal to

E = qvc—

V ε/µ

Let us note that — c—o = —o- « 377

ε o and

E

£ = qvc— µV

377 ^q v . V

Consequently, inside a charged body, moving in a magnetic field and being under the influence of Lorentz force, there exists an intensity of electric field proportional to the movement speed .

The example with an Electron

It has a charge q_o = 1.6 • 10 ^{— 19} , classical radius r_o = 2.8•Ю - ¹⁵ , a

4 πr ³

— -

45 . Also

volume corresponding to this radius, V_o = —3— = 92 • 10

E — « 7 • 1026 • v . One may also say that on the diameter of the µ electron along the speed direction, there exists a potentials difference - a voltage Uo = 2Eoro « 4 • 1012 • v../— . Considering the ε arguments of Feynman [3] on the internal forces of the electron, restraining the electron charges on the surface of the sphere, we can see that this voltage is the force which "pulls" lagging charges to their place on the sphere when they move under the action of the Lorentz force

4.    The Ampere Force

Let us consider the Ampere force acting on a conductor with current I , дmoving with speed v perpendicularly to the vector of magnetic induction B :

FA = IBL.

If this force is caused by the flow of the momentum of electromagnetic field permeating the conductor, then

F A = ^НЦ^ ,                          (22)

c where V –is the conductor’s volume. From this we find:

IBL = vEHRt

c or, forB = totH ,

EH εµ IHLp o p = V ------•		(24)
	c
Therefore, the intensity of electric field in this case will be
E = ILct o V ε / µ		(24а)
If s is the section area	, L - the conductor length, then
V = sL .		(25)
If the voltage on the conductor is permanent and equal to U , then
E = U / L		(26)
If the specific resistance of the conductor is equal to ρ , then
U = IpL/s	= jpL	(27)
and
E = jp .		(28)
Then
jscµ jp =		(29)
sε	/ µ
or
	2
e = Cto'	t .	(30)
I p )

Thus, the permittivity of the conductor with current depends only on µ and ρ .

For example, for t = 1, p = 2 - 10 - 6 (om*m) we find that e « 7 - IO¹⁶ .

For verification let us substitute (30) into (22) or into (13), we shall get

F A = VEH    =      .                           (31)

ρρ and further, taking into account (28), we get (21). Similarly, substituting (30, 28) into (12), we get

Fa = V 2 Л EH ' MoM' 2 ^ +EH 4^1 = V ( MoM 1 EH + EH ^o^- dt V V C V p ) 7 c 7 V cp dt v p 7 p7 or

Fa = L^dAl®^ IBL.

cp о t

Hence, the Ampere force must depend also on the speed of current change or on magnetic induction. These changes may be caused by current change of by the change of current position relative to the field. Practically such dependence can be detected only for very high frequency

(due to the coefficient Mo- « 4 - 10 ¹⁵ ).

c

5.    Discussion

From the above said it follows that the Ampere force may be considered as a corollary of the existence of electromagnetic momentum flow and of the momentum conservation law. But in this case it should also be assumed that the permittivity of the current-carrying conductor depends on µ and ρ according to (30). In this case the dependence of the Ampere force on the speed of current change and/or magnetic induction can be revealed.

Combining (20) and (30), we find

E^ = qvctio.

V p 7 V or

e=qpv V

Qualitatively, this effect can be explained by the fact that the free electrons "lag" from the body and accumulate in the "tail" of accelerating body - a phenomenon considered by Feynman for accelerating electron [3]. Electrical resistance of the material slows uniform charge distribution. For this consumes energy. Consequently, the motion of the charged body at a constant speed occurs with the expenditure of energy for thermal losses. This ensures constancy of the energy of the electric field inside a charged body.

Thus, the the Lorentz force can be regarded as a corollary of the existence of electromagnetic momentum flow and of the momentum conservation law. But in this case it should also be assumed that inside the charged moving body exists the intensity of electric field of the form (34), proportional to the movement speed.