Lp-Lq-оценки для операторов типа потенциала с осциллирующими ядрами

В работе получены L p — Lq-оценки для операторов типа потенциала

a(t‘)b(|t|) ei^ ,         .

(^R ^Kx) = J —у—_a— T⁽x ^— t) dt

(i)

Rn где 0 < Re a < n, a(t’) (t‘ = t/|t|) — однородная нулевой степени функция, бесконечно дифференцируемая в Rn \ {0}, удовлетворятотцая условию a(t’) ^ 0, t‘ Е Sn-1.

Предполагается также, что радиальная функция b(r) принадлежит классу C^m,Y (R+) гёльдеровских функций (см. §2).

В работе описаны выпуклые множества (1/p, 1/q)-nnocKOCTH, для точек которых оператор R^a ограни чей из Lp в Lq, и указаны области, где этот оператор не ограничен (см. теорему 1.1). В некоторых случаях доказана точность полученных оценок (см. замечание 1.1). В частности, получены необходимые и достаточное условия ограниченности оператора, (1) в Lp.

В настоящее время имеется ряд работ по Lp — Lq-оценкам для операторов свертки с осциллирующими ядрами, в частности, для операторов Бохнера. — Висса, и акустических потенциалов, возникающих в различных задачах анализа, и математической физики (см. книги [1] и [2], а. также работы [3-6, 7-9]). Во всех упомянутых работах, кроме [3] и [7], рассматривались ядра, содержащие только радиальную характеристику b(r), которая стабилизируется на. бесконечности как гёльдеровская функция. Благодаря этому свойству получение оценок для указанных операторов сводилось к случаю оператора, с характеристикой b(r) = 1. Подобное сведение в принципе невозможно, когда ядро оператора (1) содержит однородную характеристику a(t’).

В работе [3] были получены оценки для потенциала (1) в случае b(|t|) = 1 и (п—1)/2 < Re а < п. Однако, использованный в ней метод, основанный на представлении оператора Ra через оператор Бохнера — Висса и некоторый оператор, близкий к акустическому потенциалу, не работает при Re а ^ (п — 1)/2.

В работе [7] развивается новый метод, основанный на. получении специальных представлений для символа оператора (1) (в случае b(|t|) = 1) с последующим применением техники Фурье-мультипликаторов, вырождающихся или имеющих особенности на. единичной сфере в Rn. Этот метод позволяет получить Lp — Lq-оценки для потенциала (1) в случае b(|t|) = 1 при любых значениях а. удовлетворялзпщх условию 0 < Re а < п.

• 1.    Формулировка основного результата

В работе использованы следующие обозначения: (A, B,...,K ) — открытый много угольник в R² с вершина!ш в точках A, B,..., K: [ A, B,..., K ] — его 'замыкание.

Перо; L (A) обоз:зачим L-характерпстпку оператора A. т. е. множество всех точек (1/p, 1/д)-плоскости (1 ^ p ^ q ^ то) таких. чт<> оператор A ограничен из Lp в Lq.

Пусть 0 < Re а < п. Введем в рассмотретше следующие точки (1/p, 1/д)-плоскости:

Re а\        /Re а \

^A = (*-^{1 —}—/ A = ( — т

C =

-

2 Re а 3 п — 1 ^, 2

-

2 Re а п —1

/ 2 Re а

\ п — 1

1 2 Re а 1

2 ^, п — 1 — 2

E = И, ⁰⁾, F =(| , 2) ,

G =

G ^′

-(

Re а n

( п — Re а )( п — п ( п + 3)

H =

1—

Re а

, ¹ n

Re а

-

n

,

H ^′

-(

Re а n

Re а n

,

О = (1 , 1) ,   О’ = (0 , 0) ,

K =

/ 2(Re а + 1)

V п + 1

-

1 , 1) , K ‘ = Н , 3

2 , 2 ,                  2 , 2

-

2(Re а +

п +1

B =

—

(n — 1)(n — Re а) n(n + 1)     ’

Re а

)■  B‘=(

Re а

(n — 1)(n — Re а) n(n + 1)

.

n

n

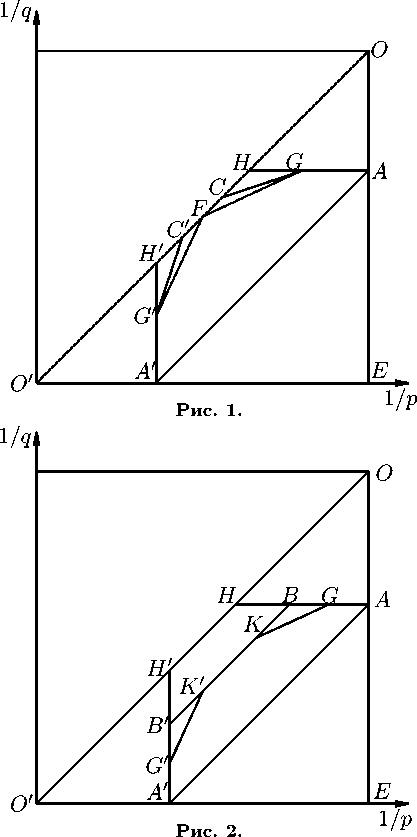
Нам понадобятся также следующие множества на (1/p, 1/q)-nnocKOCTH (см. рис. 1 и 2 для случаев 0 < Re а ^ n^-1 и n--¹< Re а < n соответственно):

[A‘,H‘,H, A, E] \ ([A‘,H‘] U [A, H]),

(A’, G, C\ C, G, A, E) U (A, E] U (A’, E) U (C‘, C ),

(A’, G , F, G, A, E) U (A, E] U (A’, E) U { F } ,

0 < Re а < nn—1). n(n—1)              n— ¹

2(n+1) < ^{Re а} < 2 , Re а = n^{- 1}, Im а = 0,

L1(а,n) = (A,G,F,G,A,E^ U (A, E] U (A,E),

а =

n—1

2 ,

(A, G, K', K, G, A, E) U (A, E] U (A, E) U [K‘, K ], (A, B , B, A, E) U (A, E] U (A, E),

n^-1< Re а < 2

2,

_ (A, B , B, A, E) U (A, E] U (A, E) U (B‘, B ),

n2 < Re а < n, Im а = 0, n2 <  а < n,

L2(а, n) = [O, A, A, O’] \ ( { A’ } U { A } ).

Основным результатом статьи является следующая теорема.

Теорема 1.1. Пусть 0 < Re а < n.

• I.    Справедливо вложение

L (R^a) D L i(a,n) П L 2(a,n).                          (2)

• II.    Множество L(R^a) не содержит точек лежащих:

• 1)    на отрезке [A, H ] и выше iтого, если a(a) = 0. ст G Sn^-1:

• 2)    па отрезке [A‘, H ‘] и левее пего при том же у словпп па характеристику а(ст). что и в п. 1);

• 3)    на отрезке [O’, О], ее-ли а = (n — 1)/2г

• 4)    ниже- прямой A A. а также толки A ii A.

• 2.    Вспомогательные сведения и утверждения

Замечание 1.1. При 0 < Re а С П^Д) ^и n/2 С а < n полученные оценки являются точными. А именно,

L (R^a) = [A‘, H‘, H, A] \ ([A‘, H ‘] U [A, H ]), 0 < Re а С nn — ¹,

2(n + 1)

L (R^a) = (A’, B‘, B, A, E) U (A, E] U (A’, E) U (B‘, B ), n/2 С а <  n.

В частности, для таких а получено необходимое и достаточное условие ограниченности оператора (1) в Lp. Именно, этот oneратор ограничен в Lp тогда и только тогда, когда n/(n — Re а) < p < n/ Re а.

Следуя [1], будем говорить, что функция f(r) принадлежит классу C^m;Y (R.), m = 0,1, 2,... , и 0 С Y С m, если выполнены следующие условия:

• i)    функция f (r) G C ^m(R + \ { 0 }):

• ii)    функция f *(r) = f ( Г ) имеет в точке r = 0 производпые до m-ro порядка включи тельно;

• iii)    в точке r = 0 yin<тщя f(r) имеет непрерывные npoirвводные до порядка [y] включительно, и справедлива оценка

|f(p)(r)| С rY-p, при r ^ 0. p = [y] + 1,..., m.

В случае y = m имеем C^т;т(Г^+ . ) = C^m(R .).

Лемма 2.1 [1]. Пусть f (r) G Cm,Y(R.), m ^ 1. Тогда справедливо разложение m-1

f (r)=kg ,,+;;•).. .■+fm(r), где ak = -1 f»(k)(0) = (—^ f(1+ r2)3/2 df) f (r)!,^,(3)

k!             k!          r dr fm^r^Vm — 1)!(ll+ r2)m/2 i^ — uV"-1 f^ ^Д!^) du^

Злесь f(t) = f (^ ^-p²- ) •

Кроме того, справедлива оценка

|fm ( r ) | <  c (1+ Г 2) m ,

для некоторого c >  0.

Далее, рассмотрим потенциал

′ i|t|

№)(x) =  4^-0- v(x - t) dt,

| t |

Rn где 0 < Re a < n, a(t'), t' = t/|t|, — однородная нулевой степени функция, бесконечно дифференцируемая в Rn \ {0}. удовлетворялипая условию a(t') Д 0. t' Е Sn—.

В работе доказана следующая

Теорема 2.1 [7]. Пусть 0 < Re a < n.

• I.    Справедливо вложение

L(R^ D Li( a,n ) П L2( a,n ) .

• II.    Множество L(Ra не содержит точек, лежащих:

• 1)    на отрезке [A,H ] и выше iтого, если а ( ст ) = 0. ст Е S^n-1:

• 2)    на отрезке [ A', H ‘ ] и левее него при том же у словии па характеристику а(ст'). что и в п. 1):

• 3)    на отрезке [ O', О ], ее-ли a = ( n — 1) /2r

• 4)    ниже- прямой A A. а также толки A ii A.

• 3.    Доказательство основного результата

Имеем

( RW^ ( У + У } ^{b | l}t | tyt '. a ^{e i | t |} * — t ) dt Д ( M^a'⁰v )( x ) + ( M“'“^Ц ) . |t|<1      |t|>1

Отметим, что ядро m^a,°(t) оператора M^a,0 принадлежит Li. Следовательно, опера тор M ^a,° ограшnieii в Lp. 1 ^ p ^ то.

С другой стороны, для оператора M ^а,° справедлива теорема Соболева. Отсюда следует, что

L(M ^a° ) D [ О', О, A, A' ] \ ( {A'} U {A} ) .                        (6)

Рассуждая так же, как и в статье [6], заключаем, что L(M ^а,°) не содержит точек мно жества [ A', A, E ] \ ( A', A).

Рассмотрим оператор Mа,“. В силу леммы 2.1 имеем m-1

b(r)= kE° д+Д2дТ2 + bm(r), где коэффициенты а^ и функция bm(r) определяются равенствами (3) и (4) соответственно.

Разложив функцию (1 + r2) k/2 по формуле Тейлора с остаточным членом в интегральной форме, будем иметь m—1           l-1 / к ь«=Е ak р+Е 7 r2s+Ri (?) + мн, k=0     \ s=1 '   7            V 7 /

где r > 1. m > 1. (n) =

Ri (4)= n, /(1 - u)^l— 1 ((1 + 4)-^k/2)^(l) du, \r² /     r²l (l — 1)!                        r²

здесь l = [a] + 1.

С учетом (7) получаем

(M ^a^)(x) = ao(R^)(x) + mE ak№-^k)(x)

k =1

+ E E Г_skК (Ra^-k—2s)(x) + E ak к^-k ^m + (si^v k =0 s =1                          k =0

Здесь

(t. .— к_V)(x)= [ ■                    — t)

a                               | t | n— ( a—k )

|t|> 1

Г a(H)bm(ltl)ei^tt

^{( S} a W^{( x )} = J       | t | n—_a---- V^{(x —} t) ^dt-

|t|> 1

Заметим, что для операторов R^a и R^{a к 2s} (0 7 k 7 m — 1,1 7 s 7 l — 1) справедлива теорема 2.1. Из указанной теоремы вытекают вложения

L(Ra D L1 (a,n) П L₂ (a,n);                        (8)

L(R^^-28) D L1 (a,n) П L2 (a,n).                      (9)

Кроме того, из утверждений п. II теоремы 2.1 вытекает, что множество L (R^) не содержит точек, лежащих:

• 1)    на отрезке [A, H] и выше izero, если a(a) = 0. а Е S^n—1:

• 2)    iza отрезке [ A‘,H‘ ] ii левее пего при том же уе.товпп iza характеристику а(а). что и в п. 1);

• 3)    па отрезке [ О’, О ], еели а = ( n — 1) /2:

• 4)    ниже прямой A’A, а также точки A’ и A.

Поскольку ядра операторов Ta-^k, 0 7 k 7 m — 1, принадлежат L 1, то, с одной стороны, операторы Ta^—k ограничены в Lp, 1 7 p <  то, а с другой — в L^.

Интерполируя, получаем

L(T“-^k ) = [O‘,O,E], 0 7 k 7 m — 1.                     (Ю)

Далее, с учетом (5) имеем

L (Sa = [O',O,E\-                             (11)

Из условий (6), (8)—(11) вытекает утверждение теоремы 1.1.