Магистральное решение в дискретной модели регионального развития

В настоящее время многие прикладные задачи оптимального управления из различных областей оказываются вырожденными, имеющими точные или приближенные магистральные решения. Магистральное решение находится в результате исследования задачи меньшего порядка, получающейся из исходной выявлением и исключением пассивных дифференциальных связей или дискретных цепочек.

В статье определяется магистральное решение задачи оптимизации стратегии развития региона на основе дискретной эколого-экономической модели с учетом инновационного фактора.

1. Схема поиска магистральных решений

В работах [1,2,3] рассматривается эколого-экономическая модель оптимизации стратегии развития региона. В дискретной форме модель представляет собой управляемую систему с неограниченным линейным управлением вида

x (t + 1) = g ( t , x ( t ), u ) + h ( t ) v ,   t e T = { t i ,t I + 1,

...

, t F } , u e U ( t , x ), v e R^k ,

здесь k <  n , h - n x k - матрица, имеющая ранг k .

Будем рассматривать задачу оптимального управления в стандартной форме как задачу (D, I)

поиска минимизирующей последовательности функционала I = F ( t, , x ( t I ), t_F , x ( t_F )) на множестве

Dрешений системы (1), удовлетворяющем дополнительным ограничениям и граничным условиям x e X(t) c Rn,(t,,x(t,), tF, x(tF)) e Г.

При некоторых дополнительных предположениях система (1) может быть преобразована в эквивалентную ей с точки зрения поставленной задачи систему меньшего порядка. Для этого строится вспомогательная система, называемая производной посредством линейного преобразования y = Л ( t ) x , где Л (1) задается так, что Л (1 + 1) h ( t ) = 0. Производная система имеет вид

y ( t + 1) = Л ( t + 1) g ( t , x , u ), u e U ( t , x ), x e { x : y = Л ( t ) x }.

По построению любое решение исходной системы x(t) удовлетворяет производной, но не наобо- рот, причем производная система допускает разрывы x(t) , которая играет роль управляющей функции наряду с u(t) ) со значениями на множестве Q(t, y) . Иными словами, множество решений производной системы шире, чем исходной.

Тем не менее исходная и производная системы эквивалентны в том смысле, что любая траектория производной системы в пространстве (t, x) аппроксимируется последовательностью траекторий ис- ходной xs (t) почти всюду на заданном отрезке [tI,tF] .

Перейдя к новым переменным y = n(t, x), z = Z(t, x) (по взаимно однозначному преобразованию как показано), исходная система (1) имеет вид y (t +1) = gy (t, y, z, u),

Z (t +1) = gz (t, y, z, u ) + hz (t, y, z) v, а производная система в новых переменных получается исключением уравнения (5).

Решение производной системы в пространстве (t, x), x(t) рассматривается как обобщенное реше- ние исходной системы, называемое импульсным режимом. Каждый непрерывный участок x(t) назы- вается магистралью.

Заменим дискретную цепочку в (1) соответствующей производной системой. Тем самым множество D заменяется некоторым более широким множеством E , поскольку при этом происходит исключение цепочки (5). Соответствующую задачу о минимуме рассматриваемого функционала I на E назовем производной задачей.

Из того, что D c E и из аппроксимируемости любого элемента из E последовательностью из D следует, что в (2) имеет место равенство, исходная задача эквивалентна производной и ее решение является магистральным.

Е.В. Дрыганова. Магистральное решение в дискретной модели регионального развития

Таким образом, для рассматриваемого класса дискретных управляемых систем с неограниченным линейным управлением она заведомо вырождена: имеется пассивная дискретная цепочка, выявленная в ходе преобразований и которая как раз и исключается. В итоге исходная задача заменяется точно или приближенно производной задачей, имеющей меньший порядок, что означает упрощение исходной. В свою очередь, если производная задача вырождена, то она вновь может быть преобразована к производной задаче и т.д. до тех пор, пока такая процедура возможна.

2. Пример

Рассматривается дискретная версия модели региона с инновационным сектором, подробно описанная в [1]. Временной шаг равен одному году.

k(t +1) = k(t) + u - 5k(t),(6)

r(t +1) = r(t) + r + N(r(t) - r) - Cy + z, 0 < y < g(k, L),(7)

5(t +1) = 5(t) + (d + Hu)(5 - 5(t)),  5(0) = 0,(8)

k

П(t +1) = П(t) + (1 - A)y - Bu - Azz - Adkd - s(r - r)2.(9)

Здесь y, z, d - выпуск продукции, темп активного природовосстановления и темп активных инноваций; c - конечное потребление; k, g(k,L), u,5 - соответственно основные фонды, мощность, инвестиции и темп амортизации; L- население (предполагается, что трудовые ресурсы, от которых фактически зависит мощность, пропорциональны населению); A, Az, Ad - коэффициенты прямых затрат в производственном, природовосстановительном и инновационном секторах; B - коэффициент фондообразующих затрат; r - индекс состояния природной среды и ресурсов; r(t) - заданная функция (опорная), например, получаемая из статистического прогноза; N, C - коэффициенты самовосстановления и прямого воздействия экономики на природную подсистему; 5 - инновационный индекс, имеющий смысл среднего процента инновационных изменений некоторой группы параметров (в данном случае A и C) относительно их значений в начальный момент времени; 5(t) - значение 5 , соответствующее мировому уровню в данный момент; H - коэффициент, отражающий влияние инвестиций, связанных с расширением производства; П имеет смысл дохода за вычетом штрафа s(r) за экологические нарушения на заданном временном интервале.

Предполагается, что g(k,L) - классическая вогнутая производственная функция, а коэффициент прямых затрат A может быть снижен за счет инноваций вместе с другим важным параметром – коэффициентом C, т.е. будем рассматривать эти коэффициенты как функции A(5) и C(5) с указанными свойствами. Учитывается удорожание инвестиций с ростом их «инновационности» посредством возрастающей зависимости B(H) . Остальные коэффициенты для простоты принимаются кон- стантами.

Предполагается также, что природо-восстановительная и текущая инновационная деятельность ведется на существующих мощностях и требует лишь дополнительных текущих затрат. При этом переменные y , z , u и d рассматриваются как управления, подчиненные ограничениям:

k >  0, г >  0,0 <  y <  g ( k , L ), d >  0.

В [1,2] при идеализирующих допущениях находится магистральное решение, не зависящее непо- средственно от граничных условий. Опишем кратко процедуру его нахождения.

Для удобства 5 заменяется новой переменной y = H ln k + ln( 5 - 5 ), тем самым упрощая связь (8):

Y ( t + 1) = y ( t ) - ( d + H5 ), y (0) = H In k 0 + In 5 .

Нетрудно видеть, что в силу заданных дифференциальных связей и ограничений получаются есте- ственные верхняя ()u и нижняя ()l границы изменений искомых функций k(t), r(t) и γ(t) :

^ku = ^kF >  ^k ( t ) >  ^kl = ^k 0 , r u = r F >  r ( t ) >  r l = r 0 , Y u = Y 0 ^{- H 5 t} >  Y t >  Y l = Y f ^{- H 5 (} t ^- t F ^).

В соответствии с теорией вырожденных задач управления u , z принимаются неограниченными и производится двукратный переход к эквивалентной производной задаче первого порядка о максимуме функционала П посредством преобразований x = П + p ( A^z r + Bk ), § = x - pA d k ₀ y .

Коэффициенты A и C задаются следующим образом:

A = (1 - a 9 )A₀, C = (1 - (1 - a)9 ) C ₀,0 <  a <  1,

Положим g ( k , L ) = mk ^a LA (это известная функция Кобба-Дугласа), L = const (при этом

g(k, L) = qka ), s (r) = s (r - r)2, где s - коэффициент штрафа. С учетом этих предположений и при естественном условии рентабельности экономики дело сводится к максимизации суммы tF-1                                                                                              _

П = ^ ((Л(r) +ц(r)9)qka - ^(r)eYqka-H - B5k + AN(r - r) - s(r - r)2) - tI

- B ( k F - k 0 ) - A ( r F - Г о ) + A d k o ( / f - Y 0 + H5t F ),

где Д г ) = 1 - b ( r )A o - AC ₀, ц(r ) = max(b(r)A₀,A ^z C_o).

Последняя сводится к серии конечномерных задач при каждом t . Из решения (9) находится магистраль, по которой определяется верхняя граница функционала.

Расчеты проводились для условного Байкальского региона при следующих исходных данных:

t_F = 20, A 0 =0.5, 5 =0.05, C ₀ = 0,7 - 10 — ⁵ B =1, A =8000, k ₀=400, k F =800, r ₀=0.8, r_F = 0.9, Г =1,

N = - 0.01, q =12, a =0.7, s =1200, H =0.5, A d =1, b 1 = 0, b ₂ = 0.

Для решения производной задачи применялся метод проекции градиента.

Приведем результаты вычислительных экспериментов, в которых исследовалась зависимость зна-

10 ^{- 4}

. В таблице 1 приведе-

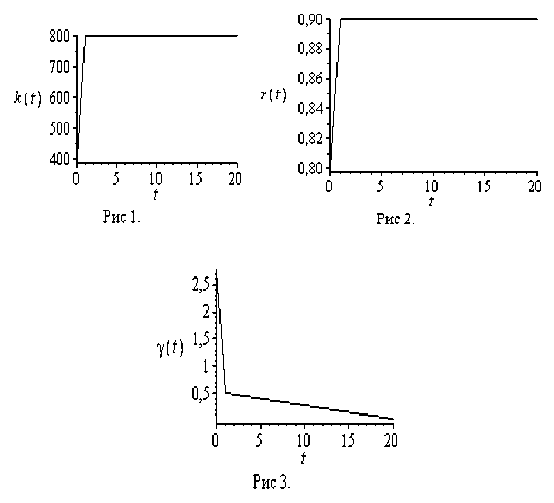
Л.М. Макшанова, Н.З. Злыгостева, Д.Ц. Митупова, М.С. Содномова. Оптимизация ТКС по критерию максимума рентабельности предоставления инфотелекоммуникационных услуг провайдера

Заключение

В работе [3] магистральное решение в задаче оптимизации стратегии развития на примере Байкальского региона находится на основе непрерывной модели. При этом значение функционала П_F ≈ 14694,542. В данной работе в ходе проведенных вычислительных экспериментов показано, что предлагаемый подход позволяет найти сравнимое по точности приближенное решение. При этом трудоемкость рассматриваемого метода существенно меньше, поскольку вычисление решения производится в конечном числе точек. Результирующие значения целевого функционала, как и следовало ожидать, при уменьшении шага дискретизации приближаются к расчетному значению на непрерывной модели и при Δ t <  10 ^{- 2} целевой функционал перестает практически меняться. Таким образом, предлагаемый подход может быть достаточно эффективен для расчета приближенно-оптимальных (магистральных) решений задач рассматриваемого класса.

Найденное магистральное решение может служить хорошим начальным приближением для итерационных процессов, используемых для дальнейшего уточнения оптимального решения в модели оптимизации стратегии развития на примере Байкальского региона