Magnetic and structural properties of all-D metal Mn-Ni-Ti Heusler alloys

In recent years, Ni-Mn ferromagnetic shape memory alloys have been extensively researched for commercial applications owing to their diverse multifunctional characteristics, including the magnetic shape memory effect, magnetocaloric effect, and magnetoresistance arising from temperature- or magnetic field-induced martensitic transformations [1–6]. However, challenges related to poor mechanical durability and significant hysteresis losses during phase transitions limit their practical application.

Recently, Heusler alloys have been developed that contain all d -transition metal elements based on nickel (Ni), manganese (Mn), and titanium (Ti) [7–9]. In these alloys, Ti replaces the elements from the p -block, and it has been shown that the d -block Ti metal provides stabilization of the Heusler structure through d - d hybridization with its nearest neighbor element [10]. These alloys exhibit an ordered L2 1 structure and an partially disordered B2 structure, and they undergo a phase transition from B2 to L2₁, which is accompanied by a change in structural order and a martensitic transformation at a lower temperature. In the B2 phase, some Mn atoms exchange positions with Ti atoms, leading to a strong antiferromagnetic interaction between Mn atoms located at different crystallographic sites.

A distinguishing feature of all- d metal Heusler alloys is their large relative volume change during the martensitic transformation process, which is significantly greater than in any other ferromagnetic shape memory alloy. This characteristic indicates a notable sensitivity of the transformation to applied mechanical stresses, particularly hydrostatic pressure. This makes these materials well-suited for demonstrating significant barocaloric effects. For example, Wei et al. [11] showed that a compressive stress of 900 MPa results in a deformation of approximately 3,9 % and an adiabatic temperature change of 10,7 K in Ni₅₀Mn₃₂Ti₁₈ alloy. Yan et al. [12] observed large deformations of approximately 13 % in the Ni₅₀Mn_31,75Ti_18,25 alloy under a compressive stress of 1,1 GPa. Due to the weaker d - d orbital hybridization in transition metal elements, there is a notable enhancement in mechanical properties, particularly improved plasticity, compared to conventional Heusler alloys that contain main group elements in combination with a strong p - d orbital interaction.

In this paper, we paid attention to the theoretical study of the effect of atomic ordering on the structural and magnetic characteristics of Mn 2 Ni 1+ x Ti 1– x alloys within the framework of density functional theory.

• 1.    Details of calculations

• 2.    Results and discussions

The calculations presented in this paper were performed within the framework of density functional theory, using the projection-augmented wave (PAW) method, which is implemented in the VASP software package [13, 14]. A series of Mn 2 Ni 1+ x Ti 1- x Heusler alloys, consisting entirely of transition metals, were selected as the objects of study. The exchange-correlation energy approximation was realized using the generalized gradient approximation for electron density in the Perdew–Burke–Ernzerhof parametrization [15]. The following valence electron configurations were considered in the PAW potentials: 3 s ²3 p ⁶4 s ²3 d ⁵ for Mn, 3 p ⁶3 d ⁸4 s ² for Ni, and 3 s ²3 p ⁶4 s ²3 d ² for Ti. The plane wave basis cutoff energy was set at 450 eV, and a Monkhorst-Pack grid with a size of 8×8×8 was used for integration over the Brillouin zone. Geometric optimization of the 16 atom cells with cubic (L2 1 , Fm 3 m , No. 225, and XA, F- 43 m , No. 216) and tetragonal (T^p, P 4/ nmm , No. 129) symmetries was performed using atomic position relaxation at constant volume and cell shape, with convergence criteria for energy and force equal to 10^-6 eV and 10^-2 eV/Å, respectively. Nonstoichiometric compounds were created by sequentially replacing Ti atoms with Ni. The following magnetic configurations were considered for the spin ordering of Mn atoms (see fig. 1): FM (ferromagnetic state), AFM (antiferromagnetic state with staggered arrangement of magnetic moments), and AFM* (antiferromagnetic layer-like arrangement of magnetic moments).

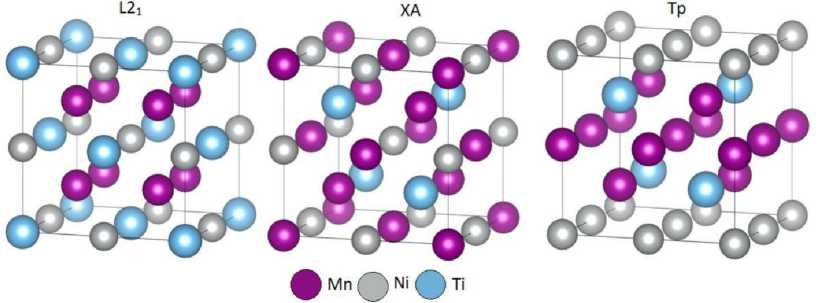
Fig. 1. The crystal structures of Mn 2 NiTi Heusler alloy with cubic (L2 1 , Fm 3 m , #225, and XA, F- 43 m , #216) and tetragonal (T^p, P 4/ nmm , #129) symmetry. The L2 1 and XA structures differ due to the placement of Mn atoms in equivalent and non-equivalent positions, respectively. The T^p structure is based on the XA structure and composed of layers of Mn and Ni atoms alternating along the [001] direction [16, 17]

The magnetocrystalline anisotropy energy (MAE) was calculated by performing successive self-consistent calculations that took into account spin-orbit interaction for structures with magnetic moment orientations along [001] and [100]. The MAE was then determined using the wave functions obtained from the self-consistent calculations. To obtain the MAE, the difference between energies E ₁₀₀ and E ₀₀₁ was evaluated. Here E ₁₀₀ and E ₀₀₁ are the total energies of the compounds with the corresponding magnetic moment orientations. A negative MAE value indicates easy plane anisotropy, while a positive value corresponds to easy axis anisotropy.

This section discusses the results obtained for a set of Mn₂Ni_{1+ x} Ti_{1- x} alloys ( x = 0, 0,25, 0,5 and 0,75). The procedure of geometrical optimization of Heusler crystal structures of L2₁, XA and T^p types was performed, taking into account their different magnetic ordering, to establish the energetically preferable structure for each compound. We would like to note that the T^p structure has been originally proposed by Neibecker et al. [16].

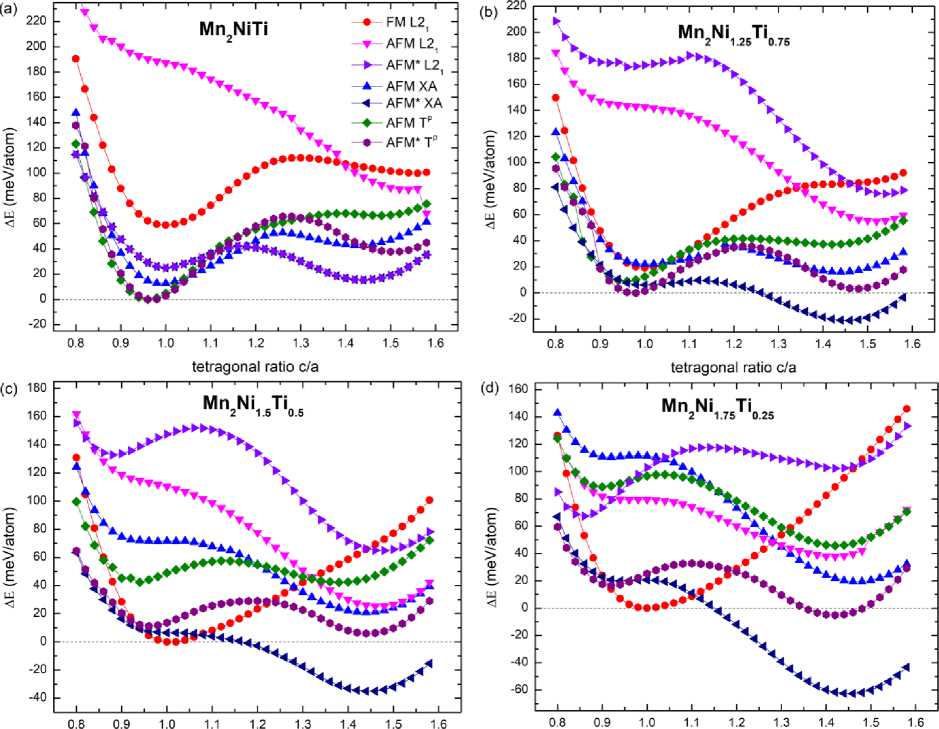
Fig. 2 clearly demonstrates the variations in total energy of the cubic structures based on their degree of tetragonal distortion c / a . It should be noted that the presence of a stable martensitic tetragonal phase in the alloy is indicated by a global energy minimum on the curve E ( c / a ) at c / a ≠ 1.

As can be seen from Fig. 2, a , for the stoichiometric compound Mn 2 NiTi, layered atomic ordering of Ni and Mn is energetically favorable, thereby pointing to the T^p structure as the ground state of the austenite phase ( c / a ≈ 1), despite the fact that each of the structures exhibits pseudo-martensitic behavior at c / a > 1. The magnetic reference state of T^p structure is characterized by AFM* (layer-by-layer) ordering of the Mn spin moments. The energy difference between the T^p and XA, L2₁ structures with AFM* ordering is about 12,8 and 24,9 meV/atom, respectively. The FM solution for Mn₂NiTi is located signifi-

Физика cantly higher on the energy scale, indicating its disadvantage. It should be noted that the XA and L21 structures have been experimentally observed in Heusler alloys, whereas the theoretical Tp structure has not been yet experimentally confirmed. Several theoretical papers [17-19] have reported the energetic favorability of the Tp structure for Fe- and Co-based Heusler alloys.

tetragonal ratio c/a                                                      tetragonal ratio c/a

Fig. 2. Variation of the total energy of the cubic crystal structures L2 1 , XA and T^p taking into account FM and AFM ordering as a function of the degree of their tetragonal distortion for Mn 2 Ni 1+ x Ti 1- x alloys

Partial substitution of Ti atoms with excess Ni atoms results in a stable tetragonal phase with atomic ordering of the XA structure type (see Figs. 2, b – d ). The layered antiferromagnetic ordering of Mn magnetic moments is energetically favorable in the martensitic phase for all non-stoichiometric compounds. In this case, the Mn atoms are located in two non-equivalent sublattices and are at the closest distance to the other atoms. It should be noted that an increase in the Ni content leads to a change in the ground state of the austenitic phase ( c / a = 1). Thus, Fig. 2, b demonstrates that the T^p structure remains stable for the compound with x = 0,25, despite the smaller energy difference, ∆ E ≈ 6,42 meV/atom, between the AFM* T^p and AFM* XA structures compared to the value of ∆ E ≈ 12,8 meV/atom for Mn 2 NiTi. Further increase in Ni content ( x > 0,25) results in the instability of T^p structure for austenite phase. Similar finding has been reported recently for FeNi_{2+ x} Al_{1– x} alloys [17]. It is obvious from Fig. 2, c , d that an increase in x changes the atomic and magnetic ordering of the cubic austenite phase from AFM* T^p to FM L2 1 one. For the L2 1 structure, Mn atoms occupy equivalent positions at a greater distance ( d = 0,5 a 0 ) compared to the case of the T^p structure ( d = √3/4 a ₀). An increase in the distance between Mn atoms causes a change in the nature of the magnetic interaction from AFM to FM.

The E ( c / a ) curves for the Mn 2 Ni 1+ x Ti 1– x compositions indicate that the martensitic transition temperature T_m will increase with increasing Ni content. This is a result of the heightened energy barrier between the cubic and tetragonal phases. Replacing Ti atoms with Ni atoms increases the concentration of valence electrons ( e / a ) per atom, resulting in a corresponding increase in the energy barrier with concentration x . This observation is consistent with the experimentally established linear dependence T_m ( e / a )

Table 1 summarizes the equilibrium lattice parameters, total and elemental magnetic moments for the energetically favorable crystal structures of the compounds Mn₂Ni_{1+ x} Ti_{1– x} , taking into account a magnetic reference ordering. The table clearly demonstrates that the equilibrium parameter of crystal structures in the austenitic phase increases as the Ni content increases. This is due to the larger atomic radius of Ni atoms compared to Ti atoms. However, the tetragonal structure parameters of the martensitic phase with XA ordering exhibit an ambiguous behavior that is dependent on the Ni content.

Table 1

Equilibrium lattice parameters ( a and c ), tetragonal ratio ( c / a ), total and elemental magnetic moments (µ tot and µ i ) in [µ B /f.u.] and [µ B /at.], respectively, for Mn 2 Ni 1+ x Ti 1- x alloys in cubic austenite and tetragonal martensitic phases. All parameters are presented for energetically favorable structures and magnetic configurations: AFM* T^p ( x = 0 and 0,25), FM L2 1 ( x = 0,5 and 0,75) for austenite; AFM* XA ( x = 0,25, 0,5 and 0,75) for martensite

Compound	Parameters	x = 0	x = 0,25	x = 0,50	x = 0,75
	a	5,805	5,82	5,88	5,86
	µ tot	3,275	2,657	6,87	7,817
austenite	µ Mn1	–0,282	–0,842	3,10	3,323
( c / a =1)	µ Mn2	2,975	2,992	3,10	3,323
	µ Ni	0,475	0,434	0,796	0,821
	a		5,130	5,136	5,113
	c		7,490	7,396	7,464
martensite	c / a		1,46	1,44	1,46
( c / a ≠ 1 )	µ tot		0,425	0,238	0,176
	µ Mn1		2,509	2,688	2,981
	µ Mn2		–2,217	–2,534	–2,865
	µ Ni		0,027	0,032	0,009

The behavior of magnetic moments shows a clear trend: the total magnetization decreases for compositions with T^p structure and AFM* ordering of Mn₁ and Mn₂ atoms. This is a result of the increased magnetic moment of Mn 1 atoms located in the (002) plane, while Mn 2 atoms occupy tetrahedral positions in the T^p structure (see Fig. 1). Compounds with L2₁ ordering in the austenitic phase ( x = 0,5 and 0,75) exhibit an increase in total magnetization. This is attributed to the growth of the element-by-element magnetic moments of Ni, Mn 1 , and Mn 2 atoms. It is worth noting that the difference between Mn₁ and Mn₂ is purely conventional, as these atoms occupy equivalent positions in two interpenetrating FCC sublattices (refer to Fig. 1). The data clearly shows that as the Ni content increases, the total magnetization of the martensitic phase with XA ordering decreases significantly. This is due to the antiferromagnetic orientation of the magnetic moments of Mn₁ and Mn₂, which are located in non-equivalent positions (0, 0, 0) and (0,25, 0,25, 0,25) respectively (see Fig. 1). It is also worth noting that the magnetic moment of Ni atoms is suppressed. The binary compound Ni-Mn, resulting from the substitution of Ti for Ni, exhibits antiferromagnetism with a Neel temperature of around 1000 K [3, 20].

To calculate MAE, we chose the magnetic states of tetragonally distorted structures XA, L1₀, and T^p of Mn 2 Ni 1+ x Ti 1– x compounds, as presented in Fig. 2, due to their close energy levels. Our selection of these structures was based on their energy levels and their suitability for accurate calculations. For the x = 0, we have considered the AFM* T^p ( c / a = 0,96), and AFM* L1₀ ( c / a = 1,44) structures. For the x = 0,25, we have taken the AFM* XA ( c / a = 1,46), and AFM* T^p ( c / a = 0,98) structures. Finally, for the x = 0,5 and x = 0,75, we have considered the AFM* XA ( c / a = 1,44 and 1,46), and AFM* T^p ( c / a = 1,44 and 1,42) structures, correspondingly.

Fig. 3 shows the histograms of MAE calculated for crystal structures mentioned above. Here, the negative sign of MAE indicates the energetically favorable in-plane spin direction and easy plane MAE, and vice versa the out-of-plane spin direction and easy axis MAE. For all compounds with tetragonally distorted AFM* XA and T^p structures, the easy-axis-type anisotropy is observed except Mn 2 NiTi with tetragonal L1₀ structure, where the easy-plane-type anisotropy is preferable. In a case of compounds with x = 0 and 0,25, T^p structure with nearly cubic parameters ( c / a = 0,96 and 0,98) demonstrates a considerable MAE, which is comparable with that of compounds with tetragonal structures ( x = 0,5 and

Физика

0,75). The largest MAE value is calculated to be 0,4 MJ/m³ for AFM* XA structure ( c / a = 1,46) of Mn₂Ni_1,25Ti_0,75. However, for compounds with x = 0,5 and 0,75, the T^p structure reveals a larger values of MAE as compared to the XA structure. We would like to mentioned that the calculated values of MAE are comparable to those of L1₀-FeNi (0,22 – 0,48 MJ/m³ [21–24]), which is the most intensely discussed candidate for high-performance rare-earth-free permanent magnets.

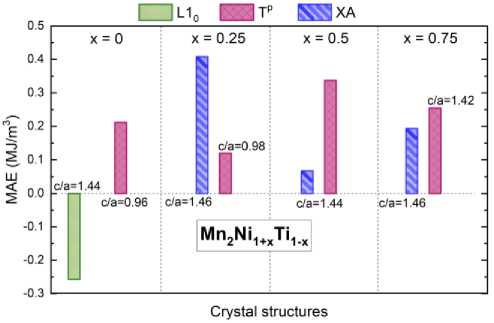
Fig. 3. Magnetocrystalline anisotropy energy diagram for tetragonally distorted L1 0 , XA, and T^p structures of Mn 2 Ni 1+ x Ti 1- x alloys ( x = 0, 0,25, 0,5, and 0,75) with the favorable magnetic configurations

Conclusions

In summary, we have performed the ab initio investigations of the influence of atomic and magnetic ordering on the ground state energy and magnitude of magnetocrystalline anisotropy for Heusler alloys of the Mn-Ni-Ti family, which consist entirely of transition d metals. For stoichiometric compound Mn₂NiTi, an energetically favorable structure T^p with nearly cubic lattice parameters and layer-by-layer ordering of Mn and Ni atoms is predicted. This structure is characterized by the antiferromagnetic spin alignment of Mn magnetic moments. Furthermore, this structure demonstrates an easy-axis magnetocrystalline anisotropy of about 0,2 MJ/m³, which is not typical of cubic phases. When Ti atoms are partially substituted with Ni, stable tetragonal structures T^p and XA emerge, which are ordered antiferromagnetically. An increase in Ni content results in a higher energy barrier between cubic and tetragonal phases, indicating a rise in the martensitic transition temperature. It was found that the Mn₂Ni_1,25Ti_0,75 compound in the tetragonal XA structure with c / a ratio of 1,46 exhibits the highest MAE value of 0,4 MJ/m³. Nevertheless, for compounds with x = 0,5 and 0,75, the tetragonal T^p structure also exhibits larger MAE values compared to the XA structure. Overall, the MAE values obtained are comparable to those of tetratenite L1₀-FeNi, which is an alternative to rare-earth-free permanent magnets.

This study was supported by the Russian Science Foundation (RSF), Project No. 24-12-20016.