Магнитное поле звезд, находящихся в динамическом равновесии

В работах [1, 2] была предложена модель автомодельной динамики звезд и других астрофизических объектов, основанная на идее динамического равновесия таких объектов. В отличие от статического равновесия динамическое равновесие учитывает наличие автомодельной эволюции астрофизических объектов, обусловленных неточным балансом между силой тяготения и силой Архимеда, приложенных к элементарному объему газа. Характерной особенностью такого равновесия является наличие радиального потока Хаббла и специального зонального потока, увеличение или уменьшение которых со временем и в пространстве дает вклад в баланс сил.

Методология динамического равновесия опирается на математический аппарат теории гидродинамических маркеров [3-6], что позволяет получить общие соотношения для плотности среды и напряженности гравитационного поля в терминах гидродинамических маркеров. В работе [2] этот подход использовался для построения модели пульсаций звезд, которая была применена для описания почти радиальных пульсаций Солнца и других звезд, в том числе, цефеид. В рамках этой модели удалось объяснить 11-летний цикл солнечной активности.

В модели динамического равновесия в звездах существуют гидродинамические потоки плазмы. Наличие таких потоков обязательно должно порождать магнитное поле. Например, изменения солнечной активности прослеживаются на основе наблюдения пятен на Солнце. Пятна же на Солнце тесно связаны с магнитными аномалиями в его фотосфере. Поэтому логичным развитием идеи динамического равновесия и автомодельных осцилляций звезд является задача включения в общую модель и динамики их магнитного поля. Следует отметить, что в статических моделях звезд отсутствуют потоки плазмы, которые являются основными генераторами магнитного поля. В рамках моделей динамического равновесия магнитное поле генерируется течением плазмы, связанным с автомодельными изменениями структуры звезд. В результате появляется возможность включить в модель осцилляций звезд и их магнитное поле. Решению этой задачи и посвящена данная работа.

В начале данной работы в кратком виде излагаются основные элементы модели динамического равновесия звезд [2] и приводятся основные результаты, относящиеся к модели Солнца. Затем вычисляется магнитное поле звезд в предположении слабого магнитного поля, которое не оказывает заметного влияния на гидродинамические потоки в звезде. В конце работы строится самосогласованная модель звезды с магнитным полем и анализируются модифицированные уравнения автомодельной ее эволюции.

1.    Общие уравнения замагниченной плазмы в собственном поле тяготения

Уравнения идеальной замагниченной плазмы в собственном поле тяготения можно записать в следующем виде [7-9]:

> =- ；"^ +)卜 0tH X Н] , Ж +div ( p v ) =0, △ 0 = 4?rGp, д Н - = rot [v X н] , div H = 0, Р = P ( P,s) ・

(LI) (1-2) (1.3) (1.4) (1.5)

Далее в работе данная система будет рассматриваться в цилиндрической системе координат г, г, g вместе с условием цилиндрической симметрии, т.е. отсутствием зависимости функций от азимутального угла g. В этих уравнениях p ( r,z, 。— давление газа, u ( r,z, 。， з ( г,г, 。， v ( r,z, 。— компоненты скорости гидродинамического потока, p(r, г, 。一 плотноеть массы, 0(г, г, 。一 потенциал поля тяготения, G — постоянная тяготения Ньютона, г и г — радиальная и вертикальная координаты, 力— время. Вектор H = Н ( г,г, 。— напряженность магнитного поля. Уравнение (1.5) является уравнением состояния газа, где б(г,г, 。一 локальная энтропия газа. Наличие компоненты скорости з(г,г, 。 потока в зональном направлении эквивалентно дифференциальному вращению структуры вокруг вертикальной оси г.

В начале будем предполагать, что обратное влияние магнитного поля на гидродинамические потоки плазмы в звездах типа Солнца мало и им можно пренебречь в нулевом порядке теории возмущений. Это означает, что в уравнении (1.1) последним слагаемым в правой части можно пренебречь. В этом случае все выкладки, которые приведены в [2] остаются в силе, а магнитное поле описывается векторным уравнением (1.4). Это единственное уравнение, которое необходимо добавить к модели в случае слабого поля, рассмотренной в [2] в случае малого магнитного поля.

2.    Модель динамического равновесия звезд

В цилиндрической системе координат уравнения динамики самогравитирующего газа (плазмы) (1.1)-(1.3) с учетом сделанных замечаний можно записать в такой форме:

U t + ии_г + wu_z

。 ²

г

- рР г - ф г ,

Wt + U^r + WWz = - pPz - Oz,

伙 + U^r + W^z + —- = 0, r

(2.1)

P 方 +

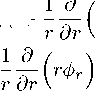
丁 и 。 ) + / ( Р^) = ° ， ^d

+ kOz = 47rGp.

oz

(2-2)

(2.3)

Эта система описывает динамику звезды без магнитного поля, которая и исследовалась в [2].

В качестве уравнения состояния при описании динамического равновесия в [2] используется предположение, что газ (плазма) имеет состояние, близкое к идеальному газу:

р = — рТ.

Мд

(2.4)

Здесь / — универсальная газовая постоянная, ^ д — молярная масса га ： за. Т — абсолтотиая температура. Полагая, что процесс переноса плазмы в звездах является глобально адиабатическим, т.е. энтропия не меняется вдоль линий тока, приходим (см. Приложение 1 и [2]) к следующему общему уравнению состояния:

р = Kes/ 。 。 pi,

(2.5)

где 6 — энтропия. c_v — молярная теплоемкость при постоянном объеме ii 7 — пока ，： за ， те, 「 ь адиабаты. Параметр K связан с состоянием газа ， при какой-то выделешюп температуре.

2.1. Динамика маркеров, плотность вещества и уравнение состояния

Основой теории динамического равновесия является введение в теорию гидродинамических маркеров e ^a (r, z, t), q = 1, 2. с помошьто которых описыватотся все основные динамические параметры структуры звезд. Уравнения переноса маркеров можно записать в следующие виде:

瓦+工+f

0, q = 1, 2.

⑵ 6)

Здесь и далее будем использовать правило суммирования по повторяющемуся индексу. Система допускает дифференциальное тождество, которое можно записать в следующем виде (см. в [1,2]):

"+ / ( ^UIJ I ) ⁺ JZ (®J 卜 ⁰,                      ( 27 )

где (функция IJI — якобиан преобразоватшя от координат z, r в координаты e1,e2 пространства значений маркеров:

|JI = I det J |.                                                        (2.8)

Здесь

人

J

еГ   ez еГ   ez

⑵ 9)

Отсюда следует, что любая функция:

р = M o |J |/г,

(2.10)

удовлетворяет уравнению неразрывности и может интерпретироваться как плотность среды. Здесь Mo — масштабный коэ ( 1 )( 1 ) шпіепт. иметоттпіп размертюс 工 ъ массы. В этом случае (2.7) эквивалентно уравнению неразрывности (2.2).

2.2.    Уравнение Пуассона и маркеры

Рассмотрим теперь формальное тождество:

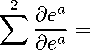
де1   де2

——+ —— де1 де2

а =1

(2.11)

Переходя в этом тождестве к физическим координатам т1 = г, т2 = г, получаем следующую форму этого тождества:

2|j |.

(2.12)

Это тождество можно превратить формально в уравнение Пуассона для напряженности гравитационного поля g. Представим это уравнение в таком виде:

д ( |J 1 小) +     ( |j|к2 ) =2|j|,                              ( 2.13)

где

K 1 =

22 工 еЬ£, K2 = Е е ， Ц.                   (2 」 4)

Учитывая то, что производные дх ^а /де^а являются элементами матрицы, обратной матрице Якоби J (2.9[ находим:

и | л = i^' ^{i j} | л =-*

|J|ІІ = -ІР ^{| j} |Ž2 = *

Отсюда:

।丿 1 小=£ е 1 - ^е², |^j| K 2 = Це² - 臨 е¹.                (2.15)

Соотношение (2.13) с учетом (2.10) можно переписать теперь так:

1 д ( 2ttGM o | J I г дг       г

1 ) + 兴 2 〃 GM ° 叨 K 2 ) = 4f2MM =4M,     (2.16) / дг \         г /         г

Сравнивая уравнение Пуассона (2.3) с уравнением (2.16), находим:

-0, 7 9 1 == -2^ 0 |j|К 1 - 1 厶 ,

-0Z 7 9 2 = -2^^ ° |jIK² + 1 田 ,,                      (2.17)

где 9а, а = 1,2 — компоненты вектора ускорения свободного падения, a W(r, г, 。— некоторая произвольная дифференцируемая функция. Компоненты ускорения свободного падения g для любой дифференцируемой функции W(r, г, 。 в силу (2.17) удовлетворяют уравнению:

1 д ,      、 ， д ,

而 ⁽ 『 ^{91 )} + 石( ⁹² )= ⁴"Gp.

Это и позволяет интерпретировать g как компоненты ускорения свободного падения.

Вместе с тем при интерпретации g (2.17) как вектора напряженности поля тяготения возникает определенная сложность, состоящая в том, что g с компонентами (2.17) не обязательно будет градиентом некоторого потенциала ф. В работах [1,2] вместо (2.17) использовались соотношения:

91 = -ф , = - ^27r °皿 \J |К¹ +Ф 乞 ， г

92 = -ф 乞 =- 27 ： М0 \ J\к2 + ф , ,                         (2.18)

в которых гарантируется условие потенциальности g. При этом функция Ф должна удовлетворять уравнению:

¹ (гФ , ) +   Ф_г = 0.

г dr         oz

В случае выбора (2.18) при условии, что слагаемое с давлением оказывается градиентом некоторой функции, g также оказывается градиентом некоторого потенциала. В случае же (2.17) такой гарантии нет. Это означает, что в таком подходе поле тяготения при определенных условиях будет содержать некоторую вихревую добавку, которую можно назвать гравимагнитным полем [5,6,10]. В данной работе будет рассматриваться общий вариант (2.17), который дает возможность построить более близкую к данным модель Солнца, в которой зональный поток имеет зависимость от вертикальной координаты z, чего невозможно добиться в рамках моделей с (2.18). Этот вопрос будет обсуждаться далее более подробно.

2.3.    Зональная и радиальные составляющие потока

С учетом (2.17) уравнения для радиальных составляющих потока u и w можно записать в таком виде:

坎 + uu, + wuz — — = - -p, - 27GM0 \ J\к1 -丄屮乞, r р        r            r wt + uw, + wwz = - -pz — 27rGM0 । j\k2 + 丄屮，,                   ( 2.19 )

р        r            r где W(r,z," — произвольная дт])(])еренп,ііруем>і，я (функция.

Гидродинамический поток в моделях статического равновесия звезд отсутствует. В теории динамического равновесия поток существует и состоит из радиального потока с компонентами:

u = Н ⑴ r, w = F ⑴ z,                            (2.20)

и зонального со скоростью 。 = ^(r, z, t). В случае выбора радиального потока в форме (2.20), что аналогично закону Хаббла в космологии, маркерные функции е^а = e^a(r, z, t) являются произвольными функциями двух автомодельных переменных:

€ = r/a(t), С = z/6(t).                                      (2.21)

Фуііктпш q = @(t) ii b = b(t) па：зыватс)тся масштабными (факторами, а(])ункп,ші： qb

Н = —, F =7                                  (2.22)

qb

• —параметрами Хаббла. Далее будем использовать следующие обозначения:

е 。 = £^а(€,С), q =1,2.

Плотность среды в автомодельные переменных будет иметь такой вид:

р = Q(t)2b(t) Аде, где:

R— - -Cl / — det 程经 反 -g , J _det 用受

(2.24)

Фуііктіпто 冗 (g, С) в дальнейшем будем иггзывать коэ<1 ) <1 ) шпісптом плотности. Из этого следует ：

| J |小=	=1 （ 戶 1 经_产变 方     дС     d	J = ； 〈 (go,
| J | K2 =	- ：( £1 dg2 *	貫) =: 〈 2(g,c

(2.25)

Функции 〈 1 и 心 удовлетворяют в силу (2.13) уравнению:

gdg ^(g 〈 i ) + de 〈 2 =^2|J|-

(2.26)

В терминах маркерных полей e^a(r, z, 。 выражается и зональная компонента скорости потока.

Третье уравнение системы (2.1) в такой форме:

(А ++° _。 ，

\ ot dr dz 丿 где £ = u(r, z, t)r — удельная плотность момента импульса среды. Отсюда следует, что функция £(r, z,t) является фуикцией маркеров £ = £(е1, е2) и следовательно :

。 二 ^{£ ( е 1} ， ^{е 2 )}

.

г

Это соотношение позволяет замкнуть описание динамики газа в терминах маркерных полей.

Уравнение состояния (2.5) теперь можно записать в следующем виде:

(2.27)

р = a(t)S(g, С ) p^ =。⑴ a-S ( t ) S ( g,C ) M^ 冗 ' ( g, С ) .                    (2.28)

Здесь o ( t ) = eS0 ( * ) /cu и S ( g, С ) = £勾 ⁽ £<)/加 —коэффициент энтропии. Вычисление множителя o ( t ) приведено в [2]. Соответствующее соотношение для температуры будет иметь такой вид:

Т = Kca(t)S(g, С)р' ^{- 1} = n(t) 丁 (g, С),

(2.29)

(2.30)

где

n(t) = Ko°(t) 叫 TQ ^{- 2} ( 'T ) b ^- '⁺¹, 7(g, С) = S (g,C) 冗 'T(g,C) ・

Функтціто 7 = 7(g, С) будем па ： зывать коэ ( 1 )( 1 ) шпіептом температуры.

• 3.    Уравнения в автомодельных переменных

  3.1.    Общий вид уравнений в автомодельных переменных

Уравнения для u и w в автомодельных переменных с учетом (2.20), (2.28), (2.17), (2.23) и (2.27) принимают такой вид:

a(" + "2 ) g — 个 = —      (SA) — 吋〈 1 — , Q3g3        Q 冗 dg            Qb        Qb g 6(Ғ + Ғ2)С = -予!垃 (SR) - ” 〈 2 +』学 .             (3.1 ) b 冗 дС \     丿       Q2         Q2 g

Для возможности разделить переменные в этих уравнения выберем вид функций £(g, С) и W(g, С, t) следующим образом:

£ ² = /i g⁴ + 〃 (С )g², 田 =/2 9 Сg² + 卜 (С)+2 亓 GMo%(g,Q.            (3-2)

Здесь /1, /2, а — некоторые постоянные, а п(С) — некоторая произвольная дифференцируемая функция переменной 《. Подставляя соотношения (3.2) в уравнения (3.1), приходим к такой системе уравнений:

m+ " :2 ) -少卜:卜发四)「] 1 ① +%<[ …:²T 卜一叭为(叱) - 吋 1 &一泣     (3.3)

Неизвестными в этих уравнениях являются масштабные факторы q( 。， b(t) и маркеры £ 1(£<) , £ ²(£<)■ ^'равнения (3.3) теперь допускают ра ， зде, 「 етше переменных.

Выбор W в виде (3.2) приводит к тому, что напряженность поля тяготения g может перестать быть потенциальным полем. Действительно, для того, чтобы поле g в конечном итоге было потенциальным, должны выполняться два соотношения. Первое состоит в требовании, чтобы коэффициент энтропии был функцией коэффициента плотности: S( £,《 )=S( 冗 ).Второе требование согласно (2.17) можно записать так:

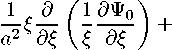
1 д 2%

Ь2 "2

(3.4)

4.    Разделение переменных

Условиями разделения переменных являются следующие соотношения:

b = /3@ (。， В = const,

П = Q 9,

(4.1)

(4.2)

(4.3)

Q

。 ( 方 + Н 2 ) - % =л" , Q³          ра²

/ 1 + / 2 = -2/ 2 .

В этом случае уравнения пространственного распределения £ 1, £2 имеют такой вид:

^л£² = —Q^ 振 (sa ) — R^{1 -} %с ^ЛС£ = -Qp ^ 天 (sa ) ^- 〈 ² + %<•   (4 ・ 4)

Для анализа пространственного распределения плотности и температуры нет необходимости явно вычислять функции £¹ и £². Из последних двух уравнений можно сконструировать одно уравнение отпосителыю 冗 либо Т. Для этого первое уравнение не обходимо продіі ( 1 )( 1 ) ерептпіровать по & а второе по С ii ре ： зультаты сложить ：

3Ag + Q

(d [然 Gr )]+浦

р² 冗 дС

( sr )]) + r = 0.

(4.5)

Поделив последнее уравнение na g, приходим к обобщенной автомодельной версии уравнения теории Лейна-Эмдена:

А + ^Qg [ (SR )1 + 冬 [ 恥 g (SR')1 + R = 0.            (4.6)

g dg |_R dg \     / J dC |_P²R dC \ 丿

Здесь введено обозначение: А = 3Л/2 и без ограничения общности полагается 2Q = 1. Последнее уравнение содержит в качестве неизвестной функции только функцию R.

5.    Уравнения эволюции

В результате разделения переменных эволюция структуры со временем описывается уравнением для масштабного фактора а ⑴， а пространственное распределение температуры и плотности уравнением (4.6).

Уравнение эволюции (4.2) можно представить в следующем виде:

〃_" Q Q³    Q² .

(5.1)

Здесь введены обозначения:

〃 =2^GM o A, 〃 = / 1 + 力 =3/ і /2.

(5.2)

Уравнение (5.1) удобно привести к виду безразмерной динамической системы. Для этого введем переменные:

т = q/q o , у = т , 丁 = 力/力 о ,

(5.3)

где:

^Qo = 〃/冋^， h

〃 3 / 2

.

(5.4)

В результате система принимает такой вид:

1 s у = т3 + T2，

т = у.

(5.5)

Здесь 6 = sign” = sign А. Эта модель имеет интеграл энергии:

у²* 1 亠 ¹

万+ ⁶T +五 2

2T2

е,

(5-6)

Фазовые портреты системы для s = 1 и s

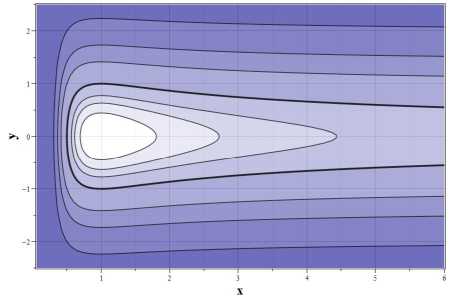
а

Рис. 1. ① азовыіі портрет (5.5) а) для 〃 <  0: Е = -0 . 5 (0), Е = -0 . 4(1), Е = -0 . 3(2), Е = -0 . 2(3), Е = 0.0(4). Е = 0.5(5) Е = 1.0(6). Е = 2.0(7) ： Ь) для 〃 > 0: Е = 0.125(1). Е = 0.25(2) Е = 0.5(3). Е = 1.0 (4). Е = 2.0 (5). Е = 4.0 (6)

— 1 Приведены на рис. 1 (а.1. ) )_

b

6.    Пространственное распределение температуры

Уравнение (4.6) содержит кроме неизвестной функции 冗 ( £,《 )фуикцию S( £,《)— коэффициент энтропии, который необходимо вычислять из каких-то других соображений. В работе [2] для этого предлагается использовать общее соотношение следующего вида:

S =亚()紹 .

(6.1)

Функция "(£<) должна, описывать отклоііеіше распределения энтропии от политропного распределения. Строго политропное распределение энтропии, т.е. зависимость S толь ко от 兄 является следствием общего представления, что коэффициент непрозрачности вещества звезды и энерговыделение в них являются степенными функциями температуры и плотности среды. В работе [2]

предполагалось, что 我 =1. Показатель 8 в (6.1) подбирался с помощью сопоставления результатов численного счета с реальными данными для Солнца. В случае 我 =1, как можно проверить, уравнение (4.6) не меняет своей формы, но в нем показатель адиабаты самого газа 7 заменяется на новый эффективный показатель 7' по формуле 7' = 7 + 8. При этом уравнение выглядит следующим образом:

X+/d!       (r‘)] +         :(a‘)] + 穴 = ^{0 .}

(6.2)

Для описания почти сферических звезд перейдем в уравнении (6.2) от цилиндрических координат к сферическим. Соответственно уравнение (6.2) примет следующий вид:

一《卜 ^{2 (}一 S" + s 初 + 击/ 卜 " (一 5 丁 + s 砌+ 厂 + 人 =⁰-⁽⁶-³⁾

Здесь X = ，£ ² + 〃 ²i! 9 = arctg( £/〃)— радиальная координата и полярный угол соответственно. По аналогии с моделями Лейна - Эмдена в качестве граничных условий для безразмерной функции ^ ( X, 9), записанной в сферических координатах, будем рассматривать два условия:

冗 (0,9) = 1, ?冗 (х,9)    =0.

(6.4)

°х       х =0

Первое из этих условий фактически связывает масштаб плотности газа в исследуемых объектах, например, неопределенный пока параметр М°, с его плотностью в центре поля. Второе условие необходимо для того, чтобы исключить сингулярные в центре поля решения. Отсюда также следует граничное условие для S(х, 9):

氏 %'⁹ )

=0, (6.5)

Х =0

которое также необходимо для исключения сингулярных в точке х = 0 решений в случае неоднородного распределения энтропии. Граничным условием по угловой координате, как обычно, следует считать условие периодичности.

7.    Наилучшая модель Солнца

В работе [2] приведена методика определения параметров модели, исходя из набора основных параметров звезды. В качестве таких параметров взяты следующие параметры: радиус звезды 凡， плотность в центре звезды р* = р(0), температура в центре звезды 厶， скорость зонального потока на экваторе звезды ^* и показатель политропы 7. Для Солнца эти параметры приведены в Таб. 1.

Таблица 1. Основные параметры Солнца

Параметр	Значение
Радиус R q	7 • 108[см]
Экваториальная скорость 。 @	2 • 105[см/с]
Показатель адиабаты 7	5/3 (Одноатомный газ)
Плотность в центре p q	150 [г/см3]
Температура в центре TQ	-15 • 106 [К]

Как показано в работе [2] наилучшей моделью для Солнца является модель со следующими значениями параметров модели, которые были получены с помощью численных расчетов:

Распределение коэффициентов температуры 「 плотности 冗 и энтропии S, соответствующие наилучшей модели, представлены на рис. 2 (а,Ь).

Таблица 2. Параметры наилучшей модели для Солнца

Параметр	Значение
Показатель энтропии 8	--7/15
Эффективный показатель адиабаты 7‘ (с учетом потока тепла)	-6/5
Р (Е*)	—11.03 [год]
А*	--7.788 • 10-12
Хо	-13537
Xi	-132000
Tmin	-6•10-3
7 ^〃 п = 7т 〃 п7^	-4500 [К ]
^таж	-0.00717
Т тан = Ттаж^О	-101000 [К]
£	-6•10-5

8.    Уравнения для магнитного поля

В случае динамического равновесия звезды со слабым магнитным полем, т.е. таким полем, которое не оказывает заметного влияния на структуру гидродинамического потока плазмы, уравнениями для напряженности магнитного поля являются уравнения (1.4), в котором компоненты гидродинамического потока определяются соотношениями (2.20) и (2.27) с учетом (2.13). Для анализа уравнений динамики магнитного поля введем следующие обозначения:

H = (hr,hz,%), где hr — радиальная составляющая магнитного поля, h^ — вертикалыіая, a h^ — зональная. Первое уравнение для H полезно (раскрывая двойное векторное произведение) записать в следующем

виде:	d H +( v ，▽ * ：	=( H , V) v — H div v .		(8.1)
В покомпонентной записи уравнения (1.4) можно записать в такой форме:
dh r dt	dhr    dhr + U-^..+ V-^-: dr     dz	=—Hhr,
dhz dt	,dhz ,    dhz + "二.. + 仅方一 dr     dz	=—Hhz,		(8.2)
dh 屮 dt	+ 年 +m* dr     dz	+ 2Hhg =	( hr / + hz dZ 卜
dh r dr	dhz + 宗 =0. dz			(8.3)

Для упрощения записи будем далее полагать /3 = 1, как это делалось в [2] при анализе осцилляций Солнца. Первые два уравнения этой системы эквивалентны уравнениям переноса маркеров и имеют общее решение следующего вида:

Q«)hr = /(£<), Q«)hz = В (£<),

(8.4)

где /■(£, С) и В(£, С) = некоторые функции автомодельных переменных. Подставляя (8.4) в уравнение (8.3), находим, что его общее решение эквивалентно выбору функций /■(£, С) и В(£, С) в таком виде:

дФн   用— дФн

(8-5)

_-

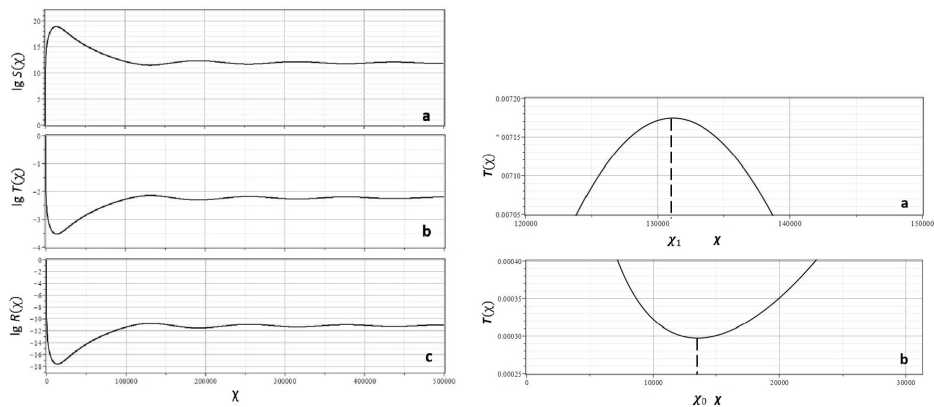
А

В

Рис. 2. Распределение параметров среды для наилучшей модели. (А) Коэффициенты энтропии lg(S) (а), температуры lg( 丁 ) (b) и плотности lg( 冗 )(с); (В) — коэффициент температуры 丁 (х) в двух диапазонах х вблизи нуля

гд ( ? Фя(§<) — произвольная дп ( 1 )( 1 ) ереішпруема.я функция автомодельных переменных.

Предположим, что зональная составляющая магнитного поля 九 尹 либо равна нулю, либо имеет вид:

h_v = a^-2(t^W 怎 Q,

(8.6)

гд ( ? W( §,《)— некоторая не определеііна.я пока (функция. Тогда, подставляя (8.5) в последнее уравнение системы (8.2), приходим к следующему уравнению для Фя ：

дФя ЭУ  дФ н 必          £ (§<)

ае д< = ,     = е

(8-7)

из которого следует, что функция Фн = Фн( §,《 )должна иметь следующий вид:

Фн = F ( V(e,Q ) .

(8-8)

гд ( ? F = F (V) — произвольная ,п;ш] )( ] ) ереші 口 руемая функция, вид которой определяется начальными и граничными условиями. Отсюда окончательно находим:

^{h r} =:^F'(^V)t 也=- 1 ^F'(^V)t

(8-9)

Последние соотношения представляют собой общее решение для магнитного поля звезды, генерируемого совокупным радиальным потоком Хаббла и зональным потоком, связанным с ее автомодельными осцилляциями.

Используя (3.2), можем вычислить компоненты магнитного поля. В соответствии с (3.2) име ем:

^V = е = £ н J / i ^е2 + 几 0(0 .

В результате имеем:

^h 『 =£^F‘(^V) 〃 ‘© ' ^hz= - ±^f' ( ^v ) / 1^е ・

(8.10)

(8.11)

9.    Силовые линии магнитного поля

Уравнения (8.4), (8.5) и (8.7) указывают на то, что векторное поле с компонентами (h_r , h_z ) в каждой плоскости ( 丁, ％ ) является касательным к изолиниям функции У ( £,《 ).Поэтому интегральными линиями поля (h_r , h_z) являются изолинии функции У. В соответствии с этим, соотношения

/ © + / i £ 2 = с

(9.1)

являются уравнениями силовых линий поля (h_r , h_z). Силовые линии, соответствующие (9.1), не являются силовыми линиями магнитного диполя, но при

(9.2)

/ (С) = /і С 2/k + ho, где к — некоторый числовой параметр формы, поле напоминает поле диполя. На рис. 3 представлены силовые линии поля (9.1) для выбора п’(С) в форме (9.2):

С² + к£² = к(О - h o )// i

(9.3)

для двух значений параметра к. Как видно из рисунка, существенное отличие модели от диполя наблюдается вблизи оси вращения. Аналогичная проблема имеется и в модели зонального потока, что отмечалось в работе [2]. Вблизи оси вращения модель требует уточнения.

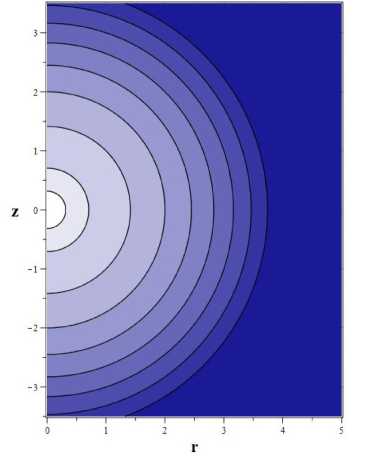
а

Рис. 3. Силовые линии магнитного поля для а) к = 1.0 н b) к = 0.5

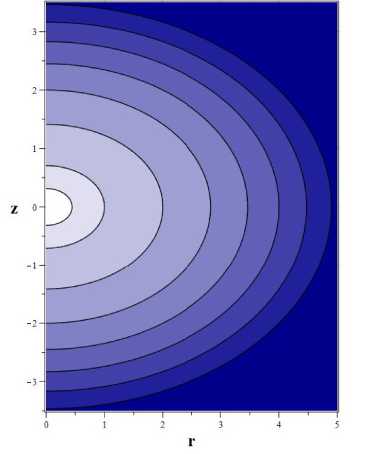
b

10.    Обратное влияние магнитного поля на гидродинамический поток

Соотношения для магнитного поля звезды в динамическом равновесии были получены в предположении, что само магнитное поле мало и не оказывает заметного влияния на гидродинамику. Магнитное поле звезд типа Солнца достаточно слабое, поэтому можно предполагать, что для них обратное влияние не играет существенной роли. Но для более плотных звезд типа белых карликов и нейтронных звезд, магнитное поле которых во много раз превосходит магнитное поле Солнца, обратное влияние может быть существенным.

С этой точки зрения имеет определенный смысл попытаться вычислить влияние магнитного поля на гидродинамический поток. Это можно сделать, если оставить форму гидродинамического потока в исходном виде радиального потока Хаббла вместе с зональной составляющей в виде (2.27). В этом случае уравнения и их решения для магнитного поля остаются неизменными. Исходя из этого, можно вычислить дополнительные силы в (3.1), связанные с воздействием магнитного поля и получить обновленную версию уравнений эволюции масштабного фактора и пространственного распределения температуры и плотности.

Рассмотрим в отдельности последнее слагаемое в правой части уравнения (1.1). После раскрытия векторного произведения для этой составляющей силы находим:

F

- 专 ^VH2 + 靑( H" ) H ・

В покомпонентной форме эти соотношения имеют следующий вид:

Fr

Fz

心

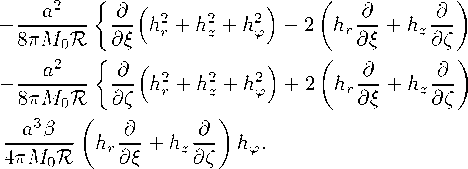
卜

(10-1)

Подставляя в эти соотношения выражения для h_r , h_z ,九 屮 из (8.9) и (8.6), находим:

"-■ ^ 卜⑪ ))23 ^{) 2} + М ) 2) ⁺ J 叫 ⁺4^Ъ (FB ) )² 仆友 -〜^-小 Іри ^{)) 2} (忆^{) 2}+М ^{) 2 )+}《叫^-易(尸支^{)) 2} a di -

\|/7 \|7, ""

f 广以福( FD^{) ) 2} a dl f :) 比                       a 。 2 )

Для того, чтобы структура уравнения для скорости зонального потока 。 не менялась при включении в систему обратного воздействия магнитного поля на поток, достаточно потребовать выполнения условия:

W = N (V), где N(V) — произвольная діі(])(])ереші,ііруемая (функция V. В этом случае последнее уравнение в (10.2) автоматически выполняется. Оставшиеся два уравнения необходимо подставить в уравнения (3.3) и вновь провести разделение переменных.

Для удобства анализа представим (10.2) в следующем виде:

F r = Ui(^,C )+402 仁() ，

Q2

f = Wi ( e,c ) + 4 W2 ( g ， c,                           ( io.3 )

a2

где

^U1= - 1 ： 「 ｛(^{( v ) 2}+м ^{) 2} ).卜 ^n|F ‘ ^{( v} ) | +2ⁱⁿ (^{( v ) 2}+ ^{( V} ) ² )] + ( ^V.^{- V}. ) ^V ｝，

—= - ( ^М ｛^{( ( v ) 2}+ ( ^{v ) 2}). 卜 ⁿ 尸 ( ^v ) | +2¹n ( ( ^{v ) 2}+ ^{( v} ) ²⁾]^- (^v .^{- v} .)^v 卜 1 d                        1 d

% = ^-3両 ^N2^(v )，也=^-…改 ^N2^(v )•                      a° 」)

Используя вычисления (см. Приложение), результатом которых являются соотношения (П.1), и полагая в них к = 1, выражения для Ui и Wi из (10.4) приводятся к такому виду:

Z （ V ） П = -   Z （ V ） е W = - z （ V ） 起 二 - Z （ V ）

4冗GM。冗之   4冗GMoV冗''    1   4冗GM。冗《   4冗GM°V冗 где

N ( V ) M ( V ) . w 二— N ( V ) M ( V ) . 8 冗 M o V 冗 *'    ² —   8 冗 M o V 冗

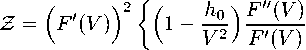
_ 包 _ еh 血 ｝

(10.5)

Следует отметить, что в случае к = 1 функция V = V(£, 《 )оказывается функцией переменной 〃 ² = £ 2 + С2. Такая ситуатпія в качестве нулевого приближения рассматривалась в [2] для распределения плотности и температуры среды. Поэтому условие к = 1 не меняет выводов модели без магнитного поля и в случае его наличия, по крайней мере в нулевом порядке. Учитывая, что Ғ(V) ii N (V) произвольны, можно установить условия, при которых ра ， зде, 「 етше переменных в уравнениях (3.3) с дополнительными силами (10.3) останется без особых изменений. Для этого достаточно потребовать, чтобы выполнялись дополнительно к (4.1) два условия:

Z (V)      г

-----------=厶 1 = const ,

4 冗 GM o V 冗    ¹      ,

N ( V ) N ‘ ( V ) 8tM ° V 冗

丄 2 = Const .

(10.6)

Параметр 丄 i характеризует воздействие магнитного поля на радиальный ii вертикальный потоки, а 丄 2 — на ^зональный. Знаки этих параметров могут с (формальной точки ^зрения быть лтобыми.

Из условий (10.6) вычисляются функции Ғ(V) и N(V). При выполнении этих условий уравнения эволюции масштабного фактора будут иметь такой вид:

Q _ 〃 Q 3 _ (“ _ 丄 2 )0 ， 2 + 丄 i = 0.

А уравнения распределения коэффициента температуры останутся неизменными.

11.    Уравнения эволюции в магнитном поле

Проводя обезразмеривание этого уравнения в соответствии с (5.3) и полагая при этом:

〃 3 / 2

0 0 = n/1" _ 厶卜力 0 =

1 〃 - 厶| ²

уравнение (10.7) будет выглядеть так:

д = X 3 + X 2 _R ， х = д.

(10.7)

(П.1)

(П-2)

Здесь s = sign( “ _ 丄 2) = signA hr = 丄 i 力 0 /。°. Пара метр r будем называть параметром полоид альной структуры магнитного поля, поскольку он соответствует именно той части силового воздействия магнитного поля на гидродинамический поток, который определяется компонентами поля h_r и 九乞. Интеграл энергии этого уравнения имеет следующий вид:

д2     1     1

(П-З)

万+ s 扇+五 2 + 叫, =凡

Динамическая система (11.2) имеет в зависимости от параметров s = ±1 и r одну или две особых точки. Все точки на фазовой плоскости х, д располагаются на оси абсцисс д = 0, координаты которых вычисляются из решения уравнения:

X 3 +

s

—_ R = 0.

X2

(П.4)

Корни этого уравнения имеют такой вид:

X (р)     2s

^Xi = " + Х(р), ^X2 , ³

- ； x i ( p ) ± Т '

.

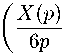
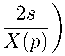
Здесь:

X (p)= (12 孤 75 而 +108 ) 1/3 *3, D =型产 .

Анализ расположения корней удобно проводить в графическом виде. На рис. 4 представлено графическое решение уравнения (11.4). Координаты точек пересечения красной (s = 1) и фиолетовой (б = —1) линий с кубической параболой (обозначена синим цветом) для различных значений параметра w соответствуют особым точкам системы (11.2). В случае s = 1 в положительной области значений т устойчивых особых точек, что соответствует отсутствию пульсаций. Как видно из графиков, в случае s = —1 (А < 0) в положительной области нормированного масштабного параметра т имеются либо одна, либо две особые точки w < 0. В случае w > 0 имеется только одна особая точка, которая является центром. В случае w < 0 имеется область значений параметра w, когда в системе имеются две особые точки. Одна из точек является центром, а вторая - седловой точкой. Из графиков видно, что область значений параметра w, для которых существуют две особые точки, является достаточно узкой. Соответствующие фазовые портреты представлены на рис. 5.

На рис. 5a представлены фазовые портреты для w = 0.05, а на 5 b — для w = —0.05. Основным отличием фазовых портретов пульсаций без обратного влияния магнитного поля (рис. 1) от портретов на рис. 5 при s = —1 и w > 0 является то, что при увеличении энергии колебаний Е т х система остается устойчивой. В случае же s = —1 и w < 0 при увеличении энергии после достижения Е t —0.41845 система перестает быть устойчивой и при 力 т х расширяется с ускорением, что соответствует взрыву звезды. Это означает, что при w > 0 магнитное поле стабилизирует звезду, а ， при w < 0 суттіествует небольшая область стабильности вблизи значения Е t —0.5.

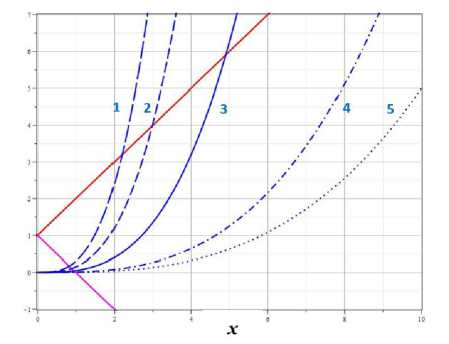
а

Рис. 4. Графическое решение задачи об особых точках динамической системы (11.2). а) в > 0: 1 -си = 0.3, 2 - в = 0.15, 3 - в = 0.05, 4 - в = 0.01, 5- в = 0.005; b) в < 0: 1 - в = -0.3, 2 - в = -0.15, 3 -в = -0.05, 4 - в = -0.01, 5- в = -0.005

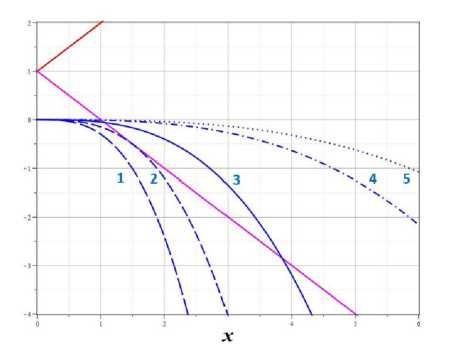
b

Для более детального анализа эволюции звезды с магнитным полем требуется привлечение реальных данных о конкретных звездах, что выходит за рамки данной работы.

Заключение

В работе построена общая модель магнитного поля звезд, находящихся в динамическом равновесии, на основе математического аппарата, развитого в работе [2]. Важным является то, что магнитное поле не меняет формы модифицированных уравнений Лейна-Эмдена, но меняет значения некоторых ее параметров, в частности, параметра динамического равновесия. Магнитное поле звезд в рамках такого подхода органически связано с самой моделью эволюции, в том числе, пульсациями звезд. Как было показано в работе, форма силовых линий магнитного поля звезды

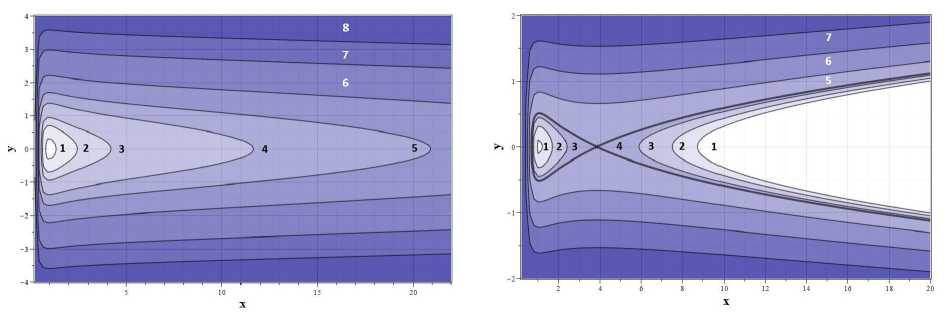
а

b

Рис. 5. Фазовые портреты динамической системы (11.2). а) з > 0: 1 - Е = —0.4, 2 - Е = —0.2, 3 - Е = 0, 4 - Е = 0.5, 5- Е = 1.0, 6- Е = 2.0, 7- Е = 4.0, 8- Е = 6.0; b) з < 0: 1 - Е = —0.545, 2 - Е = —0.5, 3 -Е = —0.45. 4 - Е = —0.41845 (сепаратриса). 5- Е = —02 (і- Е = 02 7- Е = 0.75

пульсирует вместе с общей структурой звезды и остается неизменной в автомодельных переменных. Магнитное поле звезды не имеет точной формы магнитного диполя, но вдали от оси вращения близка к ней. Как и в исходной модели эволюции звезды [2], вблизи оси вращения имеются особенности в магнитном поле на оси вращения звезды, которые и делают поле, отличным от поля магнитного диполя.

В случае сильного магнитного поля, оказывающего влияние на гидродинамические потоки, уравнения эволюции звезды со слабым магнитным полем дополняются слагаемым, обусловленным полоидальной частью магнитного поля. Это приводит к возникновению дополнительных режимов в модели осцилляций звезд и при изменении знака параметра полоидальной структуры 归 изменяет их общий характер. При х > 0 пульсации звезд не исчезают ни при какой энергии колебаний Е и при любых начальных условиях. При х < 0 осцилляции возможны лишь в узком диапазоне значений энергии, и звезда переходит в режим неограниченного расширения при превышении некоторого предельного значения энергии Е. В работе проведен лишь общий анализ полученных уравнений эволюции, а также качественный их анализ. Более детальный анализ для конкретного типа звезд требует привлечения конкретных экспериментальных данных, что выходит за рамки данной работы.

Работа выполнена в рамках проекта 0777-2020-0018, финансируемого из средств государственного задания победителям конкурса научных лабораторий образовательных организаций высшего образования, подведомственных Минобрнауки России и частично в рамках проекта РФФИ 20-0200280.

Приложение

Вычислим в явном виде компоненты сил, связанных с магнитным потоком. Используя (8.10) и (9.3), вычисляем функцию V 二 V ( £,《):

V 二 Е н q o VС ²/к + ^ 2 + h o /f i , q o 二 УЛ.

Отсюда:

dV — Ен q o        dV

К 一灰— К 一灰

^Ен qo _А 「《.

Из этих соотношений следует:

(") 2 + (起 ) 2 = 膚(产 + C²/* )=:( V² - % +, 2 (1 - 灯 /* )，

& ^ i д 卜 = 翠％ ,                  ⑴⑴

& \ д N = - 要%.