Магнитные свойства мелкодисперсного НЯП в парамагнитном состоянии

Оксиды с размерами частиц от нескольких единиц до сотен нанометров обладает рядом уникальных физико-химических свойств, обусловленных сильноразвитой поверхностью и специфическим состоянием приповерхностного слоя кристаллов [1]. Оксид никеля широко применяется как катализатор многих гетерогенных реакций или в качестве составляющего многокомпонентных систем. В мелкодисперсном состоянии кристаллическая решетка оксида никеля характеризуются различными структурными формами - от кубической до ромбоэдрической кристаллической структуры [2]. Обладая атомным антиферромагнитным порядком, данный оксид относится к группе магнитных полупроводников, имеющих большое практическое значение [3].

Физико-химические свойства крупнодисперсного NiO известны и подробно описаны [4]. Измерение теплоемкости оксида показало, что температура фазового перехода из антиферромагнитного в парамагнитное состояние равна 247 °C. При данной температуре происходит перестройка кристаллической решетки из тригональной в кубическую. В отличие от других оксидов многочисленные измерения магнитной восприимчивости NiO не позволяют точно определить температуру Неля, а в парамагнитной области NiO обладает аномальными магнитными свойствами, удовлетворительное объяснение этого явления отсутствует [3^4].

Цель данной работы - изучение магнитных свойств мелкодисперсного NiO в парамагнитной области.

Экспериментальная часть

Деференциально- термический анализ основного карбоната никеля проводили на деривато-графе типа Paulik. По данным ДТА разложение основного карбоната никеля начинается с 330 и полностью заканчивается при 380 °C. В связи с этим оксиды NiO получали изотермическим разложением на воздухе основного карбоната марки ОСЧ при температурах 380, 430, 480, 530, 580, 600, 700 и 800 °C в течение 3 часов. Средний размер кристаллов NiO после прокаливания определяли по ширине рентгеновских дифракционных максимумов на дефрактометре ДРОН ЗМ Си К_а излучение по формуле Селякова [5]. Электронно-микроскопические исследования проводили на электронном микроскопе ПМ-100 и Электронно-сканирующем микроскопе JOEL 2000.Удельную поверхность измеряли методом БЭТ по тепловой абсорбции аргона. Магнитную восприимчивость %, как и в работе [6], измеряли методом Фарадея в температурном интервале 20-650 °C. Относительная систематическая ошибка в измерениях / не превышала 3 %.

Обсуждение результатов

Порошки оксида никеля после прокаливания от 380 до 580 °C имели черный цвет, с повышением температуры прокаливания до 800 °C образцы приобретали серо-зеленый цвет. Яркозеленый цвет NiO приобретал при более длительном прокаливании при 800 °C (100 час).

В табл. 1 представлены размеры кристаллов оксида никеля после прокаливания рассчитанных по формуле Селикова и их средний размер по данным электронной микроскопии, а также их удельная поверхность, измеренная методом БЭТ и рассчитанная в приближении сферических частиц NiO.

Таблица 1

Размеры кристаллов (R) и удельная поверхность (8_УД) оксида никеля после прокаливания основного карбоната

	Расчетные данные по рентгеновским пикам		Данные, полученные с микроскопа и БЭТ
Т °C	/?, А	SNa, м2/г	7?, А	'Зуд» М /г
380	44,8	89,80	25-35	250
430	57,3	70,25	41-57	210
480	86,2	46,73	132-144	70
530	109,2	36,86	173-176	50
580	109,2	36,86	210-405	30

Отметим, что средний размер кристаллов, рассчитанный по ширине рентгеновского пика совпадает с данными электронной микроскопии, однако величина удельной поверхности измеренная методом БЭТ значительно выше рассчитанной, что, по-видимому, связано с пористой структурой образцов прокаленных при температурах 380 и 430 °C. Пористая структура последних образцов хорошо видна на снимках с электронно-сканирующего микроскопа.

1-а                               1-6

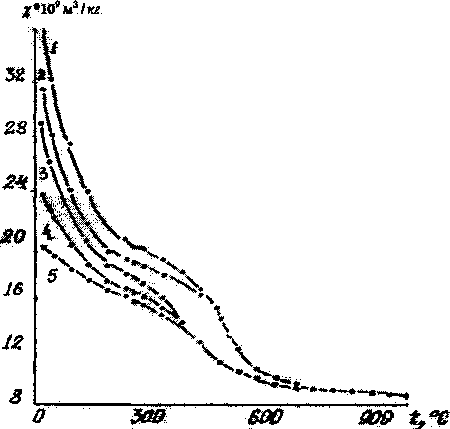
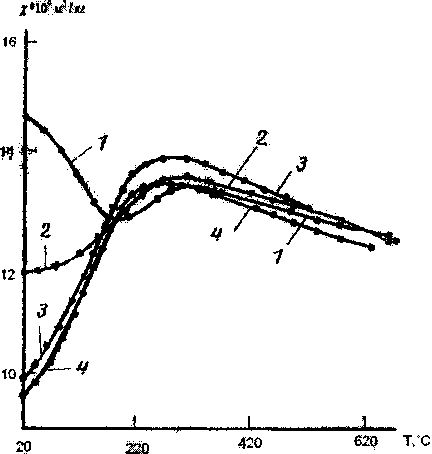
Рис. 1. Температурная зависимость магнитной восприимчивости мелкодисперсных оксидов никеля от температуры прокаливания: а) 1- 380 °C, 2 - 430 °C., 3 - 480 °C, 4 - 530 °C, 5 - 580 °C 6) 1- 600 °C, 2 - 700 °C, 3 - 800 °C (3 часа), 4 - 800 °C (100 часов)

На рис. 1 представлены зависимости / от температуры измерения Т_и в интервале 25-900 °C. Отметим, что эти зависимости существенно различны для образцов прокаленных до 600 (рис. 1-а) и после 600 °C (рис. 1-6).

Характерная антиферромагнитная зависимость / от Ги наблюдаются только для образцов прокаленных после 600 °C. Отметим что, магнитная восприимчивость мелкодисперсного оксида никеля полученного прокаливанием до 600 °C изменяется не монотонно с температурой, зависит от размеров кристаллов и имеет несвойственный для антиферромагнетиков вид. Для этих образцов/-температура измерения и/-температура охлаждения различны, что указывает на активное спекание кристалликов NiO. Для прокаленных выше 600 °C эти значения в пределах ошибки измерения совпадали.

Аппроксимацию экспериментально наблюдаемых зависимостей магнитной восприимчивости от температуры по уравнению Кюри-Вейсса выше температуры Нееля проводили методом наименьших квадратов. Полученные данные представлены в табл. 2.

Z ЗЦТ + ®У где N - количество ионов Ni2+, /?эфф - эффективный магнитный момент Ni2+, который определяется по формуле спина: /)эфф =^[^s(sVY), спин катиона Ni2+ 5=1,0- аппроксимационная постоянная Кюри-Вейсса, к - постоянная Больцмана, Р - магнетон Бора, s - суммарный спин.

Таблица 2

Аппроксимационные параметры зависимостей х= АЛ по уравнению Кюри-Вейсса для образцов ЫЮ, полученных термолизом основного карбоната (г - время термолиза)

Т °C	т, час	Р*	0	g
380	3	2,32	4,3	1,64
430	3	2,32	7,28	1,64
480	3	2,32	17,34	1,64
530	3	2,65	221	1,87
580	3	3,53	727	2,5
600	3	6,71	5050	4,74
700	3	6,15	4100	4,35
800	3	5,61	3363	3,97
800	100	5,29	2800	3,74

Следует обратить внимание, что для образцов прокаленных в температурном интервале 380580 °C значение эффективных магнитных моментов, а также g-фактор катионов Ni²⁺ близки к чисто спиновому. Для образцов прокаленных выше 580 °C значение этих величин значительно больше рассчитанных по формуле спина, что нельзя объяснить с позиции классической теории парамагнетизма. Некоторые авторы предлагают ввести поправку на эффекты не зависящего от температуры парамагнетизма, что может значительно снизить />_эфф и 0 [7]. В работе [6] был произведен оценочный расчет этой поправки, показано, что значение ее не согласуется с литературными данными для полупроводников, каким является оксид никеля. Поэтому аппроксимацию эксперементально наблюдаемых зависимостей / от Т_И проводили по модели Гейзенберга-Дирака-Ван-Флека (ГДВФ) в приближение двух и четырех взаимодействующих катионов.

В модели ГДВФ энергия взаимодействия ионов определяется уравнением

Е = -j[s^z (У +1) - 2s(s +1)] + D^s' -\l3s\s¹ -1)],                 (2)

где J - параметр обменного взаимодействия между катионами Ni²⁺, D - параметр расщепления энергетических уровней в нулевом поле, У - суммарный спин взаимодействующих ионов, M_s = У; 5-1;...—s^z - проекция суммарного спина.

В приближение парного обменного взаимодействия магнитная восприимчивость описывается уравнением

Np² г.         1 + х²(1 + 4у³)

/ =——g Зху ---------(3)

ЗкТ      1 + х(1 + 2у) + х³(1 + 2у + 2/)

где g - фактор спектроскопического расщепления, у = ехр(-Г>/к7), х = exp(2J + 2DI3)IkT. Зависимость / от Т_И в приближение четырех взаимодействующих ионов имеет вид:

^2 2        х’°(16у’6+9у9 +4/ +у) + 3х6(9/ +4/ + у) +

ЗкТ ⁸   ’   1.5 + х¹⁰(у¹⁶ + у⁹ + у⁴ + у+ 0.5)+ 3х⁶ (у⁹ + у⁴ + у + 0.5) +

+6х³(4у⁴+у) + 6ху +6х³(/ +0,5) + 6х(у + 0,5)

По данным [8] значение D для NiO заключено в пределах - 30 до 30 К. Знак определяет направление деформации элементарной ячейки NiO.

В табл. 3 представлены параметры g и J, соответствующие максимальному коэффициенту корреляции для уравнений (3) и (4). Анализ данных табл. 3 показывает, что коэффициенты корреляции. рассчитанные по модели ГДВФ выше чем по уравнению Кюри-Вейсса. При увеличении количества взаимодействующих катионов в модели в 2 раза обменное взаимодействие между ка-

Химия_______________________________________________ тионами уменьшается также приблизительно в 2 раза, однако g-фактор Ni2+ возрастает. В [8] указывается, что экспериментальная величина g-фактора катиона Ni2+ не превышает 2,50. таким образом, наиболее вероятно, что зависимость х от Т для NiO в парамагнитной области описывается уравнением (3).

Таблица 3 Аппроксимационные параметры уравнений (3) и (4) для образцов NiO, полученных термолизом основного карбоната

Д °C	т, ч	Уравнение	£> = 0,К			£> = -30, К			D = 30, К
			J	g	R	J	g	R	J	g	R
600	3	(3) (4)	-310 -140	2,51 2,64	0.941 0,951	-310 -150	2,46 2,61	0,944 0,946	-300 -135	2,51 2,66	0,951 0,953
700	3	(3) (4)	-300 -135	2,48 2,60	0,968 0,975	-300 -145	2,43 2,58	0,969 0,972	-290 -125	2,49 2,63	0,975 0,976
800	3	(3) (4)	-280 -125	2,39 2,54	0,985 0,988	-280 -135	2,38 2,51	0,981 0,988	-270 -115	2,40 2,57	0,986 0,988
800	100	(3) (4)	-270 -130	2,39 2,54	0,986 0,980	280 -140	2,34 2,51	0,983 0,979	-260 -120	2,40 2,56	0,985 0,981

Выводы

Методом магнетохимического анализа исследовали магнитные свойства NiO, полученного термолизом основного карбоната никеля.

Показано, что магнитная восприимчивость образцов прокаленных при Т ^ 600 °C не монотонно изменяется от температуры Т_и и обладают суперантиферомагнетизмом. У образцов термообработанных выше 600 °C наблюдается лямдообразная зависимость магнитной восприимчивости от температуры.

Математическая обработка результатов показала, что экспериментальные зависимости х ^от Т_и в парамагнитной области описываются не законом Кюри-Вейсса, классическим для антиферромагнетиков, а уравнением, полученным в рамках модели Гейзенберга-Дирака-Ван-Флека в приближении парного обменного взаимодействия.

В связи с этим предполагается, что в парамагнитной области локально между катионами никеля в NiO сохраняются достаточно сильные обменные взаимодействия. Оценены значения g-факторов и параметры обменного взаимодействия Ni2+-Ni2+ в NiO с учетом расщепления энергетических уровней в нулевом поле.

Работа выполнена при поддержке ректора ЧГПУ Латюшина В .В.