Магнитостатические волны в зазоре продольно намагниченных ферромагнетиков с относительным продольным перемещением

Во всех работах, в которых рассматривались щелевые магнитостатические волны, всегда полагалось, что ферромагнитные кристаллы статичны [1; 2]. Для оценки новых перспективных приложений активных (пьезоэлектрических или магнитных) материалов в робототехнике и ме-ханотронике, в устройствах которых нередко реализуется движение механически неконтактных деталей конструкций, актуально изучение волновых процессов в щелевых структурах при наличии относительного продольного перемещения (ОПП) составляющих их сред.

Сравнительно недавно были опубликованы работы [3; 4], в которых обсуждалась возможность проявления в магнитоупорядочных средах аномального эффекта Доплера, характерного для искусственных метасред [5; 6]. В частности, в [3] сообщалось об экспериментальном наблюдении аномального эффекта Доплера при распространении обратных объемных магнитостатических волн в свободной ферромагнитной пленке, намагниченной в направлении распространения магнитостатических волн (МСВ) (продольное намагничивание). Исследовались также прямые поверхностные МСВ (поперечное намаг- ничение1), для которых направления фазовой и групповой скорости совпадают. При этом было установлено, что для поверхностных МСВ эффект Доплера является нормальным.

В [4] теоретически обосновано предположение о существовании аномального эффекта Доплера для магнитостатических волн в ферромагнитных пленках. Ранее подобные доплеровские преобразования спектров рассматривалось для элект-розвуковых волн в планарной щелевой структуре пары пьезоэлектриков, испытывающих относительное продольное перемещение (ОПП) [7] .

Недавно в [8] аналогично работе [7] нами рассматривалось проявление ОПП для магнитостатических волн в поперечно намагниченных ферромагнитных кристаллах со щелью, усложненное из-за резонансного отклика и частотной дисперсии сред. Было показано, что в такой структуре возможно распространение симметричной (прямая МСВ) и антисимметричной (обратная МСВ) мод. При этом как для обратной, так и прямой МСВ имеет место увеличение частоты в системе покоя одного из кристаллов (в котором мы мысленно располагаем приемную антенну), если направление фазовой скорости

МСВ и направление ОПП противоположны. Таким образом, эффект Доплера в структуре при поперечном намагничивании сред для обеих мод оказывается нормальным.

В данной работе впервые рассмотрены щелевые МСВ в зазоре продольно намагниченных ферромагнетиков с ОПП. Из анализа спектра определен тип щелевых мод МСВ, а также установлен знак смещения частот мод вследствие ОПП.

1. Постановка задачи и исходные уравнения

На рис. 1 показана геометрия задачи. Два по-лубесконечных ферромагнитных кристалла с одинаковой намагниченностью М о( j ) вдоль оси х ( М 0(1) ТТ М 0(2) И [100], j = 1, 2, где j — номер среды) разделены диэлектрическим зазором 2h . Магнитная проницаемость большинства диэлектриков мало отличается от единицы, поэтому в дальнейшем магнитную проницаемость зазора мы в расчет не принимаем.

Далее предположим, что вторая пленка ( j = 2) движется параллельно первой вдоль оси х со скоростью V . Внутреннее магнитное поля H i в кристаллах, в которое входит поле анизотропии также направлено вдоль оси х . Условимся, что щелевые магнитостатические волны (ЩМСВ), распространяющиеся в зазоре и в пленках вдоль оси х с волновым вектором k = ( k , 0, 0), описываются в безобменном магнитостатическом приближении.

Решение строим в лабораторной системе отсчета х 0 yz , привязанной к неподвижной среде ( j = 1, y <  h ). Однако параметры волн, возникающих в движущейся среде ( j = 2, - h <  y ), соотнесем с попутной системой отсчета X 0 yz , привязанной к движущейся среде. Из-за автоматически выполняющегося неравенства V << с , где с —

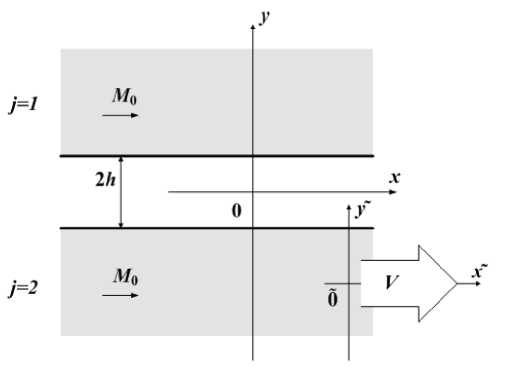
Рис. 1. Геометрия задачи. Ферромагнитные пленки выделены серым фоном. Большой стрелкой показано направление движения второй пленки со скоростью V

скорость света, связь координат систем отсчета двух пленок будет определяться преобразованием Галилея. В итоге волны в движущейся среде получат частотный сдвиг Q = to - kV , где to — частота волны в лабораторной системе отсчета.

Магнитные потенциалы ф j в оговоренных условиях распространения магнитостатических волн удовлетворяют уравнению Уокера [9] в ферромагнетике и уравнению Лапласа в диэлектри-

ческом зазоре:

Ц j

d^i

2 ^д У

^д Ф j + ₂

д х

=0,

где F 1 ‘, F 2', C , D — амплитуды поверхностных магнитостатических колебаний. Согласно (2), коэффициент локализации МСВ в первом и втором ферромагнитном кристалле определяется в виде q 1,2 = ^k / 7^1,2 .

Граничные условия для нашей задачи выразятся непрерывностью магнитного потенциала и непрерывностью нормальной компоненты магнитной индукции на границах щелевой структуры y = h , у = - h :

^b y ^{1 b} y ⁰ l y = h ’    b y ^{2 b} y ⁰ l y =- h ’

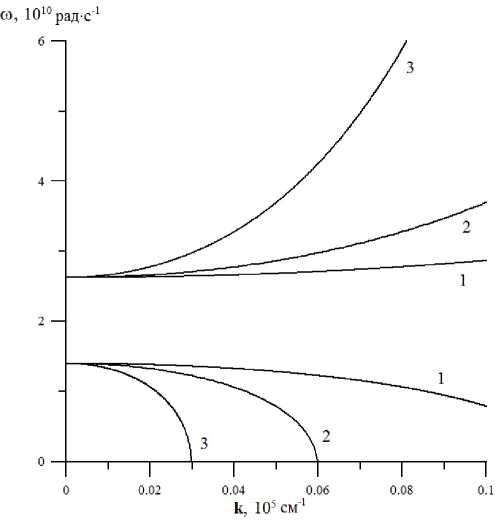
Рис. 2. Спектр щелевых МСВ при различной ширине зазора 2 h между кристаллами и V = 0. Кривая линия 1 – h = 0.5 ⋅ 10 - ⁴ см, кривая линия 2 – h = 10 - ⁴ см, кривая ли ния 3 – h = 2 ⋅ 10 - ⁴ см

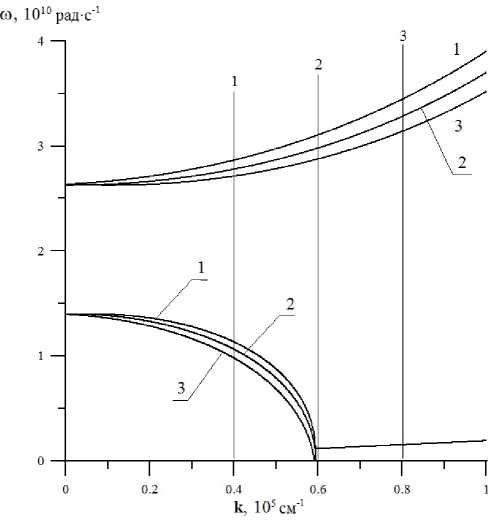
Рис. 3. Спектр щелевых МСВ при учете скорости движения второго кристалла; ширина зазора h = 10 - ⁵ см. Кривая линия 2 – V = 0, кривая линия 3 – V = 0.1 c_t , кривая линия 2 – V = - 0.1 c_t

ϕ ₁ = ϕ _{0 y = h} , ϕ 2 =ϕ 0 y =- h ^,

где

∂ϕ ₁

b _{y 1} = -µ ₁      ,

∂ y

b

∂ϕ 2

_{y 2} = -µ ₂ ∂ y

Знаки перед экспонентой « ± » в (8) показывают, что в щелевой структуре двух ферромагнетиков с продольной намагниченностью, аналогично случаю поперечного намагничивания ферромагнетиков [8], существуют две моды щелевых МСВ.

b y 0 =

∂ϕ ₀ ∂ y ^,

Подставляя решения (3) в граничные условия (4), получим систему из четырех алгебраических уравнений относительно четырех неизвестных F ₁ ′, F ₂ ′ , C , D .

Из условия разрешимости этой системы получим дисперсионное соотношение для щелевых МСВ, распространяющихся в зазоре между двумя продольно намагниченными ферромагнитными кристаллами:

3. Спектры щелевых магнитостатических волн

Прежде чем анализировать влияние движения одного из кристаллов на спектр щелевых МСВ,

рассмотрим влияние параметров структуры на дисперсионные свойства МСВ в отсутствие ОПП. Рассчитанные дисперсионные зависимости для различной толщины зазора, согласно формулам (7), (8), показаны на рис. 2. Расчеты этого

th(2 kh ) = ⁽ µ¹ + µ²⁾. (1 + µ 1 µ 2 )

В отсутствие движения при V = 0 дисперсионное соотношение имеет более простой вид:

и последующих рисунков выполнены для кристаллов железоиттриевого граната с параметрами ω ₀ = 1.4 ⋅ 10¹⁰ рад ⋅ с - ¹, ω _m = 3.5 ⋅ 10¹⁰ рад ⋅ с - ¹, ω _k =2.62⋅10¹⁰ рад⋅с - ¹.

Согласно рис. 2, зарождение кривых спектра происходит на частотах ω ₀ и ω _k . При этом

ω=

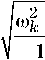
- a ω ₀

- a

высокочастотная ветвь существует во всем диапазоне волновых числах k , тогда как низкочас-

где a = (± exp(-2kh) - 1)2 (± exp(-2kh) + 1)2

тотная ветвь, зарождение которой происходит на частоте ω ₀ , имеет точку обрезания спектра k ^*. Волновое число k ^* определяется, согласно (7),

(8), выражением

k ^*

Arcch	Г-	■        1
		to k - to 0

h

согласно которому, при h ^ 0 и к ^ ю, что подтверждает ход дисперсионных кривых на рис. 2. При h ^ 0 дисперсионные кривые асимптотически выходят на уровни частот tog и to к, причем в безграничной среде возможна лишь одна ветвь с частотой to = tok, соответствующей частоте однородной прецессии магнитных моментов [9]. При h ^ ю (полубесконечная среда) решение отсутствует, поскольку граница ферромагнетик- диэлектрик при продольном намагничивании ферромагнетика не допускает распространения поверхностной МСВ.

На рис. 3 показан спектр ЩМСВ с учетом относительного продольного перемещения второго кристалла для фиксированного значения ширины зазора h = 10 5 см. Для нормировки скорости ОПП использовано значение скорости акустических поперечных волн с£ = 3.8 ■ 105 см/с в ЖИГе. В целом модификация спектров магнитостатических волн в щелевой структуре ферромагнитных кристаллов за счет ОПП (рис. 3) аналогична модификации спектра щелевых магнитостатических волн в зазоре ферромагнетиков при поперечном намагничивании кристаллов [8].

При V >0 (сонаправленное распространение волн относительно движения кристаллов) кривые спектра разворачиваются в высокочастотную (см. штриховые кривые на рис. 3), а при V < 0 — наоборот, в низкочастотную область (см. утолщенные кривые на рис. 3). С обращением скорости ОПП преобразование спектров происходит так, как если бы каждый спектр магнитостатической волны соответствующей симметрии расщеплялся на две ветви. Такое расщепление носит невзаимный характер, отражая известную невзаимность свойств магнетиков в резо- нансных условиях.

Учет ОПП также приводит к смещению точки *

k нижней ветви, определяемой из трансцендентного уравнения:

* 1 ch( к h ) = —

I4 to k - к *² V ² v ^to k ^{- to} 2

и может быть рассчитано только численно. Ха *

рактерно, что в точке к (при V > 0) происходит изменение типа дисперсии (с аномальной на нормальную) для квазисимметричной моды. Как показано в [10], учет затухания позволяет заменить резкий углоообразный излом спектра в точке k* точкой перегиба, в которой выполняется условие экстремума групповой скорости d2to / д2к = 0. Такую точку в теории волноводных систем называют точкой нулевой дисперсии. Для нее характерно минимальное уширение импульсов волн при распространении по волноводу и, следовательно, минимальное искажение информационной полосы пропускания волноводной структуры [11].

Как видно из рис. 3, можно значительно изменить фазовую скорость ЩМСВ, варьируя скорость перемещения движущегося кристалла. При этом в области больших волновых чисел можно «разогнать» симметричную моду при V >  0 (для к = 2 ■ 10 4 см изменение фазовой скорости составляет примерно 20 ^) или сильно «замедлить» антисимметричную моду по сравнению с фазовой скоростью ЩМСВ для статичной структуры. Такая «добавка» к фазовой скорости ЩМСВ возможна, но только при достаточно больших скоростях ОПП, составляющих десятые доли скорости звука. Скорости поступательного движения такой величины трудно достичь на практике, но можно предположить, что при других конструктивных реализациях ОПП, например при вращениях или колебаниях кристаллов относительно друг друга с большой частотой, соответствующие эффекты окажутся доступными для наблюдения. Минимальную скорость ОПП V _MUH , доступную измерению в эксперименте, можно оценить, если воспользоваться для этого минимальной величиной разрешения по частоте спектральных линий магнитостатических волн Ato/to ~ 10 ^{- 6} [3]. В нашем случае Ato — это доплеровский сдвиг частоты щелевой МСВ в результате движения кристалла, определяемый величиной Vk . Подразумевается, что мы измеряем частоту волны в движущемся кристалле, а затем сравниваем ее с частотой в лабораторной системе отсчета. Для волнового числа к = 2 ■ 10 4 см и частоты to ® 5 ■ 10 9 с получим значение V _MHH ~ 0.2 см/с. Если считать, что Ato — это изменение частоты моды щелевой МСВ в спектрах рис. 3 для выскочастотной Ato 5 (низкочастотной Ato a ) ветви в результате ОПП, то в качестве to естественно рассматривать частоту щелевой МСВ в статичной структуре ферромагнетиков со щелью. В таком случае численная оценка для спектров с параметрами рис. 3 дает значение V _MUH как высокочастотной, так и низкочастотной мод приблизительно порядка нескольких сантиметров в секунду.

у, Ю4см

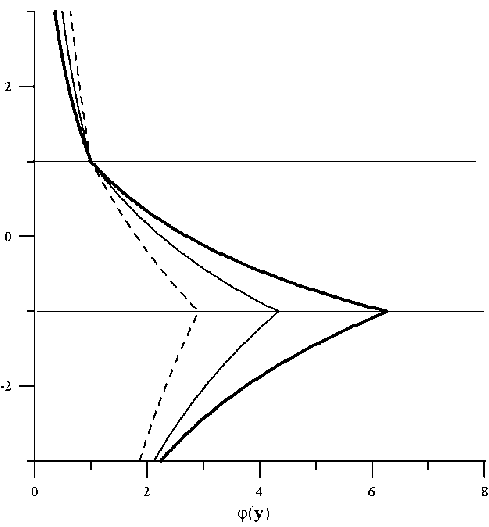
Рис. 4. Профиль распределения магнитного поля ЩМСВ нижней ветви спектра рис. 3 при h = 10 - 5 см и V = 0 для ряда значений волнового числа: штриховая линия — к = 0.4 ■ 10 5 см ^{- 1}, тонкая сплошная линия — к = 0.6 ■ 10 5 см ^{- 1}, утолщенная линия — к * = 0.8 ■ 10 5 см ¹

У, Ю4см

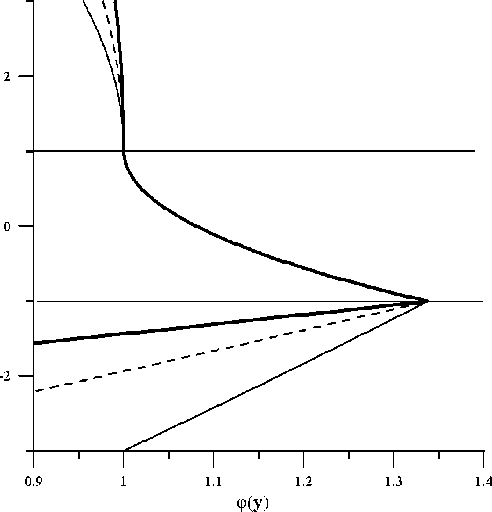
Рис. 5. Профиль распределения магнитного поля ЩМСВ высокочастотной ветви спектра рис. 3 при к = 0.4 ■ 10 5 см ^{- 1}, h = 10 ^{- 5} см для ряда значений скорости ОПП: штриховая линия — V = 0, тонкая сплошная линия — V = 0.1 c , утолщенная линия — V = - 0.1 C t

Приведем сравнение доплеровского сдвига частот с доплеровским сдвигом магнитостатических волн в пленке, подмагниченной по направлению распространения волны [3]2. В эксперименте, описанном в статье [3], двигался не сам кристалл, а приемная антенна. Согласно экспериментальным измерениям для скорости движения приемной антенны 90 см/с (240 оборотов в минуту), частоты МСВ 3 ГГц, волнового числа к ~ 34 см 1, доплеровский сдвиг частоты магнитостатической волны составил 500 Гц. Расчетные значения для нашей модели ЩМСВ: V = 90 см/с, к = 34 см-1 и на частоте мод to ® 4.2 ГГц, доплеровские приращения для высокочастотной и низкочастотной мод составили Ato 5 ® 243.1 Гц, Ato a ® 244.4 Гц, обеспечивая равенство Ato a + Ato 5 ® Vk. Из их сравнения можно сделать вывод о совпадении по порядку величины экспериментальных данных [3] с расчетными значениями для щелевых волн. Как для обратной, так и прямой ЩМСВ в системе покоя кристалла с мысленно распо- ложенной антенной происходит увеличение частоты, если направление фазовой скорости МСВ и направление ОПП противоположны. Таким образом, эффект Доплера в щелевой структуре с продольным намагничиванием сред для обеих мод является нормальным.

Отметим, что результирующий доплеровский сдвиг на два порядка выше, чем для электромагнитной волны той же самой частоты. Указанная «сверхчувствительность» магнитостатических волн к движению приемного устройства или самого активного кристалла, вытекающая из малости скорости распространения магнитостатических волн по сравнению с электромагнитными волнами, напрашивается на практическое использование в устройствах, частотный выход которых совмещен с ОПП.

• 4 . Профили распределения магнитного поля в щелевой структуре двух ферромагнитных кристаллов при ОПП

Для расчета профиля распределения величины магнитного потенциала в такой щелевой структуре воспользуемся системой алгебраических уравнений, полученной ранее для вывода дисперсионного соотношения (6). Затем, отбирая любые 3 из 4 уравнений системы и принимая одну из амплитуд (например, Е{) за единицу, можем выразить через нее все остальные амплитуды. Далее, подставляя полученные выражения в (3), с учетом решений уравнения (6) находим искомые профили полей ЩМСВ распространяющихся в такой структуре. Рассчитанные так профили распределения величины магнитного потенциала для высокочастотной и низкочастотной моды показаны на рис. 4, 5. Расчеты проведены для частот и волновых чисел (показаны тонкими линиями 1, 2, 3 на спектре рис. 3).

Из картины профилей рис. 4, 5 видно, что низкочастотной и высокочастотной моде не соответствует симметричному или антисемметрич-ному распределению магнитного поля в зазоре двух ферромагнетиков. Модификация профиля низкочастотной моды вследствие ОПП аналогична модификации профиля высокочастотной моды (см. рис. 5), но происходит в настолько малых масштабах изменения амплитуд, что изменения профиля низкочастотной моды под влиянием ОПП практически не ощущаются вплоть до скоростей V порядка скорости звука в ферромагнетике. Поэтому на рис. 4 графики профиля низкочастотной моды показаны для разных значений волнового числа без учета влияния ОПП. Как видно из рис. 4, увеличение k приводит к увеличению амплитуды потенциала профиля низкочастотной моды ЩМСВ в зазоре. Причем для k ^*, когда происходит резкое изменение типа дисперсии низкочастотной моды, вид профиля волны остается аналогичным профилю любого другого диапазона волновых чисел.

На рис. 5 тонкими штриховыми кривыми показаны профили магнитного поля высокочастотной моды для статичного случая V = 0, тонкими сплошными кривыми – профили для скорости ОПП V = 0.1ct, а утолщенными сплошными кривыми – профили, соответствующие скорости ОПП V = -0.1 ct. Расчет профилей произведен для волнового числа, соответствующего линии 1 на рис. 3. Для волновых чисел, соответствующих линиям 2, 3 на спектре рис. 3, картина профилей аналогична. Отличие заключается в заметном увеличении амплитуд магнитного потенциала при возрастании волнового числа. Видно, что профиль высокочастотной моды, в отличие от профиля МСВ низкочастотной моды, сильно зависит от величины и знака скорости ОПП. Примечательно, что профиль магнитного поля в диэлектрическом зазоре практически не меняет своего вида при учете ОПП, а сильные изменения магнитного поля под влиянием ОПП происходят именно в движущемся кристалле.

Заключение

Проанализировано влияние ОПП на спектральные свойства щелевой МСВ в зазоре двух ферромагнитных пленок с продольной намагниченностью. Показано, что для высокочастотной и низкочастотной моды щелевой МСВ эффект Доплера из-за движения одного из кристаллов нормальный. Проведены численные оценки эффектов ОПП кристаллов, показывающие высокую «чувствительность» спектральных характеристик щелевых МСВ к движению одного из кристаллов щелевой структуры. Так, например, результирующий доплеровский сдвиг на два порядка больше, чем для электромагнитной волны той же самой частоты. Эту «чувствительность» магнитостатических волн к движению приемного устройства или самого активного кристалла целесообразно использовать в устройствах, сочетающих ОПП с обработкой сигнальной информации. Рассмотренные эффекты ОПП активных кристаллов могут быть полезны и при конструировании микромеханических устройств, датчиков скорости/ускорения и перемещения.