Макромеханическое моделирование упругой и вязкоупругой сред Коссера

Показано, что динамику континуума Коссера (микрополярная среда) можно моделировать движением двух стержней, упруго или вязкоупруго контактирующих между собой. Установлена связь между константами упругости среды Коссера и параметрами стержней, задаваемыми изначально. Впервые удалось ввести вязкоупругий оператор в модель микрополярной среды.

MACROMECHANICAL MODELLING

OF COSSERAT ELASTIC AND VISCO-ELASTIC MEDIA

V.I. Erofeev, V.V. Kazhaev and N.P. Semerikova

Nizhny Novgorod Branch of the Mechanical Engineering Research Institute RAS, Nizhny Novgorod, 603024, Russia

It is shown that the dynamics of a Cosserat continuum (a micropolar medium) can be modeled as a motion of two rods interacting elastically or visco-elastically. The relation between the elasticity constants of the Cosserat medium and the initial parameters of the rods has been established. For the first time a visco-elastic operator has been introduced in the model of a micro-polar medium.

В 2009 году исполняется 100 лет со времени опубликования работы Э. и Ф. Коссера [1]. Появление модели континуума Коссера ознаменовало собой начало перехода в теории сплошных сред от механики Ньютона, исходным объектом которой является материальная точка, к механике Эйлера, имеющей в качестве исходного объекта твердое тело. Именно как континуальное обобщение уравнений механики Эйлера модель среды Коссера интересует исследователей. Недостаточная на сегодняшний день практическая применимость модели Коссера обусловлена, главным образом, отсутствием двух факторов: методик надежного определения материальных констант и концепции учета вязкости такой среды.

В данной работе предпринимается попытка найти подсказку, как вводить вязкоупругие операторы в уравнение Коссера с помощью модели составного (слоистого) вязкоупругого стержня, идентичного по своим дисперсионным свойствам модели среды Коссера.

Деформированное состояние среды Коссера описывается несимметричным тензором деформаций γ _ji и тензором изгиба-кручения κ _ji [2]:

γ ji

∂u            ∂ψ

ⁱ -Ξ κ= ⁱ

∂ x_j^{j j} ∂ x_j

Здесь u_i — компоненты вектора перемещения; x j — декартовы координаты; ψ _i — компоненты вектора поворота, кинематически независимого от перемещений; Ξ _kji — псевдотензор Леви–Чивиты ( i = 1,2,3 ; j = 1,2,3; k = 1,2,3).

При рассмотрении адиабатических процессов упругого деформирования необходимо постулировать зависимость внутренней энергии U от инвариантов мер деформации (1).

Функция U раскладывается в окрестности естественного состояния ( γ _ji = 0, κ _ji = 0 ) в ряд Тейлора, величины второго порядка во внимание не принимаются. Для изотропного однородного и центрально-симметричного тела получается разложение следующего вида [2]:

µ+α µ-α λ γ+ε

U = ----Y-Y - ^--Y-Y-H—Y»Y ^--к к

2 γ ji γ ji      2 γ ji γ ij 2 γ kk γ nn     2 jiji

γ-ε β

+ 2 κ _ji κ _ij + 2 κ _kk κ _nn ,

где λ , µ — постояные Ламэ; α , β , γ , ε — новые упругие постоянные микрополярного материала, удовлетворяющие ограничениям [3]:

α≥0, γ+ε≥0, 3β+2γ≥0,  -(γ+ε) ≤γ-ε≤(γ+ε) .

В работе [4] найдена следующая зависимость между этими упругими постоянными:

µ(2γ+β)=(α+µ)(γ+ε) .

Объемная плотность кинетической энергии T состоит из двух слагаемых

T ₌ ρ∂ u_i ∂ u_{i +} I ∂ψ _i ∂ψ _i 2 ∂ t ∂ t 2 ∂ t ∂ t ^,

где ρ — плотность среды; І — константа, характеризующая инерционные свойства макрообъема, равная произведению момента инерции частицы вещества вокруг любой оси, проходящей через ее центр тяжести, на число частиц в единице объема.

Напряженное состояние определяется несимметричным тензором напряжений σ _ji и тензором моментных напряжений m_ji , вычисляемых через внутреннюю энергию (2):

∂ U σ= ; ji    _∂γ _ji

∂ U m ji ⁼

∂κ _ji

.

Уравнения динамики континуума Коссера имеют вид [2]:

д ² й

ρ

∂ t ²

- (X + 2ц) grad div й + (ц + a) rot rot й - 2a rot И = 0,

д 'v/

^ρ ∂ t ²

- (в + 2y) grad div И + (y + s) rot rot И - 2a rot й + 4a\p = 0.

Система (7) (см., например, работу [5]) позволяет описывать продольные упругие волны (волны дилатации), волны сдвига и волны вращения, подразделяющиеся на волны продольного (дилатационного) вращения и волны поперечного вращения. При этом сдвиговые волны и волны поперечного вращения связаны в линейном приближении.

Особенности распространения волн Рэлея вдоль границы микрополярного пространства рассмотрены в статьях [6, 7]. В работе [8] для модели континуума Коссера исследованы сдвиговые поверхностные волны, принципиально не описываемые уравнениями классической теории упругости.

Если вдоль оси x 1 = x распространяются плоская волна сдвига и волна вращения, то система (7) преобразуется к виду:

52 v /     х 52 v5у p—7 —(ц + a)—7 + 2a— = 0,

5t2 v      ’xx2

. 52w   z     x 5'u   ..5

I — ^--( y + e ) —-7 + 4 aw 2a— = 0.

512   v     ’ 5x2

Здесь v ( x , t ), v( x , t ) — компоненты векторов перемещения и поворота соответственно.

Система (8) сводится к одному уравнению относительно сдвиговых перемещений:

₂ d ² v _ ₂ ^ ^{5 2} v + I ^{5 4} v M ^{+ a}) I + p ( y + ^e ) 5 ⁴ v + (^ + a)(Y + s) d ⁴ v = 0

5 1 ² p 5 x ² 2 a 5 1⁴           2 ap 5 1 ²5 x ²        2 ap 5 x⁴

Волны, описываемые системой (8) или уравнением (9), обладают дисперсией. Закон дисперсии определяется решениями уравнения u + aY + E,4 f 4au 2^ + a Y + eTL 2 Ma a             zmx r---------k4 + —- —ro2 r----+ ----- k2 -го21--ro2 1 = 0.                  (10)

P I ( I P ( P I J J       k I J

Далее рассматривается составной стержень, представляющий собой совокупность двух стержней (слоев), находящихся в контакте друг с другом, причем сила контактного взаимодействия предполагается линейной вязкоупругой. Движение стержней, согласно [9], описывается системой уравнений:

E 1 S 1

5 ² u 1 5 x x

⁹ 2 ^и^Р(_и           u i ⁹ u 2 )

= Pi D i+ R ( U — U^ ) + R , ^{1 1} 5 1 ^{2       v 1     27     1} (5 1     5 1 J

„ _o 5² u _{2      o} 5² u _{2 n} / x _n f 5 u ₂ 5 u 1 )

E^S^ —7" = p₂ S^ —-—+ R ( u ₂ — u, ) + R, ---,

^{2 2} 5 x ^{2      2 2} 5 1 ^{2       v 2     17     1} ( 5 1     5 1 J

где u — продольные перемещения стержней; E_t , S i , p i ( i = 1,2) — их параметры (модули Юнга, площади поперечных сечений и плотности); R , R ₁ — коэффициенты упругого и вязкого взаимодействия стержней.

Вначале следует рассмотреть случай, когда сила контактного взаимодействия между стержнями является линейно упругой, то есть R 1 = 0. Тогда система (11) сводится к одному уравнению относительно перемещения отдельного стержня, например, u ₁ . Для этого достаточно выразить перемещение u ₂ из первого уравнения системы и подставить во второе. В результате получается уравнение вида:

(

1 +

к

p i 5 1 ^p u Р 2 5 2 ^р t ²

2   ^,2 ^p i ⁵ 1

к         p252 J

1 5 ² u + p i 5 1 ⁽ 5 ⁴ u 5 x ²    R

- ( C ? + C 2>14^ + c 2 C 2 f u 1= 0. (12) ^x ’ о t o x            о x )

Здесь C₁ = ^E₁ /p₁, C ₂ = ^E ₂ /p₂ — скорости продольных волн в стержнях, u = u₁ ( x , t ) .

Уравнение (12) по форме совпадает с уравнением динамики среды Коссера (9). Это дает возможность моделирования среды с микроструктурой посредством движения слоистого стержня. Сопоставление коэффициентов уравнений (12) и (9) приводит к системе уравнений, позволяющей выразить упругие константы микрополярной среды через параметры стержней:

1 . ^{p 5} = 2; C 2 + C ₁ ^{2 p 5} = 2 ^H ;

^p 2 ⁵ 2                     ^p 2 ⁵ 2      ^p

pi5i /C2 + C2 4 = (ц + а)I + (y + s)p .R ( 12)       2ap ;

p i 5 i = I .

R   2 a ;

,2Г2 pi51   (H + a)(y + s)

C T =

¹² R 2 ap

Соотношения (13) могут быть представлены в виде:

ц С2 + С2   y + 8 „2 а С2 - С2    Ip,

12          1211

,                      С^ ,, p 2 I 2 p 2      2a

Из (4) находится еще одно соотношение:

P + 2y = 2 C² C ₂ ²

i  " C 1 + c 2"

Как видно из выражений (14), (15), скорость сдвиговой волны C _т =

ц

и скорости

N p

волн вращения C _v =

у + 8

I

г _ в + 2у , C в        i

в среде с микроструктурой зависят только от

скоростей продольных волн в стержнях. Для разных композитных материалов соотношения между характерными скоростями упругих волн могут быть различными. В частности, в работе [10] показано, что для композита «алюминиевая дробь в эпоксидной матрице» характерные скорости распределяются следующим образом: C _в >  C ^ >  C _т .

Поскольку параметры стержней задаются заранее, то для соответствия среде Коссера необходимо, чтобы их плотности и площади поперечных сечений были пропорциональны

(p,

— = — , а модули Юнга подобраны так, чтобы выполнялось kp2

EE условие — >  —¹ .

р2

Для введения трения в модель среды Коссера считается, что сила контактного взаимодействия между стержнями является линейной вязкоупругой (R1 ^ 0) и движение стержней описывается системой уравнений (11). Как и в предыдущем случае, эта система сводится к одному уравнению. Так сложение обоих уравнений системы (11) дает связь б 2 Uj вида Р151^тт б t

E ₅ ^62И 1 = E ₅ ^{б 2 и} 2

¹¹ б x^{2      2 21} б x²

^{б и} 21

р₂ 5 1 — 2г . Из первого уравнения также следует, ^{2 21} б t ²

б и₂ б ² и что Ru + R —² = р, 5 , —,1

^{2 1} б t ¹¹ б t ² полученных соотношений относительно и = и 1 ( x , t ) ,

б 2 И        , и И

• - EA — + Ru , + R  ¹ . В результате подстановки

• ¹¹ б x ^{2       1    1} б t

во второе уравнение системы находится уравнение отличающееся от уравнения (12) только наличием диссипативных слагаемых:

б ² и C ² + C ² б ² и р, 5 (б ⁴ и               б ⁴ и

, 2 б 4 и ] ² б x ⁴ ,

¹ +    ^- C 2 + С ₂2

б t ²        2     б x ²     2 R ( бt^{4 V 1      2!} б t² б x ²

R 1 ( б ³ и _- C 1² + C ₂ ² б ³ и ' R ( б t ³       2 б t б x ² ,

Все остальные слагаемые остаются без изменения, поэтому выражение (16) можно

R интерпретировать как уравнение среды Коссера с внутренним трением. Здесь 1 —

R коэффициент диссипации, а упругие константы микрополярной среды связаны с параметрами стержней соотношениями (13), (14). Таким образом, в микрополярную среду удается ввести вязкоупругий оператор. В модели Коссера диссипация определяется слагаемыми, пропорциональными uttt и utxx , что напоминает модель внутреннего трения по Максвеллу [11].

Для анализа дисперсионных и диссипативных свойств волн в уравнении (16)

_ _ _   _      _                    _                  с2 + C72 t x , и осуществляется переход к безразмерным переменным: t = —1----- —, x = —, и = —,

2 rru ₀

/ с ² + с ₂² pj 5                    .

где и₀ — характерная амплитуда волны, r =, —¹---²—— — некоторый

0                                                      2R пространственный масштаб. В результате уравнение (16) принимает вид (штрихи над безразмерными переменными опущены):

б ² и   б ² и     б ⁴ и d б ⁴ и 1 б ⁴ и   ,( б ³ и     б ³ и

бt2   бx2   б12бx2 + бx4 + 2 бt4 + ^бt3   бtбx2 v

В выражение (17) входят два безразмерных параметра, один из них

—

2C2C2                                              R d =----1—^^-, определяет дисперсию, а второй — о= , 1 , — диссипацию. Для

(C22 + C12)                                                   VP151R дисперсионного параметра можно легко получить оценку, если воспользоваться неравенством Коши между средним арифметическим и средним геометрическим (a + b > 24ab, (a, b > 0, a ^ b)). Очевидно, что параметр дисперсии удовлетворяет 1

неравенству d <  2, а наличие диссипации приводит к тому, что частота и волновое число линейной волны связываются комплексным дисперсионным соотношением:

to2 - к2 + to2к2 - dk4 -1 to4 + i5rn3 - i5tok2 = 0.

Уравнение (18) является биквадратным относительно волнового числа k ; из его решения получается зависимость вида k1,2

2 d

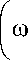
-1 - i5w ± ^(w2 -1 - i5w) - 2dw4 + 4id5w3 + 4dw2 j

Из формулы (19) видно, что волновое число является комплексным k = к " + ik ", где к' = Re( к ), к" = Im( к ). Это означает, что волна имеет постоянную распространения к' и затухает по экспоненциальному закону с коэффициентом затухания к ".

На дисперсионной плоскости (w, к"), где к' — действительная часть комплексного волнового числа k , существуют две дисперсионные ветви, выходящие из начала координат. При этом одна ветвь в низкочастотном диапазоне приближается к прямой w = к', а в высокочастотном выходит на асимптоту w = к'V1 - V1- 2d . Вторая ветвь 2d выходит из начала координат по прямой w =----к , угол наклона которой уменьшается 5

с ростом коэффициента диссипации 5 . В высокочастотном диапазоне эта ветвь приближается к асимптоте w = к 'V1 - V1 - 2 d , не зависящей от 5.

Качественный вид дисперсионных зависимостей w ( к ' ) приведен на рисунке (часть а ). Здесь и на последующих частях рисунка кривые получены при значениях безразмерных параметров d = 0,25; 5 = 0,1.

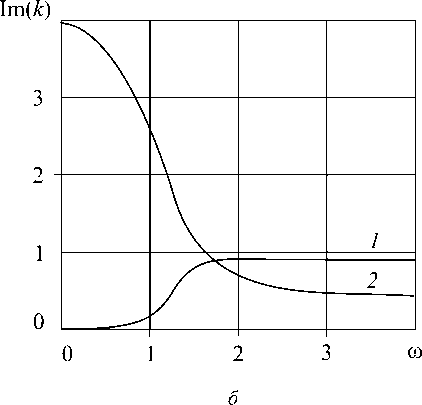
На части б представлены зависимости мнимых частей к" волнового числа к от частоты w . На плоскости ( к ", w ) также имеются две ветви, одна из которых (кривая 1 ) выходит из начала координат и с увеличением частоты приближается к горизонтальной 5 ( 1 - Р ² )                      1

асимптоте к" =---)---, _ч, где p = ,       =. Вторая ветвь (кривая 2 ) к " выходит

2 Р (2 dp1-1)         V1 + VT-2d из точки w = 0, к" = Д= и убывает с ростом частоты, приближаясь к горизонтальной V 5

асимптоте

к =

5(1 - Р2)

, где

2 р 1 ( 2 dp 1² - 1 )

р 1 = ■      =. Таким образом, в низкочастотном

V1 - V 1 - 2 d

диапазоне коэффициент затухания к зависит от частоты волны, а в высокочастотном диапазоне затухание становится частотно-независимым, так как при этом усиливается влияние дисперсионных эффектов.

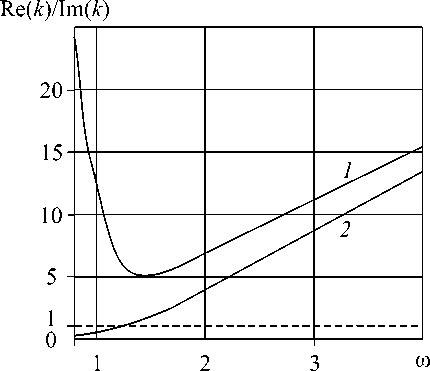
Часть в содержит частотные зависимости отношения Re ( к )/Im ( к ) . Неравенству

[ Re ( к )/ Im ( к ) ] >  1 соответствуют области частот, где процесс распространения волны преобладает над процессом ее затухания.

В частном случае, при 5 = 0 (упругая среда), из выражения (19) получается решение дисперсионного уравнения континуума Коссера (10):

22 к ₂ = I w ² - 1 ±J ( 1 - 2 d ) (1 -w ²) + 2 d I .

^1,2 V2 d I                   ^v              J

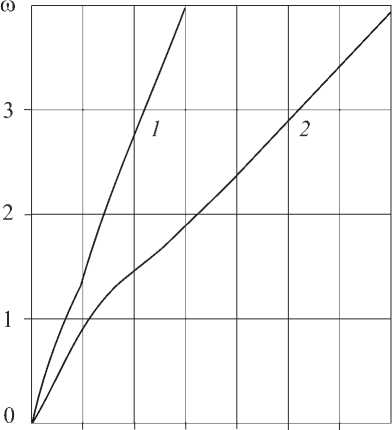
В этом случае на дисперсионной плоскости (ю, к) существуют две дисперсионные ветви (кривые 1, 2). Исходная точка первой ветви совпадает с началом координат и имеет асимптоту ю = к в низкочастотном диапазоне, а при больших частотах выходит на асимптоту ю = 41 - V1 - 2 dк (часть г). Вторая дисперсионная ветвь появляется при частотах ю > V2 , что соответствует в размерных переменных значению ю > 2^^. В высокочастотном диапазоне асимптотическое решение имеет вид: ю = 1+ + V1- 2dк.

0   1   2   3   4   5   6 Re№

а

в

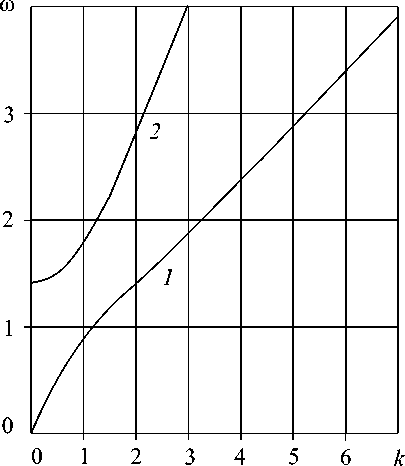
Рис. Дисперсионные характеристики среды Коссера: а , б , в – среда вязкоупругая; г – среда упругая

Сравнение дисперсионных зависимостей в обоих случаях показывает, что диссипация оказывает влияние на дисперсионные свойства волн только в низкочастотном диапазоне. В высокочастотном диапазоне диссипация не проявляется, так как дисперсионные ветви при δ = 0 и при δ ≠ 0 выходят на одинаковые асимптоты.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 09-08-00827).