Макроскопическая космология ранней вселенной

• 1.    Гравитационные возмущения изотропной Вселенной

  • 1.1.    Общие соотношения

Метрику с поперечными гравитационными возмущениями запишем в виде (см., например, [1]):

ds0 = a2(n)(dn2 — dx2 — dy2 — dz2);(1.1)

ds2 = ds0 + a2 (п)һав dx5 dxe ；(1.2)

hae = eae S (n)einr,(1-3)

rje S(n) — амплитуда гра.вігтатіііоішых воли. Далее： ha = һүв goY 三 - a2 hae ； h ≡ hαα ≡ g0αβ hαβ ≡

--2 ^(h11 + ^h22 + ^h33 )，                                          ( L5 ) a²

причем для гравитационных волн h^na = 0；(1-G)

h = 0.

Вследствие (1.7) в линейном по h приближении:

V-Š 仁 V-ŠČ = a4.

Будем решать уравнения Эйнштейна с космологическим членом2:

Gik - 人 gik = ⁰ ，                                             ( .1-9)

rje Gik = Rik - 1/2Rgik — т ( ?ігзор Эіпішт ( ?ппа. Будем разлагать в ряд т ( ?ігзор Эйіішт ( ?ппа по малости амплитуды гравитационных воли S(n )・ При этом, пользуясь изотропией ііевозмущеішой метрики, удобно ввести локальную систему координат, в которой:

n = n(0, 0,1); s = (1,0, 0),

(1-Ю)

rje s - едііішчпып вектор полярігзатцііі поперечных возмушеішп. В зтоіі системе координат hi2 = 0; hii = -h22 = S(n)einz,                               (1-11)

В произвольной декартовой системе координат трехмерного евклидова пространства E3 тензор поляризации e 〃 k формулы (1.5) имеет вид:

nαnβ

(1-12)

(1-13)

^еав — 2sase 十 n2 Оав, s ² = 1; sn = 0, n ² = n ² .

Легко проверить, что при этом автоматически выполняется калибровочное условие (1.6).

Запишем уравнения Эйнштейна с космологическим членом во втором приближении по гравитационном возмущениям:

Gi? + Gi? + Gi2 ) = 人 a*                              (1-14)

и усредним эти уравнения по всем направлениям волнового вектора n3

(1.15)

һав = 0.

Таким образом, мы получим макроскопические уравнения Эйнштейна во втором порядке по возмущениям гравитационного поля:

Gi^{0 )} = -礎 + 人 9 化                          (1-16)

согласно которым поправки второго порядка можно рассматривать как тензор энергии-импульса гравитационных возмущений:

Tik =- 厶 Gf.                             ( L17)

Заметим, что на фоне изотропного пространства Фридмана операция усреднения по направлениям сводится к вычислению интеграла по двумерной сфере радиуса n:

丽 ^r ) = 4п /

ф( п , r )dQn.

(1.18)

Разлагая тензор Эйнштейна по возмущениям вестные выражения:	метрики, в нулевом приближении получим из-
(0 )         ( 0 )         ( 0 ) 一 G11 = G22 = G33 一	с a" а'2                                                  .. =2 —- 縞 ;                       (L19) a ' 2 G44 = 3 —2.                                  (、 1-20)

Таким образом, в нулевом по гравитационным возмущениям приближении мы получили бы стандартное уравнение Эйнштейна с А - членом

а" /= 1А                                     (1-2D 3 и его инфляционное решение:

(1-22)

a =-- η

/.2. Уравнение для амплитуды гравитационных волн

В линейном по S приближении получим единственные нетривиальные компоненты:

G11) = У ： 〉 三 SG = jeinz S 〃 + 2 JS ， + S ( n² + 2 《 - 4.            (1.23)

Ковариаіітио обобщая результат в E3, запишем:

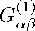
(Ьав - ^2sase)^SG.

(1-24)

Подставляя выражение (1.23) в уравнения Эйнштейна (1.9), получим уравнение для амплитуды поперечных возмущений:

S" + 2 £ S' + $ (n² + 2 О² — 4 g + 人 a) = 0.

Это уравнение с учетом соотношений (1.19) можно записать в более простом виде:

S 〃 + ² S' + (n² - 2G11) + Aa2)S = 0.

(1.25)

(1-26)

В частности, при подстановке сюда инфляционного решения нулевого приближения уравнений Эйнштейна (1.22) уравнение (1.26) сводится к следующему:

S'' - 2 — + S

(n^{2 -}亲)

0,

(1.27)

которое имеет своим решением:

S = Cin3/2J“(nn) + Cin3/2Y“(nn),                              (i.28)

(1-29)

〃 =— ， 3 + 4 /<・

В частности, вблизи космологической сингулярности нулевого приближения п т —а, стало быть, ii |nn| т а уравнение (1-2G) сводится к уравненшо ：

S'' + n2S = 0,

(1.30)

(1-31)

имеющему своим решением обычные ВКБ-решения:

S = Cieinn + C2e-inn, которые, кстати, можно получить и из точного решения (1.28) в этом пределе.

/.3. Второе приближение

Вычисляя тензор Эйнштейна второг приближения, получим его нетривиальные компоненты:

G11) = G22) = e2inz (4 S 2n2 + SS'' + 4 S '2 + 2 £ SS'}                    (1.32)

G33) = e2inz (4 S2n2 + SS'' + 4 S'2 + 2 J SS'}                    (1.33)

G44) = —e2inz (4S2n2 + 4S'2 + 2 JSS') .                   (1.34)

Ковариаіітио обобщая результат в E3, запишем:

GJ =e^2inr(USae- V*) ，                       (L35)

где

'

U = 4 S2n2 + SS'' + 4 S'2 + 2 --SS';                            (1.3G)

V = S2n2 — 2 S '2.                             (1.37)

Усредняя (1.35) по направлениям распространения возмущений с учетом очевидного равенства na ne — Т^Ьавn ,                                        (1-38)

получим для усредненных компонент G ； *' следующее выражение:

G(k) = 8n(E + P)UiUk - 8nPgik,

(1.39)

где¹ ui - времениподобный вектор скорости наблтодателя. a E ii P - плотность энергии п давление поперечных гравитационных возмущений:

P

E=1 (7 S ²n²+4 S”^{- 2} a SS ， ) 白( 12 S²n²+12 S ， ²⁺²SS ，营 +

(1-40)

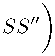
(1-41)

В частности, для ВКБ-решения (1.31) эти формулы приводят к эффективному ультрареляти-вистскому уравнению состояния:

E ^ 鳥 2 S²n^{2 ；} P- 鳥 S²n²=3 E.

(1-42)

(1-43)

2.    Макроскопические уравнения Эйнштейна второго порядка по гравитационным возмущениям для Вселенной Фридмана

Объединяя полученные результаты в рамках уравнений (1.14) и (1.16), получим самосогласованную систему обыкновенных дифференциальных уравнений второго порядка, описывающих космологическую эволюцию пространственно плоской макроскопической Вселенной с учетом поперечных гравитационных возмущений:

S" + 2 JS ， + S (n² + 2О² - 4 a + 人 a²) = 0;

(2.1)

(2.2)