Максимальные коммутативные инволютивные алгебры в гильбертовом пространстве

можно рассматривать векторное пространство всех бесконечномерных п х п-матриц над полем комплексных чисел и изучать проблему описания всех подпространств этого векторного пространства, являющихся инволютивными алгебрами.

Существует много различных классов операторных алгебр в гильбертовом пространстве, включая классы ассоциативных алгебр неограниченных операторов в гильбертовом пространстве. Большинство инволютивных алгебр неограниченных операторов, например ]-алгебры, EC ^]-алгебры и EW ^]-алгебры [4], инволютивные алгебры измеримых операторов, присоединенных к конечной (или полуконечной) алгебре фон Неймана [5], мы можем представить как алгебры бесконечномерных матриц. Если мы сможем описать все максимальные инволютивные алгебры бесконечномерных матриц, то ряд проблем операторных алгебр, включая инволютивные алгебры неограниченных операторов можно свести к проблемам максимальных инволютивных алгебр бесконечномерных матриц. В частности, ряд проблем коммутативных операторных алгебр, включая коммутативные инволютивные алгебры неограниченных операторов можно свести к проблемам максимальных коммутативных инволютивных алгебр бесконечномерных матриц. В данной работе обсуждается проблема описания всех максимальных коммутативных инволютивных алгебр бесконечномерных матриц.

Всюду в данной работе п — произвольное бесконечное кардинальное число, S — множество индексов мощности п. Далее, пусть {eij } — семейство матричных единиц такое, что eij — п х п-мерная матрица, eij = (а^ав)_аве=, (i,j )-ая компонента которой равна 1, а остальные компоненты равны нулю.

Пусть {m^} — семейство п х п-мерных матриц и m^ = (m^)авег для каждого индекса ф Тогда через ^2^ m^ обозначим матрицу, компоненты которой являются суммой соответствующих компонент матриц из семейства {m^ }, т. е.

_{ξ            ξ}        α,β ∈ Ξ

Здесь подразумевается, в сумме P^ m^ число ненулевых членов не более, чем счетно.

Обозначим через Mn(C) множество п х n-мерпых матриц (Ai’j )i,jes такое, что для каждой пары индексов i, j из S, Ai’j G C, и существует такое неотрицательное число K G R, что для всех п G N и {eikу }ni₌i С {eij } имеет место

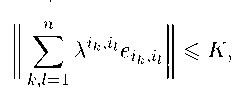
n

6K где II zLn i=i Aik ’il eik i || является норм ой матрицы Pn i=1 Aik ’il eik у в конечномерной С*-алгебре, порожденной системой матриц {eikу}П1=Г Легко видеть, что относительно сложения матриц и умножения матрицы на число множество Mn (C) является векторным пространством над полем комплексных чисел C.

В векторном пространстве

Mn = {(Ai’j)i’Щ5 : Ai’j G C (Vi,j G S)} всех п х п-мерных матриц над полем комплексных чисел C введем ассоциативное умножение следующим образом: для произвольных элементов x = (Ai’j )ijes, y = (p j )i js n'3 Mn определим произвсдепие x ii y как xy = ( 52 Ai ’5 / ’j

Очевидно, что относительно этой операции векторное пространство Mn не является алгеброй. В то же время, его подпространство Mn(C) становится ассоциативной алгеброй и Mn(C) = B (12(H)), г де 12(H) — комплексное гильбертово пространство квадратично суммируемых семейств {xi}_ie=, B(12(H)) — алгебра всех ограниченных линейных операторов в гильбертовом пространстве 12(H). Поэтому Mn(C) является алгеброй фон Неймана всех (бесконечномерных) n х n-мериых матрии над C [2].

Напомним, что гильбертово пространство H — это бесконечномерное евклидово пространство, являющееся полным метрическим пространством относительно метрики порожденной скалярным произведением данного евклидова пространства [3, §1.5].

Пусть A (Mn) — множество всех векторных подпространств векторного пространства, Mn. являющихся коммутативными инволютивными алгебрами и 6 — порядок в A(M_n ), определенный следующим образом: для произвольных коммутативных инволютивных алгебр X. Y iгз A(Mn ) пишем X 6 Y. если X является подмножеством Y. т. е. X С Y. Этот порядок в A (Mn) удовлетворяет условиям леммы Цорна. Поэтому, для каждого элемента A G A (Mn) существует максимальный относительно этого порядка элемент A G A (Mn) тако!i. что A 6 A.

Определение. Максимальный относительно порядка 6 элем епт A множества A(Mn ) будем называть максимальной коммутативной инволютивной алгеброй в гильбертовом пространстве 12(H).

Пусть {ei }ie= — максимальное ортогональное семейство минимальных проекторов алгебры B(12(H)) и {eij}гуег — система матричных единиц построенная по семейству {ei}ie=. Далее. пусть a — пропзвольпый элемент из Mn. Мы будем писать a = Е Aij eij, если ei,iaej,j = Аг<)eij для каждой пары i, j различных индексов из H.

Теорема 1. Множество всех ограниченных элементов максимальной коммутативной инволютивной алгебры в гильбертовом пространстве 12(H) является алгеброй фон Неймана.

C Пусть A — максимальная коммутативная инволютивная алгебра в гильбертовом пространстве 12(H) 11 Ab — подалгебра, всех ограшнгенных элементов алгебры A. Тогда существует максимальная коммутативная инволютивная подалгебра Ao алгебры B(12(H)), содержания алгебру Ab. Берем произ вольную сеть (а_а) элемеитов A. утьтраслабо сходящуюся к элементу a из B(1₂(H)). Тогда ■ элемент a .тежнт в Ao.

Предположим, что Ao содержит максимальное ортогональное семейство {e_i,i}_ie= минимальных проекторов алгебры B(12 (H)). Тогда спектральное разложение элемента a имеет следующий вид:

a = X Ai’ie^, i∈Ξ т. е. a является ультраслабым пределом сети {Aiieiylies. Пусть для каждого a aα

= E3"e_w. i ∈ Ξ

Так как сеть (aa) утьтраслабо сходнтся к элементу a в B(12(H)). то для каждого i сеть {Aai}ie= сходится к Ai’i. Берем произвоявный элемент b из A. 1Бгеем aab = baa для каждого а. Докажем, что ab = ba. Пусть b = £ Aij e.u, где {eij}i,jes — система, матричных едишin построенная по семейству {e,}ie=. Имеем a„b = (£ Л«еД ( £ Aijej = £ A“Aijey i∈Ξ             i,j∈Ξ               i,j∈Ξ b = £ Aij A" e,,.

Следовательно, для каждой пары i, j индексов из 5 имеем

A^Ai-j = Aij A" .

Так как комплексное число A,,, является пределом сети ДДД, то отсюда получаем, что для каждой пары i. j индексов из 5 имеем

Ai’iAij = Aij Ajj.

Следовательно, ab =

A^e,,i\ ( 52 Aij e,,j) = 52 Ai’iAije,j = 52 A^j Ajj e,,₃ = ba. i ∈ Ξ             i,j ∈ Ξ               i,j ∈ Ξ                 i,j ∈ Ξ

Поэтому элемент a лежнт в A. a 3iгатит а лежит и в Ab. Следов;ттелыю. Аь является ультраслабо замкнутой, т. е. является алгеброй фон Неймана.

Теперь рассмотрим общий случай. Спектральное разложение элемента a имеет следующий вид: существует единственное ограниченное разложение единицы Ah e^ (A G R) во множестве всех проекторов алгебры Ao такое, что kak

/

λ deaλ .

-kak

При этом для элемента x G B(12(5)) будет a о x в том и только в том случае, если x о е^ для всех A G R. Пусть для каждого а kaαk aα

λ deλα .

-kaαk

Берем ортогональное семейство {ев,в} проекторов из Ao такое, что всякий проектор из семейства {e^} U (U_a{ea}) представляется как точная верхняя грань некоторого подсемейства семейства {ев,в}• Далее рассуждаем также как и ранее, в

Пусть {e, },е= — максимальное ортогональное семейство минимальных проекторов алгебры B(12(5)). Нерез P^L= e,C обозначим миожеотво всех элементов a iiз Mn таких, что eiaej = 0 для каж,той пары i. j различных индексов из 5. Тогда miюжество P^L= e,C является инволютивной алгеброй относительно введенной выше операции умножения и имеет место следующая теорема.

Теорема 2. Алгебра P®L₅ eiC является максимальной коммутативной инволютивной алгеброй в гильбертовом пространстве 12 (H).

C Пусть b — произвольиый элемент из Mn такоз1. что ab = ba для каждого элемента a 113 Pi® = ei C Тогда eib = bei (V i E H).

Отсюда eibej = beiej = 0 для каж,той пары i. j различных индексов из H. Поэтому элемент b лежнт в P^= eiC. Ввиду произволыюстп элемента b алгебра, Pi_r- eiC является максимальной коммутативной инволютивной алгеброй в гильбертовом пространстве ¹2^(H) B

Пусть Ao — максимальная коммутативная инволютивная подалгебра алгебры B(1₂(H)). P a _o — множество всех njзоекторов из алгебры Ao. Нерез P a _o (C) обозначим множество всех элементов а из Mn таких, что eaf = 0 для каждой пары e, f ортогональных проекторов из P a _o. Тогда множество P a _o (C) является векторным пространством и имеет место следующая теорема.

Теорема 3. P a _o (C) является максимальной коммутативной инволютивной алгеброй в гильбертовом пространстве 12(H).

C Сперва, дозсажем. что Pao(C) является алгеброй. Пусть a. b — произвольные элементы из Pao (C) 1i e. f — произвольная пара, орте мочальных проекторов из Pao. Тогда по определению eaf = fae = 0, ebf = fba = 0.

А также 1 — e — f E Pao и по определешпо ea(1 — e — f) = 0. Отсюда eabf = ea(e + f + (1 — e — f ))bf = eaebf + eafbf + ea(1 — e — f )bf = ea0 + 0bf + 0bf = 0.

Следовательно, произведение ab лежпт в P a _o (C). Можно проверить непосредственно, что остальные аксиомы инволютивной алгебры также имеют место для P a _o (C).

Теперь докажем, что инволютивная алгебра Pao(C) максимальна в гильбертовом пространстве 12(H). Пусть b — произволыилй элемент из Mn такой. что ab = ba для каждого элемента a iiз Pao (C). Тогда eb = be (V e E PAo (C)).

Отсюда ebf = bef = 0 для каж,той пары e. f различных проекторов из P a _o. Поэтому элемент b лежнт в P^o. Ввиду произволыюстп элемента b алгебра, Pa_o является максимальной коммутативной инволютивной алгеброй в гильбертовом пространстве 12(H). B

Теорема 4. Пусть {ei}_ie= — максимальное ортогональное семейство минимальных проекторов алгебры B (12(H)) и A — максимальная коммутативная инволютивная алгебра в гильбертовом пространстве 12(H), содержащая элемент a такой, что eiaei = Ai, ejaej = Aj, Ai = Aj и eiaej = 0 для каж/т,ой пары i, j различных индексов из H. Тогда A = Pi® = eiC.

C Берем произвольный элемент b iiз A. Изюсм ab = ba. Пусть b = XX xj eij, где {eij}i,jes — система матричных единиц построенная по семейству {ei}ie=. Тогда a = X Ai,iei,i, i∈Ξ что означает eiaej = 0 • eij для каждой пары i, j различных индексов из 5. Имеем ab = (X Ai’ieE ( X X^jj = X ^ Aj«^ i∈Ξ             i,j∈Ξ               i,j∈Ξ

И ba =       A^i,jA^j,j e i,j .

i,j ∈ Ξ

Следовательно, для каждой пары i, j индексов из 5 имеем

Ai’iAi’j = Ai-j Ajj.

Так как Ai’i = A jj то A^i,j = 0 для каждой пары i, j различных индексов из 5. Следовательно. ei be j = 0 для каж,той пары i. j различных индексов из 5. т. е. b Е P ^L= eiC Что и требовалось доказать, в

ЗАМЕЧАНИЕ 1. В силу теорем 1, 2 и 3 множество максимальных коммутативных инволютивных подалгебр алгебры B(12(5)) инъективно вкладывается во множество A ( M n ). Действительно, пусть M (B(12(5))) — множество всех максимальных коммутативных инволютивных подалгебр алгебры B(1₂(S)). Рассмотрим отображение ф : M (B(l₂(S))) ^ A ( M n) определенное как

ф(AO) = A, Ao Е M(B(12(5))), A Е A(Mn), если AO C A. В силу теорем 2. 3 для каждой алгебры Ao Е M(B(12(5))) сутпеетвует единственная алгебра, A Е A(Mn) содерткащая Ao. Поэтому о1тображетше ф является инъективным, и вообще мы предполагаем, что ф является биективным отображением, т. е. для каждой алгебры A Е A(Mn) сутпеетвует едшкзтвеппая алгебра, Ao Е M(B(12(S))). содержащаяся в A. Вопрос о том, верно это или нет, остается открытым.