Масштабно-зависимая модель электроупругости для сплошного цилиндра с покрытием

Пьезоэлектрические элементы цилиндрической формы широко используются в качестве сенсоров и актуаторов в микро-электромеханических устройствах [1]. В таких структурах в связи с тем, что размеры исследуемых элементов могут быть соизмеримы с характерными размерами микроструктуры материала, согласно экспериментальным данным наблюдаются масштабные эффекты [2, 3], т. е. зависимость напряженно-деформированного состояния (НДС) от характерных размерных параметров.

• ^# Исследование выполнено за счет гранта Российского научного фонда № 22-11-00265, https://rscf.ru/ project/22-11-00265/.

• (0 2023 Ватульян А. О., Нестеров С. А.

Задачи деформирования и колебаний пьезоэлектрических тел цилиндрической формы достаточно полно изучены в рамках классической теории электроупругости [4–6]. Так, в [5] отражены общие вопросы деформирования и колебаний пьезокерамических цилиндров с постоянными характеристиками, представлено большое количество постановок задач.

Однако классической теории становится недостаточно для моделирования масштабных эффектов. В настоящее время для учета масштабных эффектов применяется неклассическая механика, основанная на градиентных моделях, которая в определяющие соотношения включает градиентные параметры размерности длины [7]. По своему физическому смыслу масштабные параметры определяют протяженность неклассических масштабных эффектов. Значения масштабных параметров для монокристаллов имеют порядки межатомных расстояний (микроны). Однако для композитов масштабные параметры могут значительно превосходить параметры межатомных расстояний и определяться размерами ячейки периодичности материала. К основным методам определения масштабных параметров относятся: 1) испытание микроразмерных балок на изгиб; 2) сопоставление соотношений континуальной градиентной теории с оценками, получаемыми на основе молекулярной динамики; 3) испытание образцов с различным размером дефектов.

Градиентная теория упругости (ГТУ) получила свое развитие в середине XX века в работах Тупина [8] и Миндлина [9] и в дальнейшем получила обобщение на механику связанных полей, в том числе на теорию термоупругости [10] и электроупругости [11].

Современные исследования в области градиентной электроупругости можно разделить на две группы: одна в рамках теории градиентной упругости учитывает влияние градиента деформации, но не учитывает градиент электрического поля [12], другая учитывает влияние градиента электрического поля, но пренебрегает эффектом градиента деформации [13]. Градиентные модели электроупругости приводят к увеличению порядка дифференциального оператора в уравнениях равновесия или электростатики, причем старшие производные входят в соответствующие дифференциальные уравнения с малыми параметрами.

Впервые задача Ламе в рамках ГТУ для однородного цилиндра была поставлена в [14]. В случае однородного цилиндра в [15, 16] были получены точные аналитические решения ГТУ. Аналитические решения получены также и в случае упругого неоднородного полого цилиндра со степенным законом изменения коэффициентов Ламе [17].

Градиентная механика широко применяется также и для исследования поведения физических полей в окрестности поверхностей сопряжения и трещин. Некоторые задачи градиентной механики для слоистых тел (балки, полосы, цилиндра) рассмотрены в [18– 21].

В [22–24] представлено численное решение задачи градиентной электроупругости для полого функционально-градиентного цилиндра со степенными законами неоднородности. Однако задача градиентной электроупругости для сплошного цилиндра с покрытием остается неизученной.

Целями данной работы являются: постановка задачи градиентной электроупругости для сплошного цилиндра с покрытием; получение точных аналитических решений в случае однородного покрытия и численных решений на основе метода пристрелки в случае неоднородного покрытия; вычисление радиальных смещений и напряжений двухслойного цилиндра; сравнительный анализ полученных результатов.

• 2.    Определяющие соотношения градиентной электроупргости

Пусть пьезоэлектрическое тело занимает объем V с поверхностью S — S u U S p — S φ ∪ S _q . Ограничиваясь только влиянием градиента деформации, т. е. не учитывая влияние градиента напряженности электрического поля, плотность электрической энтальпии можно представить в виде [12]:

g ( ^E ij , ^E ij,k , E i )

— 2 c ijkl ^E ij ^E kl    e kij ^E ij E k   2 ⁶ ij ^E i ^E j ⁺ 2 A ijklmn ^E ij,k ^E lm,n ,

где E i — — ф ,i — компоненты вектора напряженности электрического поля, ф - электрический потенциал, E ij — 1 ( u i,j + U j,i ) — компоненты тензора деформации, u i — компоненты вектора перемещения, c ijkl и A ij kl_mn — компоненты тензоров модулей упругости 4-го и 6-го порядка, e _kij — компоненты тензора пьезомодулей 3-го порядка, ǫ ij — компоненты тензоров коэффициентов диэлектрической проницаемости 2-го порядка соответственно.

Математическая постановка задачи градиентной электроупругости, полученная путем применения вариационного принципа, имеет вид [12, 25]:

aij,j — 0,                                                (2)

m ijk,k n j n k — s i ,   T ij n j

-

Di i — 0 , ,

^m ijk,k ⁿ j

-

U i — V i ,   u i,i n — — ,

D j n j — q, ф — V o .

^{( m} ijk,k n k Xj ^{+ ( m} ijk,k n j n k ) ,s n s — pi , ∂v i

Здесь a j — T ij — m ijk,k — компоненты тензора полных напряжений, T ij — д^

C ijkl E ki — e kij E k — компоненты тензора напряжений Коши, m ijk — Е- — A ijkimn E im,n ij,k

компоненты тензора моментных напряжений, D i — — "E — e j E jk + E ij E j — компоненты вектора электрической индукции, p i , s i — компоненты векторов заданных сил на поверх-

ности тела, q — плотность поверхностного заряда, n i — компоненты единичного вектора нормали к поверхности тела в рассматриваемой точке.

Выпишем в полярной системе координат выражения для ненулевых компонент тензоров полных напряжений а фф — Т фф — ^{1 —} ( гт ффг ) — ¹ ( т фгф + т ^фф ) , а _ТТ — т _тт — rdb ( rm- r-r-r ) + ¹ ( т фгф + т _тфф ) , напряжений Коши т _ТТ — С 33du r + С 13 u r + е зз -^ , Т фф — c i3 du r + С 11 u r + е з1 ^ , моментных напряжений т _тфф — т ф_тф — 2 l ² (^Trr-Е ) , m _rrr — l ² d-r r , т ффг — l ² dsr ^ , вектора электрической индукции D _T — — 6 33 -^ + е з1 U r + е зз d- r и поверхностной нагрузки p _r — Т _тт — ¹ -d ( rm _TTT ) + 1Г ( т фф_г + т ф_гф + т _гфф ) . Здесь l — механический градиентный параметр.

• 3.    Постановка задачи для сплошного цилиндра

В рамках градиентной модели (2)–(6) рассмотрим задачу о деформировании бесконечного сплошного кругового неоднородного пьезокерамического цилиндра радиуса a с радиальной поляризацией. Электроды на поверхности цилиндра отсутствуют. К боковой поверхности цилиндра r — а приложена постоянная нормальная механическая нагрузка p . Математическая постановка задачи имеет вид:

dσ

rr

dr

+

σ rr - σ φφ r

— 0 ,

dD r + D r = 0 dr r

D r ( a ) = 0 , m _rrr ( a ) = 0 ,    p _r ( a ) = p o .

Здесь σ _rr и σ φφ — радиальная и окружная компоненты тензора полных напряжений, D _r — радиальная компонента вектора электрической индукции, m _rrr — радиальная компонента тензора моментных напряжений.

После интегрирования уравнения электростатики (8) с учетом граничного условия (9) и исключения электрического потенциала из соотношений для радиальной и окружной компонент напряжений Коши согласно [6] получим следующие модифицированные выражения для напряжений Коши:

_{∗     ∗} du _{r      ∗} u _{r      ∗      ∗} du _{r ∗} u _r

Trr = c3377 + c137’ тфф = c1377 + c117, где c^ = C11 + ^, c13 = C13 +     , c33 = C33 + ^ •

После исключения электрического потенциала задача электроупругости (7)–(10) сво- дится к задаче градиентной теории упругости с ужесточенными модулями упругости.

Введем безразмерные параметры и функции по формулам: € = a , U = U r , ^ _rr = ^σ φφ               τ r^∗r               ^τ φ^∗φ                m rrr                 ^m φφr

σ rr

" C33 (a) ^{, m} rφφ C 33 (a)a ^,

“ ^фф = c ₃₃ (a) ^, S ^rr = c ₃₃ (a) ^, S^ = c ₃₃ (a) ^, M ^rrr = c ₃₃ (a)a ^{, М ффг} = c ₃₃ (a)a ^{, М гфф} =

P = —, Pt = -pH , a = ¹, Bi ( € ) = -cH , B₂ ( € ) =      , B₃ ( € ) =      .

C 33 (a) ^, r       C 33 (a) ^, a ^{, 1}            C 33 (a) ^{, 2}           C 33 (a) ^{, 3}            C 33 (a)

Обезразмеренная постановка задачи градиентной теории упругости примет вид:

d Q _rr Q _rr -

7Г+  €

= 0 ,

M _rrr (1) = 0 , p r (1) = P.                              (13)

Здесь

Q rr

= S rr ^— € d€ ^{( €}M rrr ^{) +} € ^{( м} фгф ^{+ М} гфф) ,

^ ФФ = ^S фф —     ^{( €м} ффг ^{) — ( м} ФгФ ^{+ М} гФФ ⁾ ,

ξ dξ          ξ

Srr = B3 (€) dU + B2(€) U,  Sфф = B2 (€) dU + B1(€) U,  Mrrr = a2 d|rr dξ         ξ               dξ         ξ              dξ

М ффг = a ² dS^ , М гфф = M *r* = 1 a ^{2 ( S rr} ,^S** ) d^{€                        2          €}

P r (1) = {

S rr

-

€d€ ^{( €}M rrr ) ⁺ € ^{( м} ффг ^{+ М} фгф ^{+ М} гфф ) ^

В задаче (12), (13) физические характеристики цилиндра B 1 ( € ) , B 2 ( € ) , B 3 ( € ) являются функциями безразмерной радиальной координаты, в частности могут быть кусочнопостоянными в случае цилиндра с однородным покрытием или непрерывными, в случае, если покрытие изготовлено из функционально-градиентного материала (ФГМ).

Согласно классической теории упругости на поверхности сопряжения покрытия и цилиндра € = Ro должны выполняться условия непрерывности по перемещениям и радиальным напряжениям. В градиентной теории упругости на поверхности соединения цилиндра и покрытия согласно вариационному принципу [18] должны выполняться дополнительные условия сопряжения в виде непрерывности градиентов перемещений и моментных напряжений. Для упрощения расчетов примем градиентный параметр одинаковым для покрытия и цилиндра, т. е. ai = 02 = а. В случае двухслойного цилиндра постановка задачи (12), (13) согласно [18] преобразуется к виду:

(1)    Q(i) _ Q(i)          >о(2)    Q(2) _ Q(2)

d /'    ^         d de + e       0,    de + e u,

U ⁽¹⁾ ( R o ) = U ⁽²⁾ ( R o ) ,   due ¹) ( R o ) = dU, ² ( R o ) ,

Mrrr (Ro) = Mrrr (Ro),  pi (Ro )= W') (Ro),(15)

M^rr (1) = 0,   ;   (1) = P,(16)

где R o = ra — поверхность сопряжения.

• 4.    Решение задачи

Цель исследования состоит в нахождении НДС цилиндра с покрытием, как в случае однородного покрытия, так и сделанного из ФГМ.

В [15] были получены точные аналитические выражения для радиальных перемещений однородного изотропного сплошного цилиндра, содержащие модифицированные функции Бесселя. Выяснено, что в этом случае градиентных эффектов не возникает. Исследуем возможные градиентные эффекты в случае сплошного электропругого цилиндра с покрытием. В качестве первой задачи рассмотрим нахождение перемещений цилиндра U ⁽ⁱ⁾ ( e ) и покрытия U ⁽²⁾ ( e ) в случае, если цилиндр и покрытие изготовлены из однородных материалов. Для этого уравнения равновесия (14), условия сопряжения (15) и граничные условия (16) выражаются через перемещения, а физические характеристики цилиндра и покрытия полагаются константами. В параграфе 3 выяснено, что постановка задачи для электроупругого цилиндра сводится к постановке задачи для анизотропного упругого цилиндра с модифицированными модулями упругости. Выполняя действия, аналогичные, как в работах [15, 18] для упругого изотропного цилиндра, с учетом ограниченности решения в точке e = 0 , получим решение задачи (14)-(16) в виде:

u ⁽ⁱ⁾ = D i e m ¹ + D 2 I 1 (m^) , u ⁽²⁾ = De m 2 + D 4 e ^{- m} 2 + D 5 I 1 ( mOe ) + d ₆ K i ( moi ) .

Здесь I i ( ml^ ) , K i ( mO^) — модифицированные функции Бесселя первого и второго рода /в^¹) /В!²)

первого порядка соответственно, m i = J в1ду , m 2 = Ы в 12) .

В выражениях (17) константы D i ,..., D 6 определяются путем удовлетворения условий сопряжения (15) и граничных условий (16). После нахождения перемещений далее аналитически определяются напряжения Коши S _rr и S φφ , моментные напряжения M _rrr , М фф_г , М _гфф и полные напряжения Q rr , ^ фф для каждого из слоев.

В качестве второй задачи рассмотрим нахождение НДС цилиндра с покрытием в случае, если покрытие изготовлено из ФГМ с непрерывным изменением модифицированных модулей упругости через поверхность сопряжения. В этом случае возможно лишь численное решение задачи (12), (13), например, методом пристрелки.

Для решения задачи методом пристрелки после некоторых преобразований уравнений получим каноническую систему 4 обыкновенных дифференциальных уравнений (ОДУ) 1-го порядка относительно функций U i = U , U 2 = S rr , U 3 = S ‘ rr , U 4 = p r

U ‘1 = В3 U2 — |(

U ‘2 = U3'(19)

U ‘3 = - A U4 - i (bi - B) U + ('. (1 - B)) U2 - £■(20)

α2      ξ2        B1 ξ α2 ξ2      B3

u‘4=-1^+(1+a2)(ii -B2) Ui+1 ((1+a2) B2 - a2) U2.(21)

ξ ξ2       ξ2          B1 ξ        ξ2 B3

Здесь знак «штрих» обозначает производную по координате ξ.

Граничные условия примут вид

Ui«a)=0' U3(^o) = D, U3(1)=0, U4(1)= P.(22)

Первые два условия в (22) в силу ограниченности решения являются дополнительными граничными условиями в точке С = С о , достаточно близкой к нулю.

Согласно методу пристрелки, решение краевой задачи (12), (13) можно представить в виде суммы решений двух вспомогательных задач Коши:

U i = P 1 U I (0+ P ^ U I «)' i = 1 ,..., 4 .                       (23)

Каждая из вспомогательных задач состоит из канонической системы ОДУ (18)–(21) с одним из следующих наборов условий в точке ξ 0 :

• 1)    U I ( С о ) = 0 , U I ( С о ) = 1 , U I ( С о ) = 0 , U 4 «0 ) = 0 ;

• 2)    U I¹ ( С о ) = 0 , U" ( С о ) = 0 , U^ ( С о ) = 0 , U I¹ ( С о ) = 1 .

• 5.    Результаты вычислений

Константы p 1 и p 2 , входящие в формулу (23), находятся путем удовлетворения двух последних условий (22) на боковой поверхности цилиндра.

При наличии у функций B i ( С ) , B 2 ( С ) , B 3 ( С ) разрыва 1-го рода на поверхности С = R о осуществлялось решение задач Коши на интервале [ С о ,R о ] , а затем согласно [26], посчитанные решения в точке С = R о задавались как условия для задач Коши, которые затем решались на интервале [ R о , 1] .

Рассмотрим результаты вычислений распределения по координате ξ безразмерных перемещений, напряжений Коши и моментных напряжений двухслойного пьезокерамического цилиндра при P = 1 , R о = 0 . 7 .

В первой серии вычислений покрытие полагалось однородным, при этом модифицированные модули упругости полагались равными: B ⁽ⁱ⁾ = B ⁽ⁱ⁾ = l 3ⁱ⁾ = 0 . 25 , B ⁽²⁾ = B ⁽²⁾ = B 32) = 1 . Вычисление перемещений производилось по формуле (17).

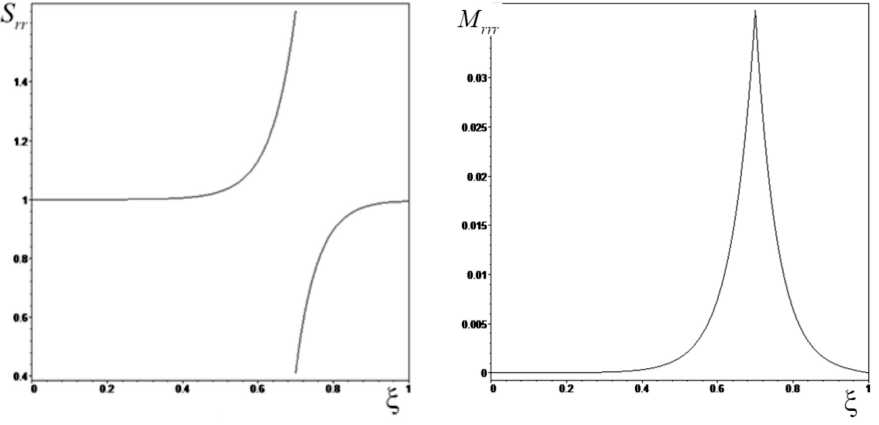
На рис. 1 а показано распределение по координате ξ радиальных напряжений Коши S rr , а на рис. 1б моментных напряжений M rrr , вычисленных при a = 0 . 06 .

a)                                                               б)

Рис. 1. Распределение по координате ξ: а) S rr ; б) M rrr .

Из рис. 1 следует, что: 1) радиальные напряжения Коши на границе сопряжения терпят разрыв, что связано с разностью электромеханических характеристик и непрерывностью перемещений и их первых производных на поверхности сопряжения; 2) моментные напряжения принимают пиковое значение на поверхности сопряжения.

На рис. 2 показан результат вычисления по формулам (17) радиального распределения смещений. При этом сплошной линией показано решение задачи в классической постановке при а = 0 , точками — в градиентной постановке при а = 0 . 06 .

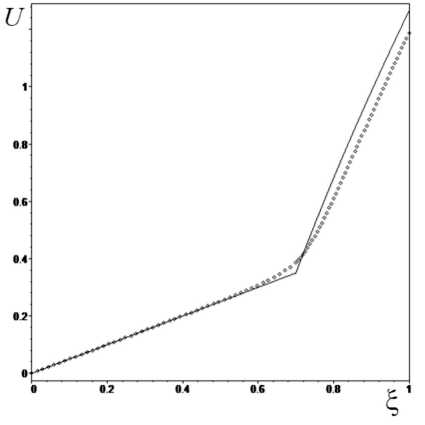
Рис. 2. Распределение перемещения по радиальной координате, когда покрытие однородное.

Из рис. 2 следует, что при решении задачи в градиентной постановке наблюдается: 1) более гладкое распределение радиальных перемещений в окрестности сопряжения; 2) уменьшение значений радиальных перемещений по сравнению с классической постановкой.

Во второй серии вычислений покрытие полагалось неоднородным, а вычисления производились на основе метода пристрелки при £ д = 0 . 001 .

Исследовано влияние величины масштабного параметра α на точность вычисления безразмерных перемещений численно методом пристрелки путем сравнения с аналитическим решением по формулам (17). Выяснено, что погрешность вычисления перемещений на боковой поверхности цилиндра £ = 1 методом пристрелки не превосходит 2% при а >  0 . 05 .

В случае покрытия из ФГМ в расчетах положим материальные характеристики цилиндра B ⁽¹⁾ = B ^¹) = B g¹) = 0 . 25 , B ⁽²⁾ = b 2² = B g²) = 1 , а законы неоднородности модифицированных модулей покрытия B ⁽²⁾ ( £ ) = B ^² ( £ ) = B g²) ( £ ) = 1 + (10 ^ — 7) N , что обеспечивает непрерывное изменение материальных характеристик через поверхность сопряжения.

Проведено исследование влияния двух различных законов неоднородности, характеризующихся параметром N , на распределение радиальных перемещений. На рис. 3 показано радиальное распределение перемещений при а = 0 . 06 и показателях неоднородности N = 1 (сплошная линия), N = 2 (точки).

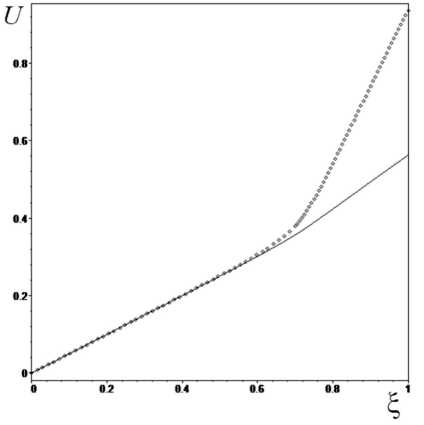
Рис. 3. Распределение перемещения по радиальной координате при разных значениях параметра неоднородности N .

Из рис. 3 следует, что с увеличением параметра N значения перемещений увеличиваются.

• 6.    Заключение

Исследована задача о деформировании сплошного радиально-поляризованного цилиндра с покрытием под действием постоянной нормальной механической нагрузки на боковой поверхности. Задача сведена к задаче градиентной теории упругости с ужесточенными модулями упругости. В случае однородного покрытия получены точные аналитические выражения для нахождения радиальных перемещений и напряжений. В случае функционально-градиентного покрытия решение построено на основе метода пристрелки. Показано отличие распределения перемещений и напряжений по радиальной координате, рассчитанных по классической теории и по градиентной теории электроупругости.

Выяснено, что 1) увеличение масштабного параметра снижает значения радиальных перемещений и полных окружных напряжений; 2) на поверхности сопряжения цилиндра с покрытием радиальные напряжения Коши терпят скачок, обусловленный непрерывностью градиентов перемещений; 3) радиальные моментные напряжения во много раз меньше напряжений Коши и принимают пиковое значение на поверхности сопряжения.