Математическая модель баллистического летательного аппарата с переменными массогеометрическими характеристиками

Движение летательных аппаратов (ЛА) в атмосфере определяется гравитационным полем Земли, воздействием набегающего атмосферного потока на наружную поверхность (НП) ЛА, массогеометрическими характеристиками (МГХ) ЛА – массой, координатами центра масс (ЦМ), значениями осевых и центробежных моментов инерции. Геометрические характеристики НП ЛА, взаимное расположение конструктивных элементов и составных частей ЛА определяются в конструкторской документации и описываются в конструкторской системе координат (КСК). В частности, для баллистических ЛА (БЛА) начало КСК помещают в точке O (рис. 1), положение которой привязано к конструктивным элементам летательного аппарата (например, лежит в плоскости одного из шпангоутов и является центром окружности расположения осей базирующих штифтовых отверстий). Ось OX_o (рис. 1) КСК направлена к носку БЛА и перпендикулярна плоскости базового шпангоута, ось OY_o перпендикулярна оси OX_o и расположена в плоскости ориентации I–III БЛА, ось OZ_o дополняет тройку осей до правой. Для рассматриваемого класса БЛА номинальное положение оси OX_o КСК совпадает с осью симметрии его наружной поверхности.

В процессе изготовления летательного аппарата возникают случайные отклонения геометрических характеристик НП и МГХ БЛА от заданных в конструкторской документации значений. Во время полета в результате взаимодействия с высокоскоростным, высокотемпературным атмосферным потоком возможно изменение геометрии НП и МГХ БЛА.

Отклонение реальных параметров БЛА от их допустимых диапазонов значений во время движения может привести к формированию возмущенной траектория полета БЛА.

IV

O

O

XG

G

I

C

Y G

Z G

X C

P

C

Z P

Y P

XP

Рис. 1. Основные системы координат, используемые для построения математической модели

Математическая модель БЛА с переменными МГХ

Рассмотрим модель БЛА как систему двух тел, имеющую внутренние связи и допускающую взаимные перемещения тел, входящих в нее. В качестве первого тела (платформы) примем корпус БЛА, в качестве второго - полезный груз (ПГ).

Начало связанной с БЛА опорной системой координат (ОСК) - полюс P совпадает с номинальным положением ЦМ БЛА, заданным в КСК OX o Y o Z o . Направление осей ОСК совпадает с номинальным направлением осей КСК БЛА. В ОСК определена главная центральная система координат (ГЦСК) БЛА CX c Y c Z c , где C - центр масс БЛА. Движение полюса P рассматривается в инерциальной, геоцентрической СК GX G Y G Z G (рис. 1). Угловое расположение ОСК, связанной с корпусом ЛА, относительно СК GX G Y G Z G задается тремя углами Крылова (тангажа ф , крена П и рыскания ^ ).

Для независимого изменения всех МГХ изделия в сборе второе тело ПГ может изменять положение относительно платформы по трем линейным и трем угловым координатам. МГХ и аэродинамических характеристик (АХ) корпуса БЛА могут медленно меняться в полете в небольших пределах. Оценка закона изменения МГХ и АХ корпуса БЛА во время полета может быть получена на основании зависимостей, приведенных в [2].

В общем случае, для получения уравнений движения системы твердых тел можно использовать уравнения Лагранжа второго рода. В частности, такая процедура применяется при выводе уравнений движения механических систем роботов-манипуляторов [4]. В случае системы, состоящей из двух тел, имеющих в сумме двенадцать степеней свободы, математическая модель будет включать сорок восемь дифференциальных уравнений, определяющих траекторию движения системы. Для изучения точных моделей сложных систем тел с изменяющимися МГХ целесообразно использовать специализированные системы анализа динамики механических систем, такие как АДАМС, «Универсальные механизмы» и другие. Однако эффективность работы таких инструментов зависит от корректности определения начальных, граничных условий задачи, диапазона изменения параметров модели.

Для получения необходимых предварительных оценок воспользуемся подходом, описанным в [1], где для изучения поведения БЛА с медленно меняющимися МГХ используются уравнения движения свободного твердого тела.

Нормальная форма Коши системы уравнений (при условии независимости главного вектора и главного момента внешних сил от линейного и углового ускорений) может быть записана в матричной форме:

V_P = — £ F ^{( j} ) - Q V P - П ² р + P ( J ⁽ O ) + m P ²) ^{- 1} x [ ^ m P^j ) - P ^ F ⁽ j ) - Q J ⁽ O) n + M PQ ² р ]

, M j j j (1)

n = (J(P) + mP2)-1[£MPj) -P^ f(j) -QJ(O)Q + MPQ2р], j j где m - масса летательного аппарата, VP = [vPx, vPy, vPz ]r - вектор линейной скорости полюса P ОСК, VP = [vPx, vPy, vPz ]т - вектор линейного ускорения полюса P ОСК, F(j) = [F^j), Fj), F^j) ]T -главный вектор внешних аэродинамических сил, действующих на НП БЛА. Главный момент внешних аэродинамических сил, действующих на наружную поверхность БЛА, обусловленный асимметрией формы его НП и несовпадением точек ЦМ и центра давления, -MPj) = [mPX^, mP,), mP)]r . Вектор угловой скорости БЛА в ОСК - n = [nx, ny, nz ]r (nx = n, ny = £, nz =ф), где n, £, ф- углы ориентации ОСК БЛА относительно осей GXGYGZG. Вектор углового ускорения БЛА в ОСК - n = [nx,ny,nz]r. Угол атаки БЛА - ап =^2 +ф2 . Вектор положения ЦМ БЛА в его ОСК - р = [рx, рy, рz ]r,

Расчет и конструирование

-и Z

и

y

О_

^и Z

0 -и x

– матрица компонентов вектора угловой скорости БЛА,

- ^И у

и

x

-Р Z

Р у

Р= Р z

^{0 -р} x

– матрица компонентов вектора положения ЦМ в КСК,

-

^Р у

Р x

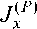
( P ) J_yx

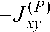
- J (P^P )

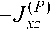
( P ) J_yz

- J Z^P )

J ( P ) =

– тензор инерции БЛА в КСК.

^^^^^^в

Левые части уравнений (1), а именно линейные и угловые ускорения определяются соотношением внешних силовых факторов, линейными и угловыми скоростями, а так же МГХ БЛА, записанными в правых частях уравнений. Возникающие отклонения аэродинамических сил и моментов БЛА от их проектных значений могут компенсироваться изменением МГХ и кинематических параметров БЛА. При этом левые части уравнений (1) могут сохранять проектные значения, что обеспечит движение по заданной траектории. В частности, в работе [5] рассматривается возможность использования разности смещений аэродинамического фокуса и ЦМ для определения эффективных плеч аэродинамических сил относительно оси вращения по крену.

Эта особенность законов движения ЛА используется на практике, в частности, в ЛА с «балансирной» схемой управления (дельтапланы, парапланы). Известны также схемы управления движением БЛА путем изменения продольной координаты его центра масс в сочетании с созданием управляющих аэродинамических моментов с помощью газодинамических рулей. Во всех этих схемах специальными способами, заложенными в конструкции ЛА, изменяется взаимное положение центра масс ЛА и точки приведения главного вектора аэродинамических сил.

Дополним уравнения (1) выражениями, определяющими МГХ системы, через МГХ составляющих ее тел. Прежде всего, определим дополнительные системы координат (рис. 2) – подвижную относительно ОСК главную центральную систему координат (ГЦСК) ПГ LX _lY_l Z_l и неподвижную относительно ОСК, ГЦСК корпуса KX_kY_kZ_k .

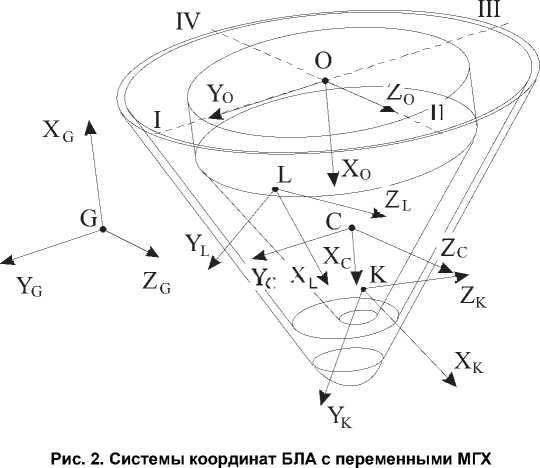
Положение ГЦСК ПГ и корпуса относительно ОСК заданы углами Крылова ф l , n l , ^ l , Ф _к, n _к, ^ _к и векторами р _к, р l , определяющим положение точек ЦМ L и K в ОСК. Положим, что вследствие малости возникающих на этапе производства и во время полета асимметрий распределения массы в ОСК, возможные потребные перемещения ПГ относительно корпуса малы. Обозначим также: M k , M l - массы корпуса и ПГ, M = M k + M l - масса изделия в сборе, J ^{( к} ) , J ⁽ l ) - тензоры инерции корпуса и ПГ в ОСК, J ⁽ p ) - тензор инерции летательного аппарата в ОСК. Кроме того, определим следующие ограничения: J Yир = J_Zup , J Xир <  0,1 J_Z ир , |8 J | <  0,01 J П .

Тензоры инерции J ⁽ p ) , J ^{( к} ) , J ⁽ l ) БЛА, корпуса и ПГ относительно ОСК, по теореме Гюйгенса-Штейнера [1, 3] определяются формулами:

J ⁽ p ) = A^T T J ^{( С} ) А с + M ( E р с ² -р с р с ) ;

J ^{( к )} = A ^T J ^{( K )} А . + M_k ( E р к ² -р к р _к ) ;

J(1) = ATJ(L) А, + Mi (E р i2 -р i р i), где J(С), J( p )- тензоры инерции БЛА в ГЦСК и ОСК соответственно, рс = [хс, Ус, zc ]T - радиус-вектор точки С ЦМ БЛА в ОСК,

J(K), J(к \ J(L), J(1 ’- тензоры инерции корпуса и ПГ в ГЦСК и ЦСК соответственно, рк = [xk, ук, zk ]т , рl = [xl, yl, zl ]T - радиус-векторы точек K и L ЦМ корпуса и ПГ в ОСК, р2 = x2 + У2 + Z2, рк = xk + Ук + zk, р2 = x2 + У2 + z2 - скалярные квадраты, рсрс, рi рi, ркрк - диадные произведения,

Ас, Ак, Al - матрицы преобразования координат БЛА, корпуса и ПГ из ЦСК (оси которых параллельны осям ОСК) в ГЦСК, составленные из направляющих косинусов осей, соответствующих ГЦСК в ЦСК, которые являются функциями трех углов Крылова ф,n,^, Фк, nк, ^к, Фl,Пl, ^l:

	( c	c	c		k	k	k		l	l	l
	a 11	a 12	a 13		a 11	a 12	a 13		a 11	a 12	a 13
А =	c a 21	c a 22	c a 23	, А к =	ak 21	O ’ 22	a ’ 23	, A l =	l a 21	l a 22	l a 23
	c	c	c		k	k	k		l	l	„ l
	( a 31	a 32	a 33 J		( a 31	a 32	a 33 J		( a 31	a 32	a 33 J

Радиус-вектор центра масс р с изделия в сборе может быть определен, как функция радиус - сс  с a 11 = 1 a 12 = ф, a 13 = -^ , ас21 = -Ф, ас22 = 1, ас23 = n , сс  с a 31 = ^, a 32 = -Л, a 33 = 1.

ak 11 = 1, a" 12 =Фк, a" 13 = ^к ’ kkk a 21 = -Фк, a 22 = 1, a 23 = nк, a 31 = ^к, a 32 = -nк, a 33 = 1.

a ^l 11 = 1, a l 12 = ^Ф l , a l 13 = -^ l , a 21 = - ^Ф l , a 22 = 1, a 23 = ⁿ l , a 31 = ^ l , a 32 = - ⁿ l , a 33 = 1.

векторов центров масс в ОСК и масс, составляющих изделие элементов:

M	M	M	M	MM	M Zc =-- Lzk M k 0 0	M + —L Z/ M l
рс = -р! + — р>, или x =—- MkMl       M Тензор инерции БЛА, корпуса и Г J xС )    0 0 1			х к + — x ,, yc = —- у , +—- У; , kMl      MkMl 1Г в их ГЦСК соответственно: J xK )    0     0 1         Г J xL )
J ( С ) = 0 0	J УС ) 0	0 , J ( K ) = J ZС ) j	0 J yK ) 0 0	0 , J ( L ) = 0 J ZK ) j         [ 0	J yL ) 0 0 J zL ) _	.

Вследствие малости величин углов ф , n , ^ , ф _к , n _к , ^ _к , Ф l , n l , ^ l (менее 5 градусов), выражения для компонент матриц преобразования координат можно упростить [1]:

Выражения для компонентов тензоров инерции БЛА, корпуса и ПГ в их соответствующих ЦСК с учетом допущений также существенно упростятся: J^с x = J^С X , J^с_y = J^C Y , J^с_z = J^С_Z ,

^J xy = ^Ф ( ^{J С} X ^{- J} ^Y ) , ^J xz =^ ( ^{J С} Z ^{- J С} X ) , ^J yz = ⁿ ( ^{J С} Z ^{- J C}Y ) ,

Расчет и конструирование lLlLlLl x - J X, J у - J Y, J z - J Z, J xy

^-ф l ( J LX ^- J LY ) , J lxz “£ I ( J LZ ^- J LX ) ,

lLLкКкКкКкКК

^J yz ^-n l ( J Z ^J Y ) , J x ^- J X , J y ^- J Y , ^J z ^- J Z , J xy ^-ф к ( J X J Y ) ,

J к xz - ^ к ( J К Z - J К X ) , J к yz - П k ( J К Z - J ^KY ) •

Выражения для J ^{( p} ) , J ^{( 1} ) , J ⁽ к ) , M ( E p с ² -p с p с )

M k ( E P k ^{2 -} P k P k ) , M l ( E P l ^{2 -} P l P l )

можно

представить в виде:

J ^L

-ф l (JL

^J LY )

^ф l ( ^J LX ^J LY )

J ^L

-^ l ( ^jLz

'Пl ( JLZ - JLY )

J ^P

-I

■ Ф (JP

^J PY )

J ⁽ p ) -

-ф

( J^PX - J PY )

J

P

Z

-n

( JPZ - JPY )

J ^К

-ф к ( JК

J

К

-Ф к

J К Y )

J

• ^- 5 l ( ^J Lz ^{- J} LX )

• - nl ( JLZ - JLY ) ;

^{j L}Z      .

• - ^ ( ^J PZ ^{- J} PX )

• - n (JPZ - JPY ) ;

J PZ      .

Y ) ^ к ( J К z - J К X )

• - n к ( J К Z - J К Y )

-^к (J ГZ - JГX ) -n к ( JКZ - JК Y )

К

Z

M ( E P с 2 -P с P с )-

^M ( У с ² + z c ) - M x_c y_c - M x_c z_c

- M x_c y_c    - M x_c z_c

^M ( ^x c + ^z c )   ^{- M} У с ^z c   ;

2 2\

^{- M} с ^y_c , ^z_c^M с ( ^x _c + ^yc )

Mk ( EP k 2 -P k P k )-

Ml ( E P l2 -P l P l )-

^M k ( У к ² + z 2 ^{- M} k ^X к Ук

^{- M} k x k zK

Ml (y2 + zf)

^- Mlxiyi

^- M l x l z l

)  ^{- M} k ^x K У к    ^{- M} k ^x K ^z K

^M k ( x ² + z ² )   ^{- M} k y K ^z K

• ^- M k y K , ^z K ^M k ( x ² + y k )

• ^- M l x l y l     ^- M l x l z l

2 2

^M l ( x l + ^z l )   ^- Miyizi    •

2 2

^{- M} l y l , ^zl    ^M l ( x l + y l )

Тензор инерции J ^{( p} ) БЛА в его ОСК может быть определен через тензоры инерции ПГ J ^{( l} ) и корпуса J ⁽ K ) , в соответствующих ГЦСК, по следующей зависимости:

j ^{( p} ) - A T j ⁽ K ) A_k + M k ( e p k ² -p _k p k ) + A T j ^{( l} ) A l + M l ( e p i ² -P i p i ) .

Компоненты J ^{( p} ) , а именно J xy ^{( p} ) , J_xz ^{( p} ) , J_yz ^{( p} ) , могут быть записаны в виде:

^Jxy ^{( p} ) ^{- ф} ( ^jPX ^{- J}PY ) ^{+ M} x c yc ^{- ф} l ( ^jlX ^{- jl}Y ) ^{+ ф} к ( ^JКX ^{- J}КY ) ⁺ M k x k^ук ^{+ M}l^xl ^yl ^;

^Jxz ⁽ p ) ^- ^ ( ^JPZ ^{- J}PX ) ^{+ M} x c ^zc ^- ^ l ( ^jlZ ^{- jl}X ) ⁺ ^ к ( ^JКZ ^{- J}КX ) ^{+ M}k^xK ^zK ⁺ M l x l ^zl ;

^Jyz ^{( P} ) ^-n ( ^JPZ ^{- J}PY )^{+ M} y c z c ^-n l ( ^jlZ ^{- jl}Y ) ^{+ n} K ( ^JКZ ^{- J}КY ) ⁺ M k y K ^z k ^{+ M}l^yl^zl •

Положим, что на начальном участке движения в атмосфере БЛА не имеет асимметрий формы НП и МГХ. Такое состояние достигается высокоточной обработкой НП БЛА и проведением коррекции МГХ изделия на специализированном оборудовании относительно прогнозируемого направления равнодействующей вектора аэродинамических сил. В результате выполнения этой процедуры все МГХ БЛА имеют допустимые значения. В «идеальном» состоянии БЛА войдет в атмосферу с близкими к нулю углами атаки, что обеспечит ему на начальном участке траектории малые значения угловых скоростей и угловых ускорений вдоль поперечных осей координат. По мере нарушения симметрии НП, отклонения параметров НП и МГХ изделия будут постепенно нарастать, симметрия обтекания нарушится и изделие приобретет угловые тлx, таy, таZ и линейные VPx, VPy, VPz ускорения. В течение достаточно малого интервала времени ускорения не приведут к значительному изменению линейных и угловых скоростей VPz , VPy, таx, таy , таZ. Запишем упрощенные выражения, связывающие вторые производные параметров движения и МГХ БЛА, с учетом особенностей движения изначально «симметричного» изделия, пренебрегая таyтаx, таyтаz , таxтаz , та2, та2, таy , таyVPZ , таZVPy, таxVpz

сти и полагая J P = J P yz

P

z

, та _xV_Py как величинами второго порядка мало- 1 = J - JP\ = J P п .

Получим выражения, связывающие текущие значения ускорений с р l , ф l , n l , ^ l .

(Mk z, та у + —-yk + —Ly, та z ;

l J I M У J

• V Px	=—y F j ) — 1 M jx	I M^z { M k	M + — l. M
• V Py	j )- m 2 1 y	I Mk k x ( M k	M + — l M
• V Pz	=—y F z) j ) — I M j Z 1	I Mk k yk V M	M + — l M

■   IMk    Ml Утаz + —-zk + —Lz/ та,;

I M M l J ^x

У  (Mk   Mt у yi 1та x+1 yxk+M^xi 1та у;

( j ) _f ^M-L_v . ^M l , ■ )y F⁽ j ) + f +^Ml -z ^У jj ) m_PY — y + y? f +       z^ + Zi

у Px ( M k M l J j Z ( M k M l J j y та x =

в

^ i ( J LZ

Z

^: К z k ^{+ M} l x l ^Z i

в

xkzk

1 — ^M ^ I M_k — ( x_kz_t M J k ^k

_{— xz} ^M k M ^l k ) M

1 - M^ | M M J ¹

■

та

z

в

^х л ^;

в

^J К x ) ^{— M} k x k y_K ^{— M} i x i y i

в

+ ^х к У к ¹

Mk          \MM

--k- Ш_к — x_ky, — x, y_k —k—‘-k kl lk

+ ^х 1 У 1 ¹

в

Ml bz l _M

M J ¹

та

У _т ( j ) _| ^M k - , ^Ml - 7 m_p — ---- Z r + Zi

^Py I M ^k M ¹

M k M l xF ⁺

MkM

та у =

фl ( JLY — JLX ) + ФК ( J

+

^{+ х} к У к ¹ -

^{— J} КX )^{— M} k ^X K ^y

MM

■i ^— x i ^y k ) ^ M^

’ К ^{— M} l x i y i ⁺

⁺ x i y i 1 ^{1 — М} I ^M i M J

та

^х J^p ’ J_y

Расчет и конструирование

^TO z

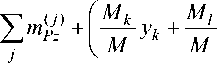
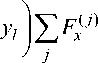
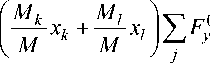
^{+ M} k ^X K z K ⁺ M l x l z l ^-

Ч l ( JLZ - J ) + ^ к ( J К Z - J К X )

^- xkzk V

Mk U /

M k I M k ⁺( x k z i ^- x i z k

M k M l ' M

^- x l z l

1 - M l - I M_t

M I ¹

TO x

^x jp-

Полученные выражения могут использоваться для получения оценок значений кинематических параметров и их производных в зависимости от взаимного положения груза относительно платформы БЛА.