Математическая модель биологического реактора

Культивирование клеток тканей и микроорганизмов осуществляется в биологических реакторах. Биологические реакторы самой разной конструкции применяются в пищевой промышленности, медицине, экологии и других областях деятельности человека. Конструкции реакторов разрабатываются для решения конкретных технологий выращивания микроорганизмов [1]. Рассматривается проточный реактор непрерывного действия, в котором выращивается биомасса на субстрате. При больших концентрациях субстрата возможно субстратное угнетение удельной скорости роста биомассы. При превышении скорости поступления субстрата порогового

значения возможно вымывание биомассы из реактора.

Математическая модель биологического реактора

Пусть в реакторе длиной l выращивается биомасса X на субстрате Y , поступающем в реактор со скоростью V [1, 2]. С этой же скоростью продукты удаляются из реактора. Система уравнений, описывающая рост биомассы на лимитирующем субстрате с учетом субстратного угнетении при наличии диффузии субстрата и биомассы, имеет вид (в нормированном виде) [2, 3]

дX  _ д2 X  дXXY

— = D—г - v— +у д t     дx2    дx  1 + Y + gY2

д Y  ^д2 Y д YXY

— = D—у - vу, д t     дx2    дx  1 + Y + gY2

где g - параметр, характеризующий ингибирование, D - коэффициент диффузии, V -скорость поступления субстрата в реактор и скорость выхода биомассы, X - концентрация биомассы, Y - концентрация субстрата.

В (1)

XY

1 + Y + gY2

- скорость роста биомассы и, соответственно, скорость убыли суб

страта.

К системе уравнений (1) добавляются начальные условия

X (t = 0) = X0, Y (t = 0) = Y,(2)

и граничные условия при x = 0: X = 0, Y = У0,

1 9X  n 5 Yn при x = l: ---= 0, — = 0.

dxd

Граничные и начальные условия предполагают, что в начальный момент времени в реактор загружены биомасса и субстрат, а извне в реактор поступает только субстрат.

Реактор идеального смешения

Для случая реактора идеального смешения система уравнений (1) с учетом граничных условий (3)-(4) и начальных условий (2) принимают вид

dX dt

—vX +

XY

1 + Y + gY2,

dY dt

v (Y — Y0) —

XY

1 + Y + gY2 ’

X ( t = 0) = X 0 , Y(t = 0) = Y 0 .

Решением этой задачи Коши является первый интеграл

X (t) + Y (t) = Y0 + (Xo + Y — Y0) e—vt.

Из этого выражения следует, что в стационарных точках X + Y = Y ⁰ .

Особые точки уравнений (5) удовлетворяют системе уравнений

X + Y = Y °, которая всегда имеет решение X = 0, Y = Y. Функция

Y

f (Y) =----------2

1 + Y + gY2

имеет экстремум равный v

-----при Y = —;=. Соответственно при v <  v_max

1 + 2V g         gg                       max уравнения (6) будут иметь еще два решения:

Y2 = -1-(1 - v - V(1 - v)2 - 4gv2), X2 = Y° - Y ,

2gv

Y3 = 1-(1 - v + V(1 - v)2 -4gv2 ), Xз = Y° - Y3.

2gv

Матрица Якоби системы (5)

'-v + f (Y),    Xf '(Y) '

I -f(Y),   -v- Xf'(Y))

имеет собственные значения

Л1 = -v, Л2 = -v - Xf '(Y) + f (Y).

В точке притяжения X = 0 , Y = Y ⁰. При выполнении неравенства v <  v _maх будет положительным Л ₂, и отрицательным - при v >  v_maх . Последнее неравенство обеспечивает устойчивость этой точки.

Во второй (7) и третьей (8) точках притяжения ^ = - Xf '(Y ) . Поскольку точка (7) лежит слева от точки максимума функции f(Y ) , то в этой точке А ₂ принимает отрицательное значение, а в точке (8) – положительное. Поэтому при выполнении неравенства v <  v _max устойчивой является вторая стационарная точка.

Таким образом, при выполнении неравенства v >  v_max существует только одна стационарная точка с нулевым значением X . То есть при больших скоростях поступления субстрата в реактор должно происходить «вымывание» биомассы из реактора.

Реактор неидеального смешения

Для диффузионной модели (1) установившееся распределение X = X ( X ) и Y = Y ( X ) находится из уравнений

d2X dXXY

= 0 ,

D--Т - v--+у dX    dx 1 + Y + gY2

d2Y dYXY

D--у - vу dx2 dx 1 + Y + gY2

Система уравнений (9) с учетом (3) и (4) приводится к виду

Dd2Y-vdY- Y(Y°-Y) = ° dx2 dx 1 + Y + gY2    ’

X (x) + Y (x) = Y °,

0 dY с краевыми условиями Y(x = 0) = Yu , --- dx

= 0. Эта краевая задача имеет своим решением Y(x) = Y0. Удовлетворяющее граничным условиям решение уравнения в (10) можно представить в виде

Y (x) = Y0 + B sin | x.

Тогда с применением метода Бубнова-Галеркина из (10) будет получено уравнение для нахождения постоянной B

l

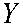
J 1 + Y + gY2

• 2 П x , n 2    ,1

sin--dx = —D + — v.

2 l       8l      2

Левая часть этого равенства ограничена сверху:

Y

1 + Y + gY"

•  2 П x ,  _

sin--dx < v

2l

l

. 2

Поэтому уравнение (10) решений иметь не будет, если выполняется неравенство vmax < v0

+ П D

4l

и, соответственно, тривиальное стационарное решение будет единственным. Последнее означает, что наличие диффузии понижает скорость «вымывания» биомассы.

Для случая значений параметров g = 2 и Y = 2 скорость вымывания в модели (5) v_maх = 0.26 . На рисунке приведена зависимость установившегося выхода биомассы из реактора в зависимости от скорости подачи субстрата (зависимость D = 0 ). Как следует из анализа полученных результатов, выход биомассы пропорционален скорости подачи субстрата, а вблизи критического значения скорости v = v_max происходит резкое падение выхода био-

массы. Численная реализация построения решений уравнений (1) и (5) осуществлялась в среде программирования математического пакета Matlab [4].

Выходу биомассы для диффузионной модели (1) для случая D = 0.05 на рисунке соответствует зависимость D = 0.05 . Расчетная скорость v_maх = 0.09 , а из неравенства (11) следует ее теоретическая оценка v _maх<  0.12 . Различие этих значение может быть вполне удовлетворительным для оценки влияния не идеальности перемешивания в биологических реакторах на стадии проектирования. Это необходимо учитывать в технологических процессах [5].

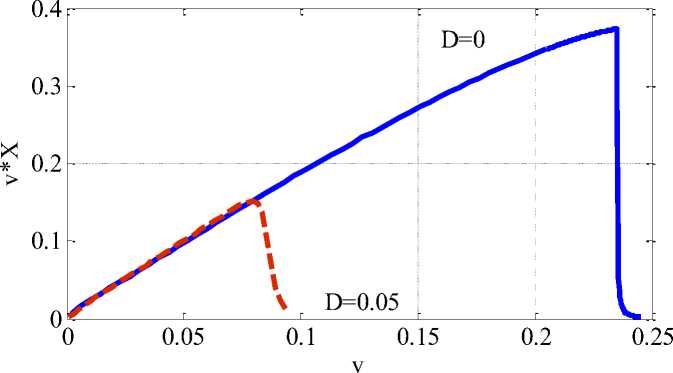
Рис. Зависимость выхода биомассы из реактора от скорости подачи субстрата

Заключение. Одна из задач производ-

скольку при больших скоростях возможно

ства – увеличение выпуска продукции при нерациональном регулировании технологического процесса может привести к потере части продукции. Для проточных биологических реакторов скорость подачи субстратов должна определяться исходя их кинетики биологических реакций, по-

понижение производительности реактора. Предельное значение скорости оценивается с учетом скорости роста биомассы. Возникновение диффузионных процессов приводит к уменьшению порогового значения скорости подачи субстрата.