Математическая модель деградационного разрушения контактных соединений полупроводникового прибора

является то, что величина долговечности не связывается непосредственно с физическими характеристиками структуры ПП и c воздействующими на них факторами режима эксплуатации.

В настоящей работе представлена математическая модель разрушения наиболее напряжённого (с точки зрения температурных условий) участка контактного паяного соединения в ППП, который в дальнейшем будем для краткости называть участком контактного соединения. Модель основана на кинетической термофлуктуационной теории прочности твёрдых тел [4]. Согласно этой теории, зависимость долговечности материала т(с,Т) от механического напряжения с и температуры T описывается форму -лой Журкова [5]:

т ( a ,T) = Т о exp

U( c ) k B T

где k B - постоянная Больцмана, U(о) = E d — ус – величина потенциального барьера активации процесса разрушения, E_D , – начальный потенциальный барьер процесса разрушения материала, у - коэффициент, характеризующий локальные перенапряжения в твёрдом теле, Т о - средний период колебаний атомов в твёрдых телах ® 10 -13 - 10 -12 сек.

Распад металлических связей в материале контактного соединения, находящегося под действием механического напряжения, описывается дифференциальным уравнением вида dn( x, y,t ) dt

= V r (1 — n(x,y,t)) — V D n(x,y,t) (2)

с начальным условием n(x,y, 0 ) = 1, где n(x,y,t) -относительная поверхностная плотность нера-зорванных связей материала соединения, определяемая как отношение поверхностной плотности неразорванных связей в некоторый момент времени к её начальному значению, v D , v_R - частоты процессов разрыва и рекомбинации (восстановления) связей материала, определяемые по формулам:

V D = т ₀ ¹ exp{ - [E D - уст • n(x,y,t))]/k_BT } ,(3)

V r = t - ¹ exp{ - [E D - yo o • n(x,y,t)]/k_BT} .(4)

Предположим, что по мере термофлуктуационных разрывов связей материала контактного соединения, нагрузка на соединение возрастает обратно пропорционально числу оставшихся связей, а коэффициент теплопроводности материала соединения уменьшается. Зависимости температуры перегрева контактного соединения и действующего механического напряжения от числа неразорванных связей материала соединения представим в следующем виде:

^ T(n) = ₇---- K ^A ' ^AT⁰-----.

⁷ {1 + (K _x- 1)n(x,y,t) } ’    ^(5а)

^V R

= ^t o ^{1 ex}P I^{- G} d '

1 -X ₀n ( x,y,t )

1+

KaA© o

[1 + (KA-1) n (x,y,t )]

. (8)

o(n) = oD < 1 +

( °D

-

A

- 1

V °o

1 n(x,y,t) >

, (5б)

где AT₀ = T - T_o - начальный перегрев контактного соединения; T₀ – температура окружающей среды; K a = A s / A sD - модельный коэффициент, определяемый как отношение начального коэффициента теплопроводности материала контактного соединения к минимальному эффективному коэффициенту теплопроводности участка контактного соединения; o₀ , o D - максимальное начальное термонапряжение и величина разрывной прочности материала контактного соединения соответственно.

Введём безразмерные величины

Для определения величины максимального начального перегрева структуры ППП необходимо решить нелинейную стационарную задачу теплопроводности, с соответствующими граничными условиями и температурозависимой плотностью мощности теплового источника, расположенного в активной области структуры. В качестве примера рассмотрим решение задачи разрушения контактного соединения кристалла с теплоотводом в мощном биполярном ВЧ транзисторе. Этапы решения задачи будут следующими:

1. Построение тепловой модели для полупроводниковой транзисторной структуры, представляющей собой трёхслойную среду: кристалл (C), припой (S), теплоотвод (H) (рис. 1). Источники тепла расположены в виде полосок на рабочей поверхности транзисторной структуры. Обычно толщина припоя много меньше толщины кристалла и теплоотвода S<< L zi , поэтому слой припоя рассматриваем как зону неидеального контакта, с термическим сопротивлением R_th .

Уравнения и граничные условия имеют вид: - уравнение теплопроводности

^Ti_a ^{+ T} i ^{+ T}i_zz = ⁰ , i = 1,2, (9) xx yy zz

( x , y , z ) e V = {( x , y , z ):0 <  x <  L x ,

⁰ <  y <  L y ,L_z (i - i) <  z <  L zi^}          ;

- граничные условия:

^T i_x ^(0,y^,z) = ^T i_x ^(L x ,y^,z) = ⁰ , (10)

Tiy(x,0,z) = Tiy(x,Ly,z) = 0 , (11)

G_d = -ED

^D k B T 0

,

X = ° , X = ^О 0 , ° D ,       ° D ’

А0

। = ^Те 0 , T₀

тогда соотношения (3) и (4), с учётом выражений (5а, 5б) и равенства yo D /E D = 1, будут выглядеть следующим образом

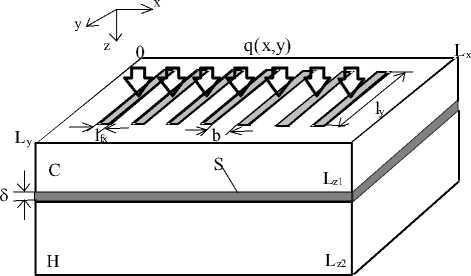
Рис. 1. Геометрия тепловой модели мощного СВЧ транзистора: C – кристалл (активная область эмиттера заштрихована), S - припой, H - теплоотвод

^v D = ^T0 1

exp ^{- G}d •

1 - [1+(xo1 -1)n(x-yt)]~

1 +     K a A0o

[1 + (KA -1) n(x,y,t )]

' . (7)

Л ! (xy-o) =

q^(x,y⁾, (x.y) e S ar

0, (x,y) e (S c - S ar ) ’ ⁽¹²⁾

^- ^ h ^T2_Z⁽ x.y.L z2 ) = ^a c ^T2⁽ x.y.L z2 ) , (13) где q(x,y) = j _b(T) • U b - плотность потока тепла, j_eb , U_сb - плотность эмиттерного тока и напряжение коллектор-база, S c = LL y , S ar = f • I f • l y - площади поверхности кристалла и его активной области соответственно, f – число полосок эмиттера, X c , X h - коэффициенты теплопроводности кристалла и теплоотвода соответственно, a c -коэффициент конвективного теплообмена с внешней средой;

• -    условия сопряжения в контактной области:

X _cT_Hz (x,y,L zi ) - X _hT₂ i z (x,y,L zi ) = 0, T 2 (x,y,L z ₁) - T₁(x,y,L z ₁) = =, R h X c T i_z (x,y,L_z i )

^(x>y) ^{e S} s = ^{(x,y) ^:0 ^ ^x ^ ^L x >° ^ y ^ L y } ,

(14) где R_th = d d / l l_s , S_s – термическое сопротивление и площадь контактной зоны соответственно;

• -    уравнение положительной обратной связи, учитывающее зависимость плотности потока тепла, выделяемого активной областью кристалла, от температуры

  q(x,y) = q o exp

  
  

(E g - eU eb + (e p /U cb ) • q^(x,y)) '^ kT                  I ’

(15) где U b - напряжение эмиттер - база, r r_d^ p = r• S r , , r - входное омическое сопротивление транзистора, E_g - ширина запрещённой зоны полупроводника, q₀ – слабо зависящий от температуры параметр, e - заряд электрона;

• -    условие постоянства средней плотности тока по активной области структуры

• 2.    Решение уравнения (9) при условиях (10) – (14) и постоянной плотностью теплового потока q(x,y) = q⁰ , которая принимается в качестве начального приближения итерационного процесса вычисления распределения температуры по структуре. Применяя интегральное косинус-преобразование Фурье к поставленной в п.1 задаче теплопроводности, получаем решение в виде ряда

  A T 0 (x,y,L z1 ) =

  
  

J(x,y ) = —— jj J(x,y )dxdy = const (16) S ar                                    .

S ar

^ года xcLxLy t==^m^ о

A nm B nm q nm

,

® cos( n n x /L_x )cos( m n y/L_y)

qnm = jjq(^,n)cos(nn§/Lx)cos(mnn/Ly)d§dn ,(17) Sc nm     nm(ggnm),     nm    nm(aac , ggnm, c, h, z1,

^L ₂ 2 ), Y nm = ( n ^{n /L} x ) ^{2 +} ( ^{m n /L} y ) 2 .

Для учета тепловой обратной связи необходимо совместное решение уравнений (15) и (17) при условии (16). Это решение находилось численным итерационным методом. Начальное зна- чение величины плотности теплового потока во всех точках структуры предполагалось одинаковым и равным q0, при этом средняя плотность тока определяется величиной рабочего тока I0 в структуре: j0 =I0 / Sar . Переменный шаг по напряжению Ueb на каждой итерации находился из условия сходимости алгоритма - (qr/qr-1)<1, где r – номер итерации

• 3.    Решение кинетического уравнения разрушения контактного соединения. Дифференциальное уравнение (2), с учётом выражений для частот разрушения и рекомбинации (7) и (8), решалось численным методом

Размеры полупроводниковой структуры соответствовали параметрам ВЧ транзистора типа КТ803: L x x L y x L_z = 4.8 x 4.8 x 0.45 мм; f x ( l fx x l y )=8 x (0.2 x 2.4) мм; толщина слоя припоя 55 = 0.02 мм. Электрофизические характеристики полупроводниковой структуры: E_g = 1.12 эВ, р п = 0.026 Ом ^ мм². Напряжение коллектор-база U_cb = 25 В, значение рассеиваемой мощности W = 10 – 50 Вт. Теплофизические и механические характеристики слоёв C и H структуры приведены в табл. 1 [6]. Величина модельного коэффициента K ^ определялась по формуле [7]

K x ¹ = (1 - P o )^1 - Р о , (18) где P₀ – значение пористости, соответствующее порогу перколяции. Процедура определения значения P₀ представлена ниже. Рассчитанные пределы изменений величины KX = 1.0 - 2.0. Диапазон значений безразмерной величины начального потенциального барьера принимался равным G_D = 80 – 150. Начальная температура T₀ = 300 K.

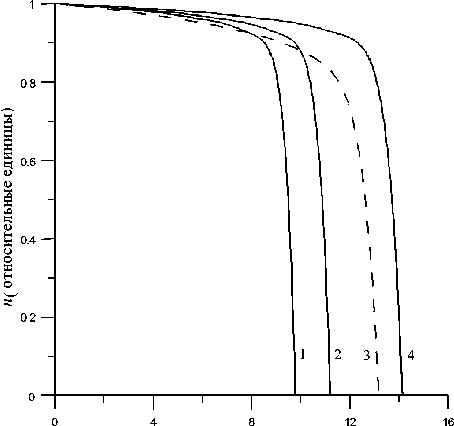
На рис. 2 представлены распределения безразмерных величин температуры перегрева и механического напряжения в контактной зоне кристалла и припоя ППП. Как уже упоминалось выше, дальнейшие расчёты долговечности контактного соединения проводились для его наиболее напряжённой точки, там, где температура Т и термонапряжение а 0 принимают максимальные значения. На рис. 3 показаны результаты численного решения дифференциального уравнения (2), при максимальных значениях безразмерных величин перегрева A0 m^a3C = 0.45 и термонапряжения £ 0 ^т<ас = 0.43. Модельная характеристика структуры G_D = 135 (эвтектика Au-Si). Характер кривых распада свя-

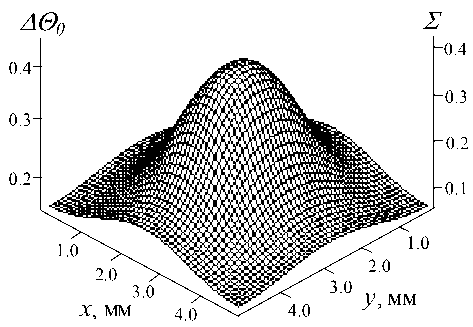
Рис. 2. Распределение величин перегрева и термонапряжения в слое припоя, W = 50 Вт, G_D = 135.

Таблица 1. Теплофизические и механические свойства материалов.

	λ , Вт/м ⋅ К	α , 10-6, град-1	ν	Ε , ГПа
Кристалл - Si	130	3	-	160
Теплоотвод – Cu	390	17	0,38	120

зей материала соединения будет аналогичным и для других значений параметров модели G_D и K_l . Критическое значение величины P₀ в выражении (18) определялось при помощи кривой распада n(t) для случая независимости величины перегрева контактного соединения от числа разорванных связей (кривая 3 рис. 3). Согласно этой кривой, переход процесса разрушения материала от фазы медленного спада к катастрофическому спаду происходит при n ≈ 0.8. Поэтому значение пористости выбиралось P₀ = 0.2, а со-

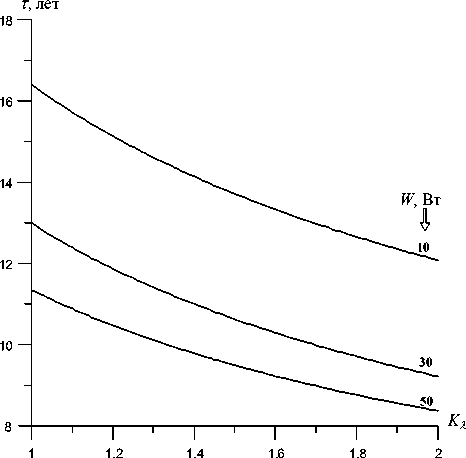
Рис. 4. Зависимость долголетия контактного соединения от модельного коэффициента относительной теплопроводности, G_D = 135

t , лет

Рис. 3. Кинетика распада связей контактного соединения, G_D = 135, K l _l = 1.4, W :

1 – 50, 2 и 3 – 30 , 4 – 10 Вт ответствующее значение коэффициента Kl = 1.4. По рассчитанным таким образом значениям порога перколяции, были получены зависимости величины долговечности контактного соединения от модельного коэффициента Kl, при различных значениях величины рассеиваемой мощности W (рис. 4). Для рассматриваемого варианта материала контактного соединения в ППП увеличение величины рассеиваемой мощности в 5 раз приводит к уменьшению долговечности ППП примерно в 1.44 раза, для всего диапазона изменения величины коэффициента Kl,. Нелинейность зависимости долговечности ППП от рассеиваемой мощности (рис. 5) определяется следующими причинами: 1) существованием положительной обратной связи между выделяемой активной областью кристалла плотностью потока тепла и температурой (см. выражение 15), которая приводит к нелинейной зависимости величины начального перегрева контактного соединения от рассеиваемой мощности; 2) введенными зависимостями (5а, 5б) величин перегрева контактного соединения и действующего термонапряжения от плотности оставшихся связей материала контактного соединения.

Представленная математическая модель дег-радационного разрушения контактных соединений в ППП, находящихся под длительным воз-

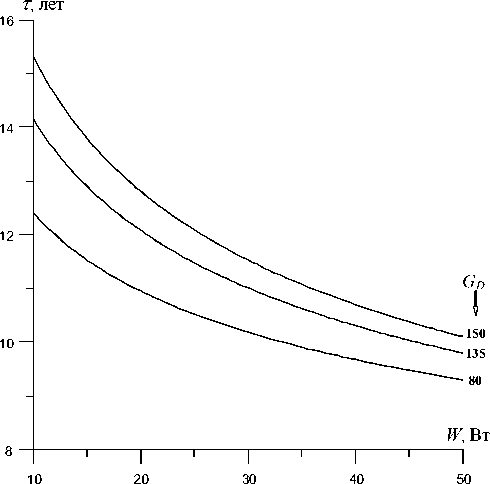
Рис. 5. Зависимость долголетия контактного соединения от рассеиваемой полупроводниковой структурой мощности, K l _l = 1.4

действием рассеиваемой мощности и приведённые результаты расчётов долговечности контактных соединений могут быть использованы для разработки методики оценки надёжности контактных соединений ППП с учетом усталостных эффектов и режимов его работы.

Работа выполнена в рамках проекта №2.1.2/ 4006 целевой программы Рособразования РФ “Развитие научного потенциала высшей школы (2009-2010) годы”.