Математическая модель динамики функционирования механизма привода утюга

В качестве объекта исследования выступает основной элемент данного типа технологического оборудования – механизм привода сварочного утюга. В его состав входят кулачково-коромысловый механизм, передаточное звено, тяговая цепь, пружина шагового транспортера, сварочный утюг, механизм отрезки пленки, клиперное устройство и другие элементы.

Для решения поставленной задачи необходимо описать физическую и математическую модели механизма привода утюга.

Механизм привода утюга будем рассматривать как голономную систему с одной степенью свободы, считая при этом, что связи в системе являются идеальными, а звенья механизма это абсолютно твердое тело. Тогда гибкие звенья, имеющиеся в механизме, можно считать всегда напряженными элементами, что позволяет отнести данные связи к двухстороннему виду. В качестве обобщенных координат системы принимаем угловую координату р и угловую скорость ср кулачка. Трением в шарнирах и колебанием утюга на пружине пренебрегаем. Последние допущения потребовали корректного обоснования, представляющего собой самостоятельную задачу.

За основу математической модели динамики функционирования механизма привода утюга выбрано дифференциальное уравнение движения. Для преобразования кинематических характеристик ведущих звеньев механизма в характеристики его ведомого звена в модель вводятся независящие операторы передачи движения, которые являются не зависящими от времени функциями [1,5].

Определение операторов передачи движения всех звеньев [2], входящих в данный механизм, начнем с кулачкового механизма.

Учитывая схему механизма привода утюга (рис.1), определим геометрические характеристики кулачкового механизма

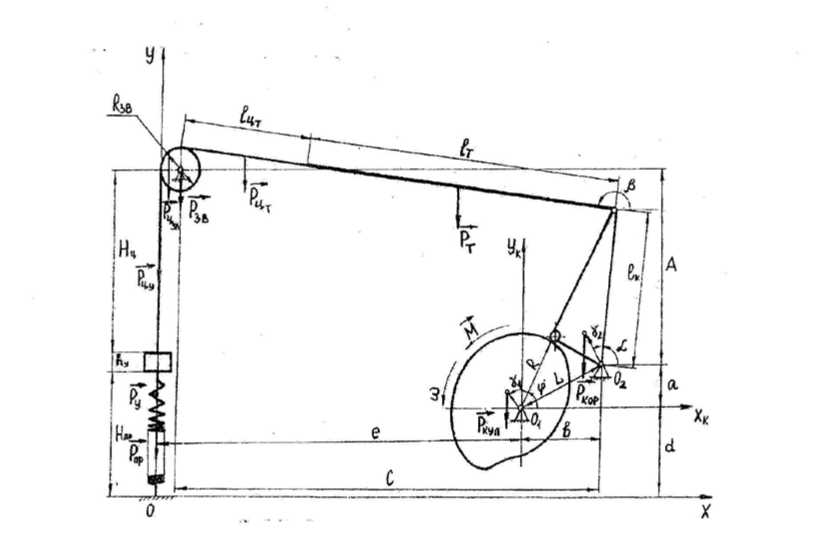
Рис. 1. Схема механизма привода утюга

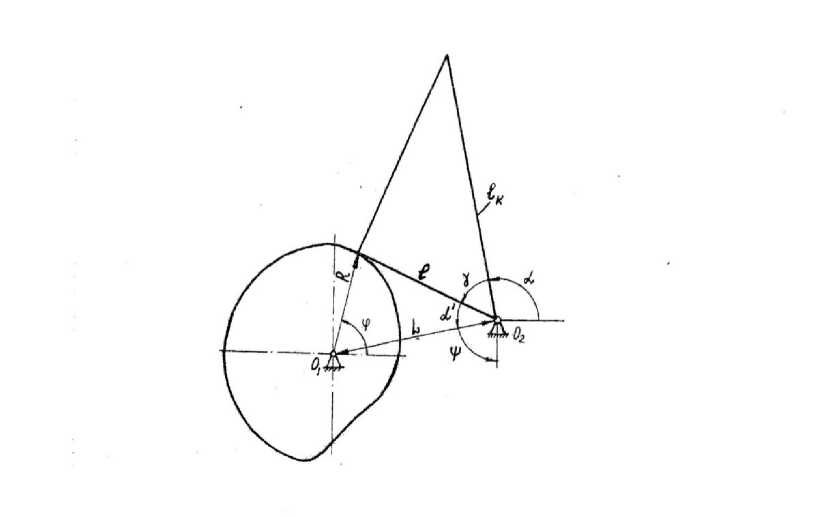
Рис. 2. Геометрические характеристики кулачкового механизма

В качестве ведущего звена в данном механизме выступает кулачок. Тогда справедливы следующие выражения для операторов передачи движения звеньев механизма.

Кулачок (рис. 2):

Угол поворота к=к                                    (1)*

скорость dv = 1 dϕ

ускорение

d^ = 0. dv

Коромысло (рис.2):

Угол поворота

a = 0 - arccos(

L ² + 1 ² - LIT

R ²

);

скорость

da = ,         2R         , dR dV     J4L212-(L2 +12 -R2)2 dV

ускорение d a dv2

Тяга угол поворота

d a ₍d ² R dR , dR J     2 R (L ² + 1 ² - R ²)

--{(—г / —) + — (---■ ■ — й—;-- vv) }• d v d dv ² d v    d v RR 4 L ² 1 ² -( L ² + 1 ² - R ² ) ²

скорость

ускорение

где скорость

A - l_K sin a в = n - arctg —¹-------- ;

C +l сosα к dβ dβ dα --- =---; dϕ dα dϕ d2в = d2в (da)2 + dp da da da2 dv    da dv2

dp _   l_K ( l_K - 4 1 sin a + Ccos a )

d a   ( C + l_Kcos a ) ² + ( A 1 - l_K sin a ) ² ’

(1)**

(1)***

ускорение d2 в = lK (l K 2 - A12 - C 2)(A1 cos a + C sin a) dv2 {(C +1K cos a)2 + (A1 -1K sin a)2}2 ’

где 4 = А + R_3B ;

• l_к – длина большого плеча коромысла, м;

• А, С - расстояние между осями вращения коромысла звездочки по осям ординат и абсцисс, мм;

R_ЗВ – радиус делительной окружности звездочки, м.

Цепь суммарная длина цепи

Н ц = ‘ ц + > Т + С + c a - n R . ;                    (10)

cos в 2

скорость dH dH d α

----ц- =----ц---;                                          (11) dϕ  dα dϕ ускорение

d2 H ц dp2 d2 Нц da2 dH d2 a ц (    )2 + ц da2 dp    da dp2 (12) где скорость H = 1 dp cos Q {(C + lk cos a)tgfi в 1к sin a}; в            da (13) ускорение d2 H ц da2 = ^KC - cos в -lK cosa){ в tge + ( в)2} lK cosa]; da      da (14) lц – длина цепи, м; lТ – длина тяги, м. Пружина общая длина пружины Нпр = Н,р 0 +(Нц 0 - Нц)                            (15) скорость dH ----пр =--ц-;                                      (16) dp    dp ускорение d2 Hnp    d2 Нц -----п— =--(17) dp2      dp2 где Нпр 0, Нц 0 - длина пружины и части цепи в момент, когда утюг находится в крайнем нижнем положении, м;

Н_ц – длина той же части цепи в текущий момент, м.

Приводной механизм

угол поворота pp =1 p;                                   (18)* i скорость dp„   1 = 1;                                       (18)** dp   i ускорение d 2p„ —P = 0                           (18)*** dp2 где i – передаточное число привода;

p _p - угловая координата ротора электродвигателя, рад.

Решая задачу по формированию математической модели, составим обобщенное дифференциальное уравнение движения динамической модели (для механизма привода утюга), где кинематические характеристики механизма выразим посредством операторов передачи движения. Для этого значения скорости и ускорения звеньев определим через следующие выражения:

Коромысло скорость da _ dp da dt dt dp ’

ускорение	d 2 p   d p d a ( d p Л d 2 a —T = —T--+ | —1 T.                    (20) dt    dt d p V dt J d p
Тяга скорость	d e = d p d p ;                              (21) dt dt d p
ускорение	dp = d p d e , ( dp } 2 d2 в 1 1          1           7.                                                       (221 dt    dt d p  V dt J d p

Цепи утюга и пружины

скорость	ldH - dHnp  d p dH ;                                                   (23) dt      dt    dt d p
ускорение	d2 H ц _ d H пр _ d p dH „ ( d p Y d^H „ 2 =         2=2          +|       1        2 ’                          (24) dt        dt     dt  d p  v dt J d p

Привод скорость	d p = 1 p                         (25) d p    i dt
ускорение	= 1 d p •                              (26) d p     1 dt

При составлении дифференциального уравнения для движения механизма привода утюга используем уравнения Лагранжа второго рода

d ■ dT - dT = Q.,                          (27) dt ddp dp    p где Т – кинетическая энергия системы, выраженная через обобщенную координату;

Q _p - обобщенная сила, соответствующая обобщенной координате.

Кинетическая энергия системы Т состоит из кинетической энергии привода Т_ПР , кулачка Т_КУЛ , коромысла Т_КОР , тяги Т _ТЯГИ , цепи Т_Ц , звездочки Т_ЗВ , утюга Т_У и пружины Т _ПРУЖ .

Т = Т ПР + Т КУЛ + Т КОР + Т ТЯГИ + Т Ц + Т ЗВ + Т У + Т ПРУЖ •                (28)

Кинетическая энергия звеньев, совершающих вращательное движение (приводной механизм, кулачок, коромысло, звездочка), определяется по следующему выражению [3]:

T = 2 J o ,                                    (29)

где J – момент инерции, кгм²;

о - угловая скорость, с ^{- 1} .

В случае плоского движения кинетическая энергия твердого тела (в рассматриваемом механизме таким телом является тяга) находится из следующего соотношения [5]:

T = 2 ( mV ² + J o ²)                           (30)

где m – масса тяги, кг;

J_Z – момент инерции тяги относительно оси, перпендикулярной к плоскости движения и проходящий через центр масс, кгм²;

• V_C – скорость центра масс при поступательном движении тяги, м/с;

• о - угловая скорость вращения, с ^{- 1} .

Как видно из схемы (рис. 3), для скорости центра масс тяги справедливо следующее выражение:

V C = у Д +^S,                             (31)

где V_Д – вектор скорости точки Д ;

Д8 = 0,5 l_T - расстояние от точки Д до центра масс S, м.

Величина вектора скорости точки Д равна

_ d@ d a J

V ^д = lip^К ’

После соответствующего преобразования получим следующее выражение кинетической энергии тяги:

• 1    ,dp^,   da _2l 2, 1, 2, dip.2 da dp                diP^yy

^T T = -(—) ( т т {(—) l r ⁺ -l T ⁺ (   ) ⁺ —l k —l T ^cos( P - ^a ) + J Т (   ) }).          ⁽³³⁾

• 2    dt       d p      4      d p    d p d p                d p

Кинетическая энергия цепи состоит из кинетической энергии цепи, присоединенной к тяге Т _цТ , находящейся на звездочке Т _цЗВ и присоединенной к утюгу Т _цУ .

Рассматривая цепь, присоединенную к тяге, как продолжение тяги, получим следующее выражение кинетической энергии этого участка цепи:

T = 1 ( dp\_{m T}{(—)²l ² + (l_T + -1 _ТУ(^{в 2} + ^цТ 2 ⁽ dt^{7 V цТ {(} dp⁷ к ^{( T} 2 ^цТ ) ⁽ dp⁷

_ da, dp,,    1 _z ч                _T dip. 2,x

+ 2~J lK ~, (Тт + ~1цт )cos(e a) + J цт (~ ) }), dp dp 2                dp где mцЕ

l цТ

= тц -2— - масса цепи, присоединенная к тяге, кг; lц mЦ – масса цепи, кг;

, C +1 cosa ,

• l    _Т = ^к       - l _Т – длина этого участка цепи, м;

ц cos в

J _цТ – момент инерции рассматриваемого участка (определяется относительно оси проходящей через центр масс), кгм².

Кинетическая энергия цепи, находящейся на звездочке, вычисляется по формуле (29), в которой под моментом инерции понимается момент инерции рассматриваемого участка цепи, относительно собственной оси вращения (совпадающей с осью вращения звездочки), а в качестве угловой скорости – угловая скорость звездочки.

Угловая скорость звездочки равна

&;* =    • “- sin( в - a ) .

зв R dt

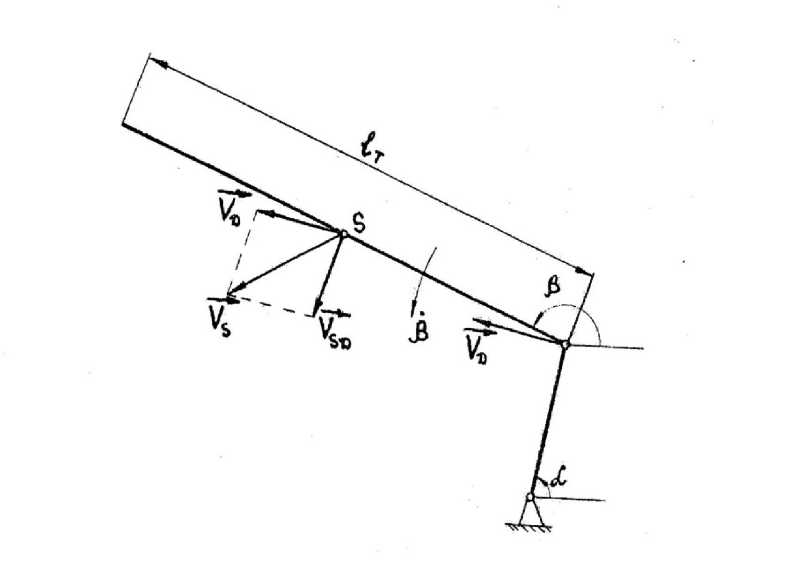
Рис. 3. Схема для определения скорости центра масс тяги

Тогда

Т ц.зв = 1( dh ² J ЗВ ( d a )²{^- sin( в - a )}².                 (35)

• 2    dt       d p    R _3B

Участок цепи, присоединенный к утюгу, движется поступательно. Кинетическая энергия данного участка цепи вычисляется на основе следующего соотношения:

Т у = ¹ m ,y ( dH )².                               (36)

2 dt

H ц где m_цУ = m_ц l_ц

– масса цепи, присоединенная к утюгу, кг.

Подставляя (32)–(34) в (35), получим выражение кинетической энергии цепи

T = (d?)2{m T(dda)2lK2 + (lT +1)2(dl)2 + 2—I'd^X ц                 цТ            к       Тк dt       dp           2   dp     dp

^{X ( l}T + P ) ^X cos ^{( e} - a ^)] + J ЦЗВ ⁽ -l- sin ^{( e} - a ^{)) 2 (} d ^ ^{) 2} + т_Ц у ⁽ d-ц- ^{) 2 }} .

2                    R3e            dp

Кинетическая энергия утюга и пружины вычисляется по формуле (29), в которую подставляются значения массы утюга m_y и пружины (0,33 m_ПРУЖ ) соответственно, а для кинетической энергии системы получим следующее выражение:

1 ,dp_x2(                ^^2 d вР      ^а.2 ,2   1, 2 ,в₂

^T = J J ^{ J пр W2 ⁺ J кул + J кор (т ^{) 2 +} J T ^{(   ] +} т т [⁽— ^{) 2 l} K + — l T (-3 ^{2 +}

2 dt i             dp       dp       dp      4    dp

, da . de ,               ,

+--lv —lT cos(e - a)] + m,lT к Т                     цТ dp  dp

^ d a A ² v d p )

¹ k ⁺1 ^l T + 2 ¹ цт

I d p)

f

цТ

•

•

/ sin (e -a)

I R 3B

( d— A ²

v ^{d p} )

\2

^ d a

) I d p )

d a   d e

+ 2—l К dp  dp

I d p )

•

+ ⁽ J цЗВ + J ЗВ ) •

A ² (

■   ⁺ | ^т цу ^{+ m} у

. 1 A

⁺ 3 ^т пруж )

.

Выражения для вычисления величины момента инерции звеньев механизма привода утюга приведены ниже.

Для вычисления величины обобщенной силы используем принцип возможных перемещений [4, 5], согласно которому придаем системе возможное перемещение 8p >  0.

Получим сумму элементарных работ

( ^5 А ) _p = М 8 А - d p dp - F _T 8 H ,

где М – крутящий момент на валу звездочки, Нм;

dП

— ap - элементарная работа консервативных сил, дж;

d p

F a H - элементарная работа сил трения на направляющих утюга, дж.

Как следует из формулы (39), для обобщенной силы справедливо выражение

Q = M ^ p

—

dП d p

—

dH

F T . d p

Для вычисления обобщенной силы необходимо выразить потенциальную энергию системы в функции обобщенной координаты.

Потенциальная энергия механизма (рис.1) складывается из потенциальной энергии кулачка Пкул , коромысла П , тяги Пт , цепи Пц , утюга Пу и пружины Ппруж , которые определяются из следующих соотношений:

для кулачка

П кул = ^Р кул ( Р цТкул ^Slll ( ^ ⁺ Y 1 ) ^{+ а})

для коромысла

^Пкор = ^Ркор ^{( а + d +} R ^Tkop ^{Sin( a +} Y 2 ) )

для тяги

П Т = Р Т а + d + 1 к ^s i ^{n а} + “ l_T sin в j ;

для цепи

П ц

Р                  1 п

l {1цТ (a + d + A + R3B — — 1цТ Sin в) + ~ R3B [a + d +

+ A + R 3B Sin(-)] + H ц ( a + d + A + — -H ц )};

для утюга

Пу = Ру а + d + A — H

ц

—

для пружины

П пруж

к

h

f

2 J

;

= ¹ ( р  Н + С  ( Н

2 \ пруж¹¹ пруж   ^v пруж V ¹ пруж

—

Н

¹ пруж 0

где Р_кул , Р_кор , Р_Т , Р_ц , Р_у , Р_пруж – силы тяжести кулачка коромысла, тяги, цепи, утюга и пружины, соответственно, Н;

R_цTкул , R_цT к _Op — расстояния от центра масс до оси вращения кулачка и коромысла, соответственно, м;

• а , d , А , h y - геометрические характеристики механизма, выбираемые конструктивно, м;

• Y 1 , y ₂ - угловые характеристики, рад.

Произведя соответствующие преобразования, получим формулу для потенциальной энергии механизма, выраженную через обобщенную координату dn                             ,            dd

= РкулRцTкул c0S(^ + Y1) + РкорRцTкopCOS(a + Y2) — + PT (lk coS a~ + dp                       p p          dp

• 1    d d/L ^Р ц ^dH ц .                1/ 2 о в\

+ —1т ^c0S P -—) + — {—-- ^{( 1} цТ ^{Sin в —} R 3B ^— H ц ) ^— -l ₄ T ^c0S P -—) ^—

• 2    dp 1ц  dp                     2

  _—

  
  

  P_Ц

  
  

  dH_Ц d p

  
  

  + ^{{ C} пр ⁽ H ПР

  
  

  ^H ПР 0 ) ⁺ 2 ^Р ПРУЖ ; ^}

  
  

  dH ПРУЖ d p

  
  

Ввиду того, что ранее рассматривался вопрос о действующих в механизме силах трения, принимаем во внимание только силу трения в направляющих утюга

F t = K ( Р у + С ,р ( Н рж

—

Н J + Р ¹ пруж 0 )   ¹ пруж

—

где Fин   – сила инерции утюга, Н (величина силы инерции определяется по формуле d2 H ц

F = m );

ин у dt²    ’

К – коэффициент, учитывающий направление движения утюга (К = - 0,0747 – при движении вниз, К = 0,089 – при движении вверх).

Подставим выражения кинетической энергии (38), потенциальной энергии, вычисленной через обобщенные координаты (47), и силы трения (48) в уравнение Лагранжа второго рода и при этом осуществим соответствующие преобразования. В результате получим обобщенное уравнение движения механизма привода утюга, выраженное посредством операторов передачи движения.

С =

d2p die a1

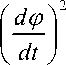
^B i ,

r , 142 T T ,da.2      dda.2,2   1,2 de ,2  da. dp cl = J (-)2+J +J (---Y+mT{(---2 1 + — lT (—^~)2-i

• 1 п                КуЛ кор                *T                     ТК

i             pp        dp 4 dp    вр

• ■ It cos(P — a)} + +(JT + J ЦТ)(dp}2 + m,T {(p )2 /к2 + (^ + к )2(p)2 + dp        dp          2

где

+ 2 dp l„ dP (It +   )cos(P — a)} + +((J,.3, + J_)(p sin(P — a)}2 + dp  dp     2

1       dH 2

^{+ ( т} цу ⁺ m у ⁺ р ПРж ) ⁾⁽— m , K ⁽~— ) ;

3       dp

T ,da d2a , z в 1 = J кор ( , )( ,) + (mT + тЦ dp dp

Pird2 a da , 2 A,, xde d/

—){— 2 —/к + 1 -( l _T + / ц_Т ) +—— } + / _ц   dp² d p     3

1 .                .  da de  da d2в     1   da de dPT  da

+ -/к (/Т + /цТ )cos(P — a ) X---2— +--+ +------x

2 ц            dp dp  dp dp   /Т + /цТ dp dp dp  dp de da. mu d/ dda2.2   1 z, , dPr x tg (в - a )(^--)) + —ц—{(--)2 /K ++ -(/T + /u J2 x (^)2 + кТ цТ dp dp 2p dp dp 3

+ dr1- dr ( /т + /цТ )cos(e — a)} + (m,  ■ + J) X pl2sln2( в — a){d" + dp dp                      /,   R,   dp

+ —ctg(r—a)■ (——da)} + {——(H, dH,+!(H )2} + dp           dp dp     /ц dp     dp2

d ² H dH

+ {mу(1 + K) + -m^, }x-^-рц 6       dp dp с, = M —PRT coAa + yA-P RT cos(a + /J--

1 кул кул цТкул V / 1/ кор цТкор V / 2/ d n         da 1 , d dp.    P, dH,.

• - PT (/к cos a — + -/t cos P —)--—{——(Ц sin в - R3e - H, ) -

• dp 2       dp)    pdp

dHdH

• — - Pt ² cos ^/} + { P     — ( C пр A H пр + - Р пр ) — }(1 + K ).

2        dp      dp2

Выводы

На основе преобразованного уравнения Лагранжа второго рода (в данное уравнение введены выражения: кинетической и потенциальной энергии, вычисленные через обобщенные координаты; силы трения) получено уравнение движения механизма привода утюга, выраженное через операторов передачи движения.