Математическая модель динамики поверхностных вод

1.    Применение модели мелкой воды для описания геофизических течений

Наибольшее развитие получили гидродинамические модели для описания различных физических процессов как в отдельных областях морей и океанов, так и для всего водоема в целом. В рамках таких крупномасштабных моделей изучаются различного рода глобальные циркуляции, изменчивость уровня, динамика солености и ледяных заторов, волновые движения, цунами, аварийные ситуации [8]. Близкими являются задачи определения структуры течений в водохранилищах и равнинных реках для различных прикладных исследований [10].

Выделим успешные попытки построения моделей конкретных водоемов: озеро Ной-зидлер (Австрия), некоторых прибрежных районов северо-западной Атлантики, островов в районе Большого барьерного рифа с использованием неструктурированной сетки, Азовского моря и др [4]. Однако подчеркнем, что задание границы острова на основе неструктурированной сетки сразу теряет эффективность в случае описания затопления суши. При решении задачи динамики поверхностных вод по сухому дну (описание затопления территории) возникают проблемы корректного моделирования границы «вода — сухое дно» [2].

Использование уравнений Сен-Венана не ограничивается описанием только тонкого слоя несжимаемой жидкости на твердой поверхности. С большим успехом модель мелкой воды применяется для изучения динамики вихревых структур в атмосферах планет (например, Юпитера), движения в вязкоэластичной трубке, волновых процессов и ауторегуляции при течении крови в сосудах, аккреционных астрофизических дисков в приближении гидростатического равновесия. Уравнения мелкой воды лежат в основе ряда моделей для расчета адвекции и диффузии загрязняющих веществ на мелководье [3]. В рамках модели мелкой воды рассматриваются многофазные течения и вращающаяся жидкость. Популярными остаются модели динамики тайфунов [9].

Отметим также, что уравнения мелкой воды являются удобной и распространенной моделью для тестирования и апробации численных схем перед рассмотрением системы полных газодинамических уравнений.

2.    Уравнения мелкой воды

Будем исходить из интегральных законов сохранения для однородной несжимаемой жидкости, ограничившись рассмотрением законов сохранения массы и импульса «жидких частиц» с плотностью р = const и объемом V ( t ) , деформирующимся в процессе движения произвольным образом (см. рис. 1):

^ / dV = Q, ut J v (t)

/ udV = - / vf^P)dV + / /dV, ^dt Vv(t)             Jv(t)    ^рР/         Jv(t)

. д . д . d

/ — плотность внешних

где V = е_ж— —+ e_y— —+ ^ez^~; P — изотропное давление;

объемных сил; и = ( и _ж ,и _у ,u _z ) — вектор скорости; Q = Q ( r, t ) — функция источников и стоков жидкости [м ³ / с].

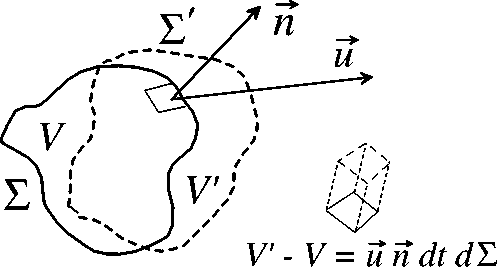
Рис. 1. Превращение объема V (t), ограниченного поверхностью S(t), в объем V(t + dt) = V ‘ c поверхностью S(t + dt) = S ’

Запишем уравнения мелкой воды в интегральной форме, предварительно представив уравнение (1) в виде [11]:

/ dS / dz = 4" / HdS = Q, dt Js)) Jo         dt Js))

где H = H ( x.y.t ) — расстояние от дна z = b ( x,y ) до возмущенной поверхности жидкости p ( x,y,t ) = b ( х,у ) + H ( x,y,t ) (см. рис. 2); S ( t ) — площадь поперечного сечения «жидкой частицы» в плоскости ( х , у ). Аналогично для уравнения (2) при условии гидростатического равновесия в вертикальном направлении р = рд ( р — z ) + р _а и

( u _z ) ₂ = —     u _z dz = 0 ( р _а — атмосферное давление, д = — / _г — ускорение свободного

H Jo падения) имеем:

4 / HUdS = ^dt Js(t)

— g J H V _± pdS +

J HFdS,

_SL + _SL

Эх ^y dy

где ∇ ⊥

U = (Ux,U) = (uD. и F = (Fx,Fy) = (/^)z — средние по z-координате значения скорости и плотности объемных сил в плоскости (х, у) соответ- ственно.

Перейдем к уравнениям мелкой воды в дифференциальной форме. Применяя к уравнениям (3)–(4) правило дифференцирования по времени интегралов от произвольной тензорной функции р = p ( t,x, у )

d [ pdS = /  [^ + Vх (pU)1 dS, dt s(t)             s(t) dt получим уравнения движения мелкой воды в дифференциальной форме (уравнения Сен-

Венана):

ЭН

+V 1(HU)=9.

г7а

• -(-U) + Vх (HU ® U) = —gHVip + H/ ,(6)

dtv / где q = Q/h2 — мощность поверхностных источников [м/с]; h — характерный мелкий горизонтальный масштаб (в численных моделях будем использовать размер ячейки).

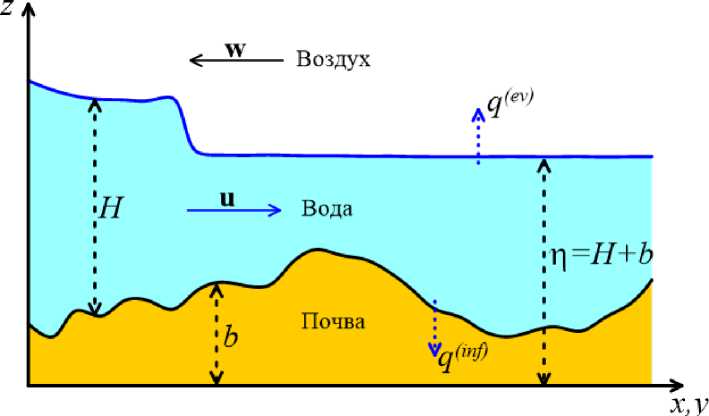
Рис. 2. Характерный пример профиля поверхности суши по данным дистанционного зондирования Земли SRTM 3. ( а ) — Показан срез рельефа земной поверхности в области русла Волги (фрагмент). Особенностью является сильно немонотонный изрезанный (нерегулярный) вид рельефа в случае размера ячейки 50 м. Точки — значения высоты рельефа b в узлах ячеек.

Величины ж и z приведены в метрах

Суммарная плотность сил, действующих на жидкость, в рамках теории мелкой воды представима в виде суперпозиции сил Кориолиса, придонного трения, вязкости и ветра:

F = F _Cor + F _fTTCt + F^ + F (7)

Запишем основные уравнения движения мелкой воды, проецируя их на оси декартовой системы координат:

дН д ( Ни )   д ( Ну)

дt дх ду

д(Ни)    д (   2   1    2А   д(Них)     1 Z)-

+ ах Н + 29оН ) +   ....   = - 2 аН '

- " ^Н _х + f - (9)

^ + '  ■ » ^ + 19Н2) = -1 АНх^- дt       дх ду \2/2

- 9Н|^ + /, (10) ду у где и, у — компоненты вектора скорости v; Н — толщина слоя жидкости; q(x, y,t) — функция источников/стоков; 9 = 9.8 м/с2; у = Н + b — уровень свободной поверхности воды; f(Cor') = —2QZу и f,((Cor') = 2^zи — компоненты силы Кориолиса; ^z — вертикальная компонента угловой скорости вращения Земли на соответствующей широте, величина гидравлического трения

А = 29п ^ /Н ^4/3                               (11)

зависит от коэффициента трения по Маннингу п м .

3.    Источники и стоки воды

В уравнении (8) функция источника / стоков определяется следующим образом:

q = q^^s^ - q^$ ) - q^,

где q ^(s) — приток за счет источников; q^^m! ) — инфильтрация; q ^(ey) — испарение.

Потери воды с единицы поверхности q ^{( - )} = q ^(e) + q^^m! ) определяются скоростями испарения q ^(e) и инфильтрации q^^m! ) . Величина q ^(e) в общем случае сложно зависит от температурного и ветрового режимов, влажности воздуха, конвективного состояния атмосферы.

Для баланса интенсивностей источников и стоков воды можно записать:

q ( ^,y,^ = ^s + q ° = ^S + q^ -

- q ' ) ( ж, у, h, I g , Н д , Т д , T _w ) - q ^(e) ( h, a, 3, T _w , T _a ) , (13)

где учитываются факторы, определяющие баланс источников и стоков воды [7].

3.1.    Источники

q (^s) = q ^(s) ( ж, у, t ) — скорость притока воды [м/с].

| ^(s) ( t ) = J f q ^{( s}^( x,y,t ) dxdy — суммарный расход источника (м ³ / с), где S k — площадь источника.

В случае регулируемого стока через плотины задается величина суммарного расхода (гидрограф), а скорость притока воды определяется по формуле

q ^(s) ( t ) = | ^(s) ( t ) /S _fc

Когда источником воды являются осадки, то скорость притока воды определяется интенсивностью осадков на заданной территории.

3.2.    Однослойные степенные модели инфильтрации, зависящие только от глубины воды H

Рассмотрим нелинейную модель инфильтрации воды в почву (рис. 3), которая более адекватно моделирует процесс впитывания воды по сравнению с cr ^(m!) = const . В большинстве математических моделей, используемых при моделировании динамики поверхностных вод, применяются модели линейной или экспоненциальной фильтрации. Однако экспериментальные данные свидетельствуют о более сложном механизме впитывания (см. рис. 4). Наиболее адекватной моделью фильтрации является нелинейная модель с насыщением. В предлагаемой модели величина сг ^(т!) , входящая в уравнение (13), определяется следующим образом:

q6-4 ) = _o<*«f ) ₍₁ - „ ) ^Н, Н *

da _ а^11) а dt = ^НЙТ — ^7, здесь ст*гп/) — скорость впитывания воды толщиной слоя Н в сухую почву; а = V^/V — коэффициент влагонасыщенности почвы; Vw — объем воды, содержащейся в почвенном покрове с объемом VI; ^ — пористость почвы; т1 — характерное время осушения почвы за счет испарения и инфильтрации воды в подпочвенный слой с малой пористостью (глина)[5].

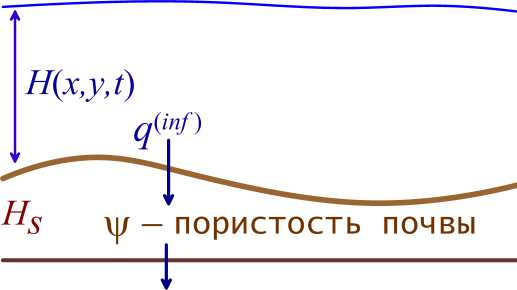
Рис. 3. Схема нелинейной модели инфильтрации

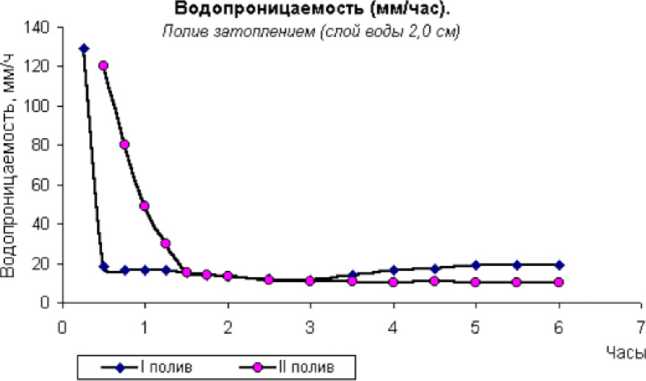
Рис. 4. Характерные профили скорости впитывания в грунт по экспериментальным данным

4.    Основные силы4.1.    Сила гидравлического трения между жидкостью и дном

В математической модели учитывается гидравлическое сопротивление:

• •    прямого равномерного русла;

• •    нерегулярной структуры дна;

• •    извилистости русла;

• •    различных препятствий;

• •    растительности;

• турбулентности;

• •    иных физических факторов.

Обсудим влияние коэффициента шероховатости дна по Маннингу п _м в модели (9)–(10), учитывающей эффективное трение между водой и дном, на динамику воды в реках. Часто используемая формула Маннинга для средней скорости потока вдоль русла реки [12]

U =

R 2/3 I ^1/2 п м

зависит от средних вдоль русла реки значений уклона дна I и гидравлического радиуса R _g = В/P ( В и Р — средние вдоль русла реки значения площади поперечного сечения и периметра смачивания соответственно). Для широкой реки имеем R _g = Н ср ( Н ср — среднее значение глубины вдоль русла реки). В случае Волги ниже Волжской плотины для оценок примем R _g ~ 5 м, I ~ 5 • 10 ^-5 , U ~ 1 м/с. При экспериментальном определении гидравлического сопротивления русла рассчитываются коэффициенты Шези:

с = и/^1Нф,

I — средний вдоль русла реки уклон водной поверхности. Использование (16) дает для коэффициента шероховатости Волги п _м ~ 0 . 02 .

Перечислим физические факторы, влияющие на гидравлическое сопротивление потоку воды в речном русле, которое принято характеризовать параметром п _м :

П м = П о + П 1 + П 2 + П 3 + П 4 + П 5 + П б ,

где учитывается гидравлическое сопротивление прямого равномерного русла п ₀ , нерегулярной структуры дна п 1 , извилистости русла п ₂ , различных препятствий п ₃ , растительности п ₄ , турбулентности п ₅ и иных физических факторов п ₆ .

Каждый из перечисленных факторов может давать свой вклад в увеличение параметра п _м для выбранной модели гидравлического сопротивления, причем действие указанных механизмов является взаимосвязанным. Коэффициент шероховатости при использовании формулы Маннинга (16) или ее аналогов имеет проблемы с физическим смыслом, поэтому к величине п _м при рассмотрении речных русел следует относиться как к эмпирическому параметру, эффективно учитывающему большую совокупность факторов.

Укажем на опубликованные оценки параметра шероховатости для некоторых русел. Величина пм для различных больших рек лежит в широких пределах, как правило, различаясь на разных участках реки. Например, для р. Ангара пм = 0.021-0.031 (дер. Татарка), р. Лена пм = 0.023-0.054 (пос. Змеиново), р. Витим пм = 0.016-0.060 (г. Бодайбо), р. Енисей пм = 0.017-0.039 (Подкаменная Тунгуска), р. Подкаменная Тунгуска пм = 0.022-0.035 (пос. Черный остров). Результаты моделирования гидрологического режима Чебоксарского водохранилища дали для коэффициента шероховатости значения 0.022–0.026. Калибровка по данным 17-ти гидропостов в дельте Волги и 3-м постам на Нижней Волге в 1977-1978 гг. дала для коэффициента Шези С = 40-66 м1/2/с, что для Нср = 5 м по формуле Маннинга пм = Нс1р/6/С дает пм ^ 0.02-0.033. В качестве примера из зарубежных речных систем стоит отметить оценки коэффициента шероховатости рек Янцзы, Хуанхэ, Миссисипи, Рейна, который находился в пределах пм = 0.01-0.2 [6].

4.2.    Сила внутреннего вязкого трения у DISC = _^Т

Т — тензор вязких

Т

1 XX

напряжений в модели мелкой воды.

= 2 ,/^ ,Т„ = 2 „Н^ ,_Т = „,н ( ⁹^ + ^д^ ) . ^t дх' ""  ^t ду ^{Xy t (} ах ' ду )

Коэффициент турбулентной вязкости v _t рассчитывается по формуле:

, t = с^. I (^ ) 2 +( а^ ^ ) 2 +1( дт ^х + а? ) 2 , у дх ду 2 дх ду

С ~ 0 . 04 — эмпирическая постоянная; h² — площадь расчетной ячейки.

4.3.    Влияние ветра

Аэродинамическое сопротивление водной поверхности можно описать следующим образом:

^d = ^С« Р « ( - - - ) • | ^ - - | .                         (22)

^H p w

Состояние водной поверхности С _а :

С _а = (0 . 5 + 0 . 1 | w | ) • 10 ^-3 .                                 (23)

Заключение

Уравнения Сен-Венана позволяют учитывать большое количество различных факторов, среди которых можно выделить неоднородный рельеф дна, метеорологические условия и трение между потоком и дном. Были построены модели, описывающие: 1) характер инфильтрации/испарения воды; 2) изменения коэффициента шероховатости в зависимости от уровня воды в водотоке.