Математическая модель динамики работы запертого объема шесеренного насоса с учетом движения подпятника

ствует до сих пор. Это происходит вследствие сложности процессов протекающих в запертом объеме. Многие исследователи создавали свои модели [1, 2, 3, 5, 6, 7] для исследования аналогичных систем, однако до сих пор нет общепринятого четкого понимания всех процессов, протекающих при работе шестеренного насоса. Стоит отметить, что для тихоходных насосов существуют, доказавшие свою эффективность, четкие рекомендации по разработке мероприятия для увеличения ресурса за счет разгрузки запертого объема, которые, однако, не пригодны для быстроходных насосов. Для них в условиях производства чаще всего подбирают конфигурацию разгрузочных канавок опытным путем, проводя огромное количество опытов.

В данной же работе для определения эффективных мероприятий использовалась, созданная авторами математическая модель. Эффективность предлагаемых мероприятий оценивалась по размаху импульса давления в запертом объеме. Для того чтобы определить давление в запертом объеме необходимо было определить его величину запертого объема и площади контакта запертого объема с областями нагнетания и всасывания через разгрузочные канавки. Значения площадей контакта разгрузочных канавок определялись численно.

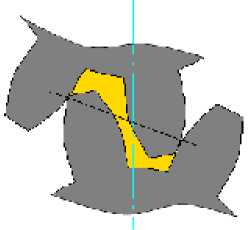
Рис. 1. Схема образования запертого объема

Стоит отметить, что на динамику работы влияли не только разгрузочные канавки, но и передвижения подпятников из за повышения давления в запертом объеме.

Численно была найдена функция запертого объема от угла поворота шестерни (рис. 2). Здесь и далее все зависимости от угла поворота шестерни представлены в диапазоне от 0 (что соответствует моменту образования запертого объема) до 8,5 градусов (что соответствует моменту раскрытия запертого объема).

Давление в запертом объеме можно найти из следующей системы уравнений [3]:

Q 30 = Q . + Q h + Q b ;

dVП

^QСЖ     , ;

dt

<

Q_H = ± p F„ Н НН

Qr = ± p FB

B BB

K

^{2 A} P h

² A P b

1 dV_n

----

•

VП dp

;

;

где, Q_ЗО – геометрический расход запертого объема; p – давление в запертом объеме; Q_H – расход в область нагнетания; Q _B – расход в область всасывания; V_П – приведенный запертый объем; p H , p B - коэффициенты расхода площадей контакта запертого объема с областями нагнетания и всасывания соответственно; F_H , F_B – площадь контакта запертого объема с полостями нагнетания и всасывания соответственно; A p H , A p_B - разность между давлением в запертом объеме и давлением нагнетания и всасыва-

ния соответственно; р - плотность рабочей жидкости; K – объемный модуль упругости.

В модели приняты следующие допущения: коэффициенты расхода в область нагнетания p _H и в область всасывания p B из запертого объема приняты постоянными.

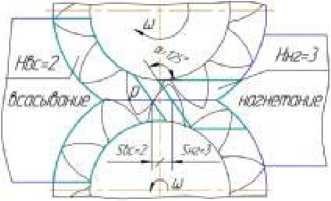
В представленной модели есть возможность конфигурирования разгрузочных канавок путем изменения следующих пяти параметров (рис. 3):

а - угол наклона перемычки; 5* НГ - смещение перемычки в сторону области нагнетания; S_ВС - смещение перемычки в сторону области всасывания; H_НГ - глубина разгрузочной канавки в области нагнетания; H_ВС - глубина разгрузочной канавки в области всасывания.

На основе предложенной модели, стало возможно подобрать конфигурацию разгрузочных канавок, обеспечивающую требуемое давление в запертом объеме.

Стоит также отметить, что изменение запертого объема приводит к передвижению подпятника. Схема к расчету перемещения подпятника показана на рис. 4. Из основных уравнений динамики можно определить ускорение подвижного подпятника. Таким образом, в любой момент времени ускорение подпятника может быть определено из следующего выражения:

dx V m l- = p П - Cx, dt2 6 ’ где m – масса подпятника; x – перемещение подпятника; С – жесткость системы.

Скорость подпятника вычислялась следующим образом:

dxi dt

dx    d ² x

-г^{1 +}      "^А t , пРи ⁰ <  x < ^xmax ;

dt dt

-

k

dx i - i

dt ’

при

х, = 0;

. х i = х Mi AX •

где A t - дискретизация по времени; x_MAX - мак-

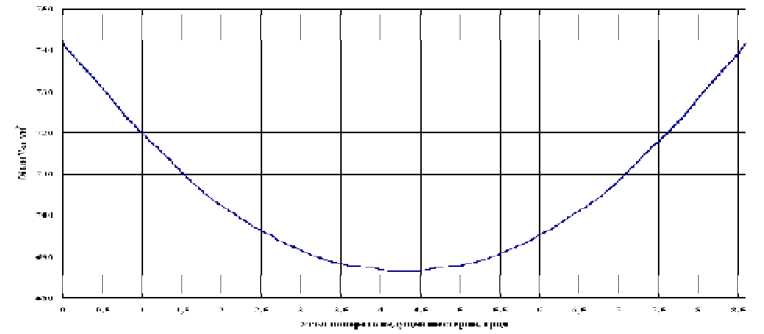
Рис. 2. Гра фик изменения объема запертого объема в зависимости от углового положени я шестерен

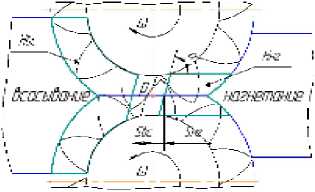
Рис. 3. Параметры, определяющие геометрию разгрузочных канавок симально допустимое системой перемещение подпятника; k – коэффициент потерь при соударении.

Перемещение подпятника определятся следующим образом:

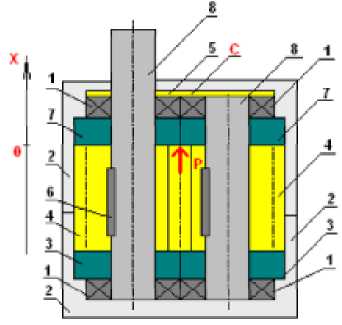
Рис. 4. Расчетная схема для определения смещения подпятника:

1– подшипники; 2 – корпус; 3 – неподвижные подпятники; 4 – зубчатые шестерни; 5 – упругий элемент(прокладка); 6 – шпонка; 7– подвижный подпятник; 8 – валы

„           d ² x      dx. A t ² „

0, при х - - +    . A t + i ■    <  0

dt ²       dt 2

dt ²

dx - 1

x i =^ x i - 1 +— ii ¹ A t +

¹i - 1

dt

d ² x i - 1 dt ²

A t ²      „       . dx      d ² x A t ²

■~, при 0 <  x _H + —- ^A +—T^- •— < x _MAx,

2                 dt      dt ²    2

dx     d ² x A t ²

xMAX, пРи 0 < xi-1 + -,7 At + -.T-    ■ dt dt   2

Согласно [6], образование такого зазора влечет к появлению торцевых утечек. В процессе работы действительные торцовые зазоры являются переменными. Изменения величины зазоров вызываются биением торцов шестерен, пульсацией давления в нагнетательном трубопроводе, отклонениями от плоскостности сопряженных торцов роторов и уплотняющих деталей, неровностями на торцовых поверхностях деталей, компрессией жидкости во впадинах зубьев и упругой деформацией поверхностей скольжения в зоне контактирования. Поэтому расчетная зависимость для потерь через торцовые зазоры должна включать их величины в качестве переменных функций. При всех возможных изменениях торцового зазора его минимальная величина не должна быть меньше значений, гарантирующих сохранение масляной пленки между трущимися поверхностями. Это одно из основных требований, предъявляемых к конструкции шестеренных насосов любой разновидности. В расчетах использовалась следующая формула для определения величины утечек через торцевые неплотности:

_nT_,       x x¹ в н - P b )

Q y = ( p H p B )

12^^ ln— , r1

где в _н и P _B - углы соответствующие полости нагнетания и всасывания; r ₁ и r ₂ – радиусы внутренней и внешней границы торцевого зазора.

На основе предложенной модели была проанализирована эффективность применения большого ряда вариантов разгрузочных канавок, подобрана конфигурация, обеспечивающая максимальное снижение импульсов давления в запертом объеме. Геометрия исходного и предложенного профиля разгрузочной канавки представлены на рисунках 5а и 5б. На рис. 6 и 7 показаны пульсации давления в запертом объеме на одном и том же режиме при исходном и предложенном профиле.

По полученным функциям давления от угла поворота шестерни были определены перемещения подпятника. Эти зависимости показаны на рис. 8 и 9.

По зависимостям смещения подпятника от угла поворота шестерни (рис. 8 и 9), а также с учетом постоянной составляющей зазора (для этого насоса 10 мкм), были получены импульсы расхода через торцевые неплотности. Они представлены на рис. 10 и 11.

Разработанная математическая модель позволила выполнить канавки, обеспечивающие снижением амплитуды пульсаций давления в запертом объеме в три раза. В настоящее время как за рубежом [1, 2], так и у нас ведуться разработки активних и адаптивних систем по снижению виброакустической нагруженности ше-стеренних насосов, хотя стоит отметить, что пока ни одна такая система не внедрена в серийное производство.

Еще одним важным результатом модели является получение зависимости торцевых утечек от угла поворота ведущей шестерни. В работе было показано, что порядок торцевых утечек зависит от эффективности работ разгрузочных канавок. Стоит отметить, что большинство специалистов полагают, что торцевые утечки являются преобладающими в шестеренных насосах, а в их уменьшении есть некий запас по увеличению КПД.

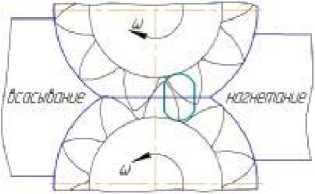
а)

б)

Рис. 5. Исходный (а) и предлагаемый (б) профиль разгрузочных канавок

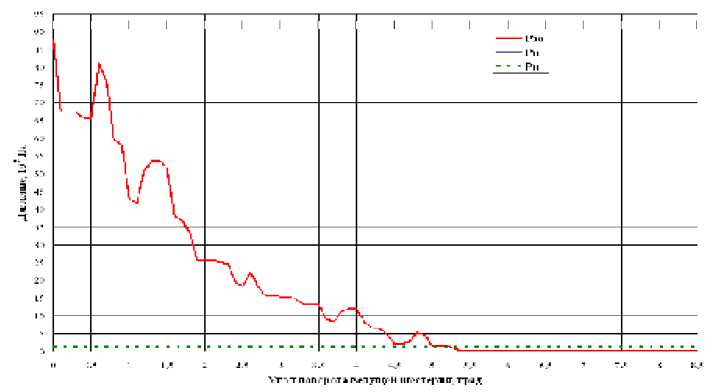
Рис. 6. Рассчитанное давление в запертом объеме при исходном профиле

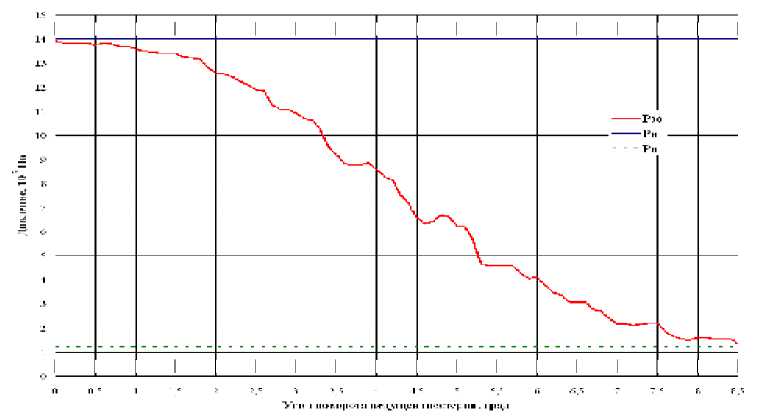
Рис. 7. Рассчитанное давление в запертом объеме при предложенном профиле

В настоящее время за рубежом [8] активно осваивают методы определения пульсаций утечек по пульсациям давления для последующей диагностики состояния качающего узла. Для этого сперва определяют пульсационную производительность качающего узла в лабораторных условиях, затем в рабочей системе, зная пульсационную производительность качающего узла и пульсации давления на выходе из насоса, определяют импеданс системы. В процессе работы, зная импеданс и измеряя пульсации давления, вычисляют пульсационную производительность. По изменению пульсаций потока определяют пульсации утечек диагностируют состояние насоса. Однако стоит отметить, что импеданс системы после определенного времени работы будет меняться, к тому же пульсации потока, определенные в лабораторных условиях могут отличаться от пульсационной производительность в системе, таким образом этот метод диагностики насосов вряд ли имеет перспективы вследствие, вероятно, малой точности.

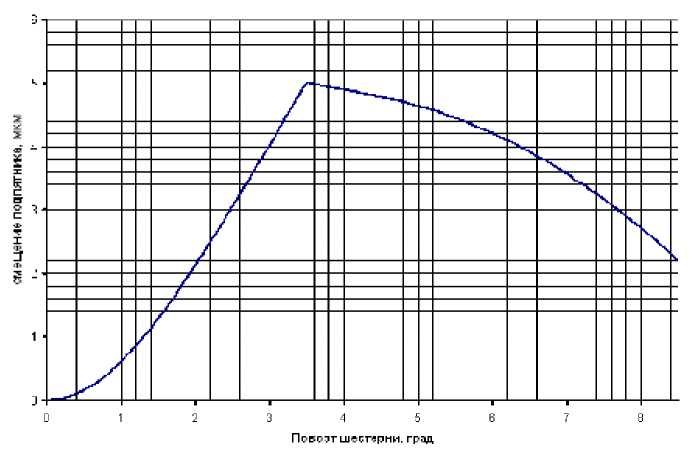
Рис. 8. Смещение подпятника при исходном профиле разгрузочных канавок

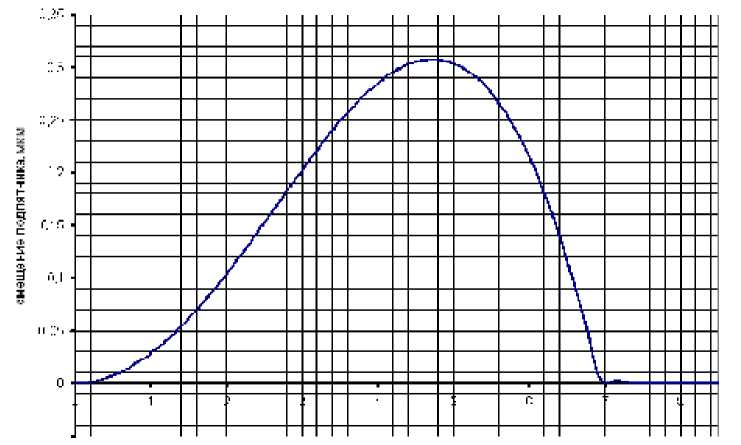
Поверг шестерни. m-'Д

Рис. 9. Смещение подпятника при предложенном профиле разгрузочных канавок

Несмотря на то, что этот метод малопригоден для диагностики износа всего насоса с помощью него можно диагностировать насколько эффективно работают разгрузочные канавки и насколько изношены пары трения шестерня подпятник. Современные насосы позволяют снижать радиальные утечки и утечки через неплотности контакта зубьев практически до нуля. Торцевые же утечки составляют основную долю утечек насоса. Если считать импеданс насоса не зависящем от конфигурации разгрузочных канавок, то описанным выше методом можно определять изменение утечек через торцевой зазор. Этот метод будет не точен, зато он даст порядок числа, а как было показано выше эффективное снижение заброса давления в запертом объеме в несколько раз дает изменение пульсационных торцевых утечек на несколько порядков. Таким образом по изменению утечек можно судить об эффективности работы разгрузочных канавок и об износе пары трения шестерня подпятник.