Математическая модель для исследования свойств магистралей транспортных сетей при использовании нескольких классов обслуживания

Математическая модель для расчета показателей качества обслуживания МСС при использовании нескольких классов обслуживания

Современные МСС обычно используют несколько классов обслуживания, при этом для каждого класса может использоваться как свой план распределения информации (ПРИ), так и свои отдельные очереди в телекоммуникационных устройствах [1-2]. В общем случае маршрутные таблицы (МТ) для пакетов различных классов могут быть различными, поэтому сама МТ будет не двумерной, а трехмерной, а в качестве третьего индекса элементов МТ m ^U4u‘v^s) будет выступать номер очереди.

Обозначим через М. МТ i-узла, учитывающую особенности передачи трафика для каждого se[l,S] класса обслуживания и имеющую раз- мер гл(п„-1)х8 . Тогда ПРИ для сети в целом может быть записан в виде:

M = {M,,..,M,.,..,M,J.

Рассмотрим приведенный на рис. 1 фрагмент узла. При передаче пакетов по сети с несколькими классами обслуживания необходимо определить не только исходящее из узла направление, по которому следует направить пакет дальше по сети, но и выходную очередь направления, соответствующую приоритету или классу обслуживания пакета. Пусть каждая выходная очередь обслуживается логическим каналом с пропускной способностью С_у$ ’ тогда трехмерный массив ^ 1-^5 К xn xS будет содержать пропускные способности ветвей сети, выделяемые для передачи каждого класса трафика.

Введем следующие обозначения:

• - обозначим через ^  t^^/5 К„ХИ XS матри

цу интенсивностей поступления потоков. Тогда элемент ^" kls будет равен потоку s класса, который необходимо передать по сети между рассматриваемой парой узлов к и /;

• - через И [1? ••> H_s ’ ••’ Ms ] вектор размерности S, ц – элемент которого равен обратной величине среднего размера длины пакета в битах для трафика класса s ;

  - через T_y задержку при передаче пакета по ветви Qu3 , s – очередь, через Яу – вероятность ее блокировки, через °ij_S^и ®ijs – очередь и число мест ожидания, через ^ijs – поток, поступающий на ветвь (У) В 5 очередь системы буфер-канал, через P "" уровень ее загрузки. Эти величины будем хранить в трехмерных массивах:

^ — [^" ijs ]^Mx^x5 ’ ^ — L^" zjslnMxnMxS ’ o = [Oys]wxS, w = [Wy,]wxS,

^ ^-^ ijs -l«_w x«_M xS ’ P ^-P ijs ^n_u xn_u xS *

Обозначим через о = l<5_kls ]_vvS ,

V^kls KwxnuxS ’ ^   1-^/5 КцХ^х^ ’ ^ ^kZslnMxnMxS матрицы размером n„xnMxS , содержащие информацию о характеристиках качества обслуживания между каждой парой узлов для каждого класса обслуживания.

Матрица о будет содержать вероятности потерь пакетов, матрица T – возникающие при этом задержки, матрица X – число переприемов (хопов), матрица z – вероятности зацикливания пакетов.

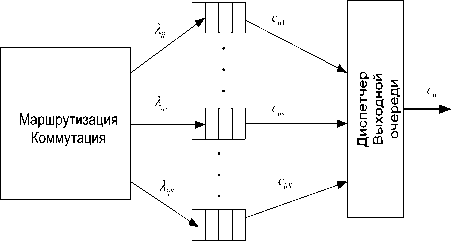
Рис. 1. Демультиплексирование выходного потока в соответствии с классом обслуживания

Поскольку на сетях с использованием нескольких классов обслуживания элементы МТ i -узла зависят от класса обслуживаемого, то для каждого класса обслуживания необходимо рассчитывать свою матрицу переходных вероятностей (МПВ), которая, как и в случае с одним классом обслуживания, будет квадратной.

Не изменится также вид матриц и векторов, являющихся результатом ее обработки.

Обозначим через pU) МПВ, соответствующую s – классу обслуживания, а через N – фундаментальную матрицу, тогда будет справедливо следующее:

P⁽ⁿ ={Pj\..,Pj\..,P^};

_N⁽o =^Nj\..,Nj\..,Nj^ ■

Для удобства будем хранить результаты вычислений соответствующих матриц и векторов в трехмерных массивах:

¹⁷ L/^ijs J(^_/+1)x(_Mm+1)x5’

N (Z) = Г/7(/)1

^ L^ijs J(^,+l)x(^+l)x5-

С учетом ранее введенных обозначений для случая с классами обслуживания для элементов МПВ может быть записано:

P(,) =/р(Мл); Nw =4(P(Z)),V/e[l,n„],V5e[l,S]

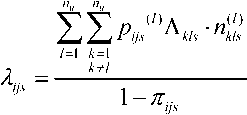
Запишем последнее выражение с учетом введенных в этом пункте обозначений:

Х = Л(ЛЛ,л).

Таким образом, для случая с S классами обслуживания с учетом введенных в этом пункте обозначений аналогичная система будет выглядеть следующим образом:

X ~ Xg ,

р(,)=4(м,л),     v/e[i^],v^O],n(/) = Zv(p('A       v/e[i^],v^O],

■ X = Л (P(,), N(Z), Л, л), V/ е Й, V» e O], л = Л(Х),

c = £cs.

,        1=1

Если записать эту систему в виде отдельных уравнений, то она будет содержать переменные типа \s ’ ^ijs ’ ⁿkis ’ Pijs . Количество уравнений каждого типа и переменные, входящие в эти уравнения, приведены в таблице 1.

Из этой таблицы видно, что число приведенных уравнений системы совпадает с числом неизвестных и равно З^рДи.,-^-!-!- . Это означает, что выполняется одно из необходимых условий существования единственного решения системы.

Таблица 1. Число различных типов переменных в системе

Тип уравнения	Число уравнений	Число переменных типа
					rij.S
Р(,)=//М,л)		-	St		S-nu.u-Xf
N(,)=/V(P('))		-	-
X = /z,(P,',,N",,A,n)	S • г	St	St	s -i)2
Я = 4(X)	S-r	St	S -r

Исследование влияния изменения нагрузки и пропускных способностей каналов

Современные мультисервисные сети характеризуются значительными колебаниями нагрузки в течение достаточно коротких промежутков времени. Используя описанную выше модель, проанализируем влияние изменения величины поступающей нагрузки при неизменном характере тяготения для случаев, когда пропускная способность каналов, соединяющих соседние узлы, составляет соответственно С = 1 Гбит/С и С = 2 Мбит/С. Топология сети приведена на рис. 2, а результаты расчетов показаны на рис. 3 [3]. При расчетах приняты следующие исходные данные:

• -    топология – кольцевая;

• -    число узлов – 8;

• -    характер тяготения – централизованный;

• -    число центров тяготения – 1, номер ЦМУ – 1;

• -    число классов обслуживания – 4;

• -    тип СМО, описывающей СБК – M/D/1/N;

• -    варианты расчета:

• -    вариант 1а: пропускная способность каналов на каждом участке С = 1 Гбит/С;

• -    вариант 1б: пропускная способность каналов на каждом участке С = 2 Мбит/С;

• -    варианты 2а и 2б: отличаются от вариантов 1а и 1б тем, что пропускная способность ветвей (1-2) и (1-8) удвоена;

• -    нагрузка на сеть – меняющаяся. А ’ А ’ А ’ А – интенсивности поступления пакетов соответственно 1, 2, 3 и 4 классов примем равными Л которая изменяется в диапазоне Я = 0-7,5-10³ пак/С при С = 1 Гбит/С и Л = 0 —1,5-10¹ пак/с при С = 2 Мбит/С. (Заметим, что диапазон изменения нагрузки выбран таким образом, чтобы уровни загрузки ветвей для С = 1 Гбит/С и С = 2 Мбит/С совпадали);

• -    размеры пакетов 1-4 классов:

1рак\ = 500 [бит], 1рак2 = 1000[бг//и],

1ракЗ = 5000[6ww], IpakA = 15000[бши];

• -    доля пропускной способности каналов сети, отводимая для передачи пакетов 1-4 классов: С ₄ = 0,5 С ; С ₃ = 0,3 С ; С ₂ = 0,1 С ; С ₁ = 0,1 С ;

• -    размер буферной памяти для каждого класса обслуживания (У = 10[иотс].

Результаты расчета:

• -    ^sr₄ ^ ^sr₃ ’ ^sr₂ ^? ^5Г| ^Х^) – зависимости среднесетевых задержек от интенсивности поступления пакетов для каждого из 4 классов до и после удвоения пропускных способностей ветвей (1-8) и (1-2);

• ^-    ^^V^sr^s, = № – зависимости среднесетевых потерь от интенсивности поступления пакетов для каждого из 4 классов обслуживания до и после удвоения пропускных способностей ветвей (1-8) и (1-2);

• -    Psr₄ ’ Psr₃ •> Psr. ’ Psr_x - /(^) – зависимости среднесетевых уровней загрузок каналов от интенсивности поступления пакетов для каждого из 4 классов обслуживания до и после удвоения пропускных способностей ветвей (1-8) и (1-2).

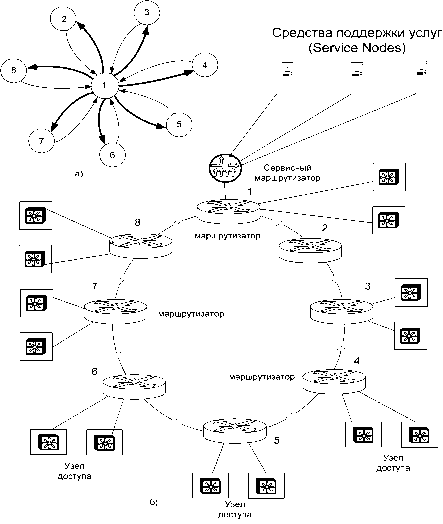
Рис.2. Пример построения магистрали транспортной сети с кольцевой топологией: а) – структура тяготения; б) – топология сети.

Соответствующие графики приведены на рис. 3. Цифрами в кружочках на графиках отмечены номера вариантов расчета. Цифра «1» соответствует случаю, когда пропускные способности всех каналов сети равны между собой. Цифрой «2» помечены графики, когда пропускные способности наиболее перегруженных ветвей (1-8) и (1-2) удвоены. Заметим, что некоторые оси на графиках имеют по две шкалы. Значения на первой проставлены обычным шрифтом и соответствуют С = 1 Гбит/С. Значения на второй выделены жирным шрифтом и соответствуют С = 2 Мбит/С. Нетрудно видеть, что среднесетевые характеристики существенно зависят от класса обслуживания. При этом наименьшие задержки и потери соответствуют первому классу обслуживания, а наибольшие – четвертому классу.