Математическая модель для исследования устойчивости двухосного автомобиля с индивидуальным приводом при разгоне на прямолинейном участке

В настоящее время появились конструкции различных систем распределения мощности, которые позволяют регулировать крутящие моменты на каждом ведущем колесе в соответствии с условиями движения, независимо от условий движения других колес. Такие конструкции создали базу, благодаря которой стал возможен дальнейший качественно новый этап в развитии теории и разработке более совершенных оптимальных схем привода.

Новый этап может быть сформулирован как создание управления эксплуатационными свойствами путем разработки систем распределения мощности с задаваемыми управляемыми характеристиками. Развить данное направление теории простым суммированием результатов исследований, уже выполненных отдельными авторами, невозможно в силу следующих причин:

• -    положения существующей теории ориентированы на использование традиционных для крупносерийного машиностроения технических решений: постоянно включенный дифференциальный или подключаемый блокированный привод, использование дифференциальных механизмов, часто имеющих различную схему блокировки и т. д.;

• -    исследования по отдельным разделам теории мобильных колесных машин носят причинно-следственный характер. Это означает, что в методологическом плане такие исследования относятся к работам анализа, поскольку содержащиеся в них рекомендации по выбору характеристик и параметров машин получены путем сопоставительного анализа.

Одним из важнейших вопросов при разработке новой конструкции системы распределения мощности является обоснование правильного распределения моментов, которое можно охарактеризовать коэффициентом распределения крутящих моментов к_м. Не трудно убедиться, что большее значение к_м обеспечивает повышение тяговых качеств автомобиля за счет рационального использования сцепного веса ведущего моста. А это, в свою очередь, обеспечивает лучшую динамичность и проходимость автомобиля в условиях различных сил сцепления ведущих колес с дорожной поверхностью. Однако значительная величина к_м может оказать отрицательное воздействие на устойчивость, управляемость и топливную экономичность автомобиля.

Следовательно, степень распределения моментов нужно ограничивать, исходя из условий, при которых указанное отрицательное воздействие минимально или отсутствует.

Очевидно, что влияние степени распределения моментов на поведение автомобиля наиболее существенно при движении на повороте, а также при прямолинейном движении в случае трогания с места и разгоне, или движении автомобиля на подъем в условиях, когда силы сцепления ведущих колес с поверхностью различны.

Чтобы получить рациональный характер распределения крутящих моментов между колесами двухосного автомобиля, на основе уравнений Лагранжа второго рода были составлены дифференциальные уравнениями движения материальной системы (рис. 1) по трем степеням свободы X Z Д ■

■ jx' = Е^2 +^^Х1 COS^j "^Ry sin^ , т • jy -mH(b-bH)P = ^ R'y2 +^ Ry\ cos 0t - ^ Rxisin ^ > (1)

Марченко С.Н., Келлер А.В.,           Математическая модель для исследования устойчивости

Драгунов ГД.двухосного автомобиля с индивидуальным приводом ...

Jj = (R"_x2 -R"_x2)0,5B₂₊(R'_x1 -^)0,5Д cos^ -^R^b-

-^Ryacosex-^R^asine^

где т - полная масса автомобиля; щ„ - масса неподрессоренных частей; J_z - момент ин ерции автомобиля вокруг вертикальной оси, проходящей через центр масс О'; R¹^ - сила тяги на колесах автомобиля; К'_И - боковые реакции на колесах автомобиля; Bj - ширина колеи соответствующего моста; SMau - суммарный стабилизирующий момент на колесах; а, Ъ - координаты центра масс в продольном направлении; Ь„ - расстояние центра неподрессоренных масс до задней оси; 6 - среднее значение угла поворота управляемых колес.

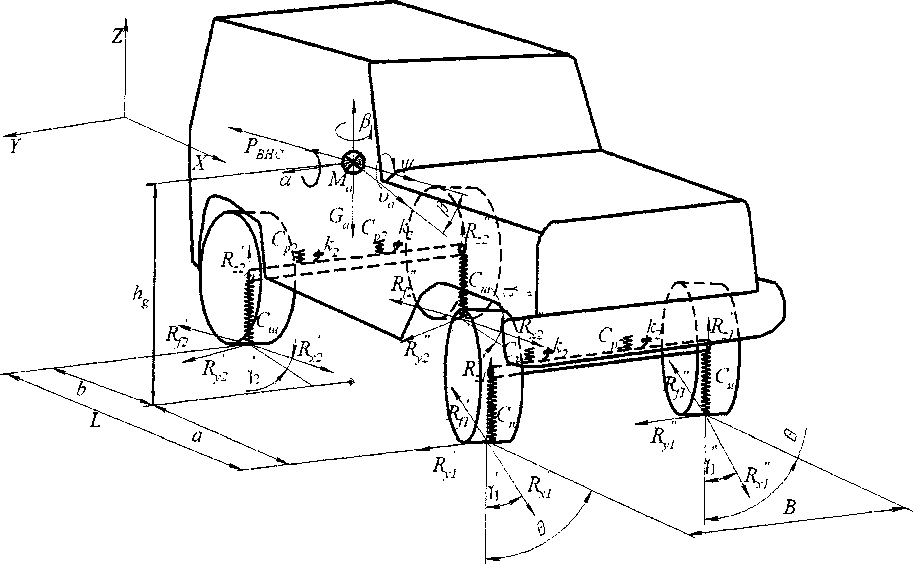
Рис. 1. Расчетная схема автомобиля

Ускорения центра масс по соответствующим осям определяют из кинематических соотношений:

h = йХ’ - ОуР, jy = Оу - ихф,                       ■ где Oj - скорость центра масс по соответствующей координате; /3' - производная по углу разворота автомобиля.

Для определения величин действующих вертикальных реакций R_zj в месте контакта колес с дорогой составим основные уравнения движения центра подрессоренных масс по двум степеням свободы а, ^. Пренебрегая в этих уравнениях членами второго порядка, получим:

^J™ + 2f^r_P\4 + ^T_Pi^bk >« + ²ГC_xa²_k + C₂b; )а + М^ + M_nj_x, (h_k-r_k) = 0,

^пкх "*" ^nbkp ~*~ ^чД ~^ б^-чу — О^^ )\\! — Jnkzx^ — M^j^jу + Мр — О, где JnKy - момент инерции подрессоренных масс относительно поперечной оси, проходящей через центр масс Ок; М„ - подрессоренная масса автомобиля; гр- коэффициент сопротивления амортизатора; hKp - плечо крена кузова; М\- момент сухого трения в подвеске в продольном направлении; JnKI - момент инерции подрессоренных масс относительно продольной оси, проходящей через центр масс Ок; JnK2X - центробежный момент инерции подрессоренных масс; rk - радиус колеса; ак, bK, hK - координаты центра тяжести подрессоренных масс; Су- приведенная жесткость рессоры в вертикальном направлении; С^ - приведенная жесткость подвески в поперечном направлении; 1ц - приведенный коэффициент демпфирования в поперечном направлении

Расчет и конструирование

k_v⁼^’^l^rpj^pi ’ ^f - момент сухого трения подвески в поперечном направлении d

В случае пробоя передней подвески дифференциальное уравнение движения (2) по координате а запишется в виде:

Л^^й + 2^₂^^й + 2CC_tolaj + С₂Ь_к)а-2а_к(С_шХ -С^ + ^Р'р^ + M_nj_x\h_k -r_k) = 0,     (3)

где / 'i - ход передней части кузова до пробоя рессоры по оси передних колес; Сю - вертикальная жесткость тины переднего колеса.

Уравнения (2) и (3) позволяют определить усилия, передаваемые через элементы подвески автомобиля на подрессоренные части. Учитывая, что угловые колебания кузова записаны от положения статического равновесия, определим вертикальные составляющие на колесах автомобиля в процессе разгона:

RV-R^ + 0,5R“±^, где R‘Zjcm - величина статической нагрузки на колесе; Ra2j - динамическая нагрузка, передаваемая через рессору при дифференте кузова; ZlR^q -динамическая нагрузка, передаваемая через рессору при крене кузова.

После этого получим:

R“y = 2а_к (С^а + г , при а < —.

Р“1=2ак[Сю1а-(С1й1-С1Л1,при а>К ак           ак

^“2 - 2^ (С2а + гр2а), m^r'.-r^

С^ + К_уф + M_Fj sign^

Траектория движения автомобиля во время разгона определяется наличием углов увода переднего и заднего мостов, которые возникают под действием боковых сил R!_yj, приложенных в пятне контакта колес с дорогой. Используя кинематические соотношения, определим величины боковых реакций на каждом колесе автомобиля для малых углов:

R_yi-^7^+^ -t_g^---),

. ob-Vv

Ry2 -kgy’ziY^ tg , где 6^ - угол разворота колес управляемого моста вследствие крена кузова; к5 - значение коэффициента сопротивления увода колеса при оптимальной нагрузке; ^zj, ^q - корректирующие коэффициенты. -

В зависимости от величины силы тяги и нагрузки на колесе коэффициент сопротивления боковому уводу изменяется по известному закону [Л]. Значения корректирующих коэффициентов в расчетах определяли по следующим зависимостям:

^=2,4

п

^zjojo J

-1,8

D

^zjojo J

+ 0,4

п zjojo ?

, Гх# =

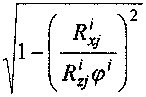
где Rqonm - оптимальная нагрузка на колесо; ф - коэффициент сцепления под колесами соответствующего борта автомобиля.

Для определения законов изменения основных силовых факторов, действующих на автомобиль в процессе разгона с индивидуальным приводом ведущих колес, найдем основные парамет-

Марченко С.Н., Келлер А.В., Драгунов Г.Д.

ры траектории движения центра масс, которые получим при решении системы дифференциальных уравнений (1). Для удобства систему приведем к виду со = А ; их. = Б - Цу со ; и у = В - их.ю,

J,        J, 2J          2JJ

m

YR' +yR\cos0_l-YR\ sin#

^ _ b^ -v2  ^^ vl      1   ^^ XlJ , мдъ-ъл .

Д =---—co^p.

M

Тогда координаты траектории движения центра масс автомобиля можно определить как t                     tt

Р = ^codt; х = J^- cosP - uy, sinp^dt; у = J(ty cosp + Цу sinP^dt, 0             00

где x, у - координаты центра масс механической системы на плоскости; 3 - угол разворота продольной оси.

В процессе разгона рост сил тяги R_xj (рис. 2) на ведущих колесах сопровождается дифферентом кузова а и увеличением вертикальных нагрузок на колеса задней оси.

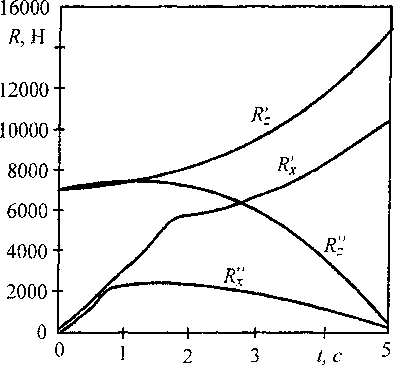
Рис. 2. Изменение параметров автомобиля при разгоне

Вследствие различных сил тяги на ведущих колесах в горизонтальной плоскости возникает поворачивающий момент, который обусловливает появление боковых реакций на колесах и углов увода, а кроме того, приводит к развороту передних управляемых колес за счет податливости деталей рулевого привода, что способствует появлению дополнительного угла разворота управляемых колес вру, который в данном случае выступает как дестабилизирующий фактор.

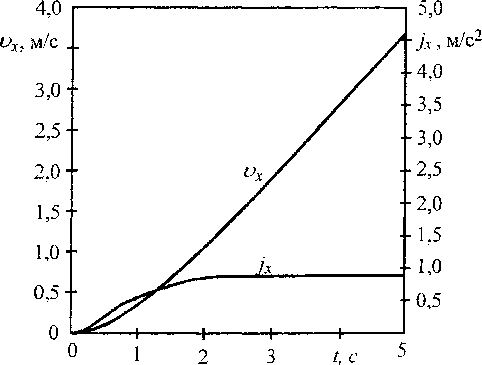
Отмеченные выше явления приводят к началу движения автомобиля по криволинейной траектории (рис. 3). Движение по криволинейной траектории сопровождается действием на подрессоренные массы поперечной силы инерции за счет возникновения бокового ускорения j_v. Это приводит к крену кузова ^ и соответствующему перераспределению вертикальной нагрузки R',, (см. рис. 2) в сторону колес с большими действующими силами тяги, что в свою очередь при работе системы управления приведет к еще большему увеличению на них сил тяги. Следовательно, при наличии неравномерности коэффициентов сцепления ведущих колес имеем возмущенный характер движения автомобиля. При этом в процессе разгона автомобиля возможно достижение предельной силы сцепления на колесах переднего моста, что может привести к потере ими способности воспринимать боковые усилия без скольжения и потери вследствие этого управляемости. Начавшееся регулирование крутящих моментов на ведущих колесах уже в переходной ста-

Расчет и конструирование

дии может обеспечить автомобилю требуемый уровень управляемости при высокой динамике разгона.

Снижение величины начальной неравномерности сил тяги на ведущих колесах способствует уменьшению отклонений центра масс от направления движения. Однако при больших значениях неравномерности коэффициентов сцепления ведущих колес выравнивание характеристик процесса заканчивается при некотором положительном угле /3 разворота продольной оси, под которым впоследствии автомобиль продолжает движение. В случае отсутствия корректирующего воздействия со стороны водителя в данной ситуации возможен выход автомобиля из своего ряда движения.

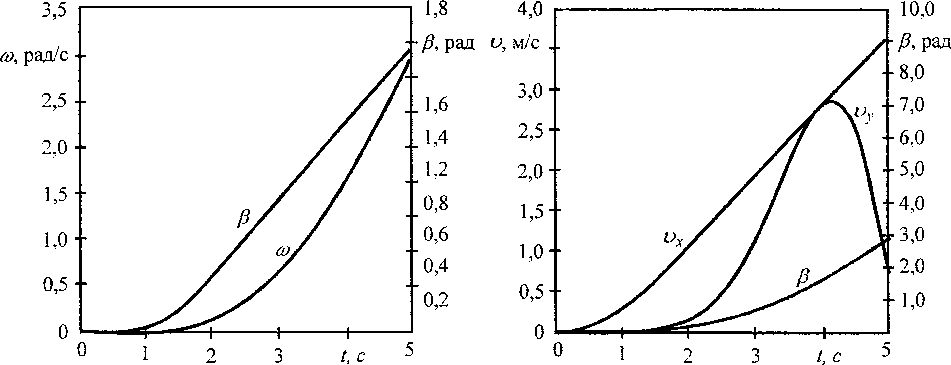
Рис. 3. Изменение параметров, характеризующих траекторию автомобиля при разгоне

Чтобы определить крайние точки автомобиля при теоретическом анализе, воспользуемся координатой смещения центра масс в боковом направлении у и углом разворота продольной оси /3. С учетом габаритных размеров запишем отклонения крайних точек для передней и задней частей кузова:

ух = у + аг sin Р + 0,55г cos р sign /3, у^= y-b2smp - 0,5Вг cos р sign р, где аг, Ьг - расстояние от центра масс соответственно до передней и задней части кузова; Вг - ширина кузова автомобиля.

Тогда значение коэффициента устойчивости определим из отношения разности величин допускаемой полуширины полосы дороги (назовем ее шириной коридора безопасности) и максимального отклонения крайних точек кузова автомобиля в процессе разгона от осевой линии к разности этих же величин в исходном положении при нахождении центра масс на осевой линии полосы:

0,55_d -|yj п, =------— ,

0,5(Sd-SJ где Вд - ширина коридора безопасности.

При этом потеря устойчивости наблюдается при т;г<0, причем степень неустойчивости характеризуют отрицательные величины коэффициента??Л

Таким образом, разработанная математическая модель позволяет определить рациональный характер распределения крутящего момента по ведущим колесам и оценить его влияние на устойчивость движения автомобиля.