Математическая модель для магнитооптической структуры ускорительного кольца в накопителе заряженных частиц

Ускорительные установки используются во многих областях современной науки и техники. Они применяются для нужд медицины, обработки материалов, промышленных производств, но прежде всего ускорители находят применение в фундаментальной науке.

В настоящее время перспективным проектом для научных исследований является строящийся коллайдер NICA , который создается на базе Объединенного института ядерных исследований в России, на территории города Дубна.

Мегапроект NICA – коллайдер протонов и тяжёлых ионов, цель которого – изучение свойств плотной барионной материи [1]. После запуска коллайдера NICA учёные ОИЯИ смогут воссоздать в лабораторных условиях особое состояние вещества, в котором пребывала наша Вселенная первые мгновения после Большого Взрыва, – кварк-глюонную плазму (КГП) [1].

Основой адронных и ионных коллайдеров являются накопители заряженных частиц (накопительные кольца). Это установки, обеспечивающие накопление заряженных частиц на стационарных орбитах [2].

Проведение эксперимента в физике элементарных частиц начинается с этапа моделирования. На этом этапе оцениваются необходимые параметры эксперимента: характер начального распределения пучка, количество исследуемых частиц, характеристики необходимых магнитооптических (далее по тексту – оптические) элементов накопительного кольца.

При моделировании динамики пучка заряженных частиц может применяться как подход, основанный на приближенных вычислениях, так и аналитический подход. В первом случае используются численные методы (метод Рунге-Кутта, метод Эйлера, интерполяция сплайнами и т.д.). Все эти методы предполагают заданную точность вычислений и будут накапливать ошибку при непосредственном моделировании. Вопрос минимизации ошибки принципиально важен для долговременной динамики пучков частиц, при которой объём экспериментальных данных увеличивается экспоненциально. Аналитический подход основывается на линейном вычислении динамики пучка с заданным шагом интегрирования без использования приближенных методов. Использование линейных вычислений позволит приблизить результаты моделирования к экспериментальным данным.

Математическая модель

Формализовать динамику движения пучка заряженных частиц в аналитическом подходе можно с помощью использования линейной алгебры. Кольцо ускорителя, в котором происходит вращение пучка, представляется в виде последовательности матриц. Оптические элементы ускорителя, необходимые для фокусирования траектории частиц, представляются в виде матриц с определенными величинами, а пучок заряженных частиц – в виде последовательности векторов. Каждый вектор имеет следующие величины (см. форм. 1) [3].

'x'

x y. y

^$ (a p )

Переменные x и x’ отвечают за горизонтальную динамику частицы, y и y’ за вертикальную, s и Δp за продольную.

Кольцо ускорителя представляется в виде матриц с определенными элементами. Задача моделирования динамики пучка сводится к перемножению матриц оптических элементов кольца на векторы координат частиц в различных динамиках [3].

Общий вид матрицы оптического элемента представлен ниже (см. форм. 2) .

f 1	A t	0	0	0	0 "		f x 1
a x	1	0	0	0	0		x
0	0	1	b y	0	0	х	y '	(2)
0	0	c y	1	0	0		y
0	0	0	0	1	dz		s
( 0	0	0	0	f z	1 )		A p)

В зависимости от того, какие элементы матрицы являются ненулевыми, траектория частицы меняется на заданные коэффициенты в определенных динамиках. Частица может двигаться в любой комбинации из трех динамик: вертикальной, горизонтальной и продольной [3].

Запишем результаты умножений в горизонтальной динамике, опираясь на заданный общий вид матрицы (см. форм. 2, 3, 4) .

х=1*х + х'*Д( х' = ах * х + l * х'

В данном примере следующие величины являются ненулевыми: a x , At , b y , C y , d z , f z . К горизонтальной динамике относятся: a x , At , к вертикальной: b y , c y и к продольной: d z , f z . Оставшиеся элементы матрицы нулевые и не влияют на изменение траектории частицы.

Используя полученные математические выводы, может быть получена следующая итерационная формула (см. форм. 5) .

x		f 1    A t   0   0   0   0"		f x 1
x		a 10000 x		x '
y	=	001 b 00	х	y	(5)
y		0   0    cy   1    0   0		y
s		00001 d		s
(A p)	i	0   0   0   0    f   1 z		A p )	i - 1

Каждый i -ый вектор координат частицы двигается по j -ой матрице кольца ускорителя. После перемножения вектора на матрицу координаты частицы меняются на соответствующие коэффициенты в определенных динамиках [3].

Оптическая структура ионного накопителя

Проект ускорительного комплекса содержит эталонную орбиту. Эталонная орбита - это идеальная орбита, по которой должны двигаться заряженные частицы. Для успешного эксперимента необходимо изменять траекторию частиц и циклически фокусировать пучок таким образом, чтобы его отклонение от эталонной орбиты не превышало установленного предельного значения . Изменение траектории и фокусировка становятся возможными благодаря внедрению электромагнитных полей, формирующихся с помощью специальных оптических элементов. Согласно вышесказанному, оптические элементы формализуются в виде математических моделей, имеющих вид матриц с определенными величинами. Рассмотрим далее конкретные варианты этих матриц.

Оптические элементы, которые направляют и фокусируют пучок заряженных частиц, могут быть изображены схематично следующим образом (см. рис. 1) .

Изгибающий элемент

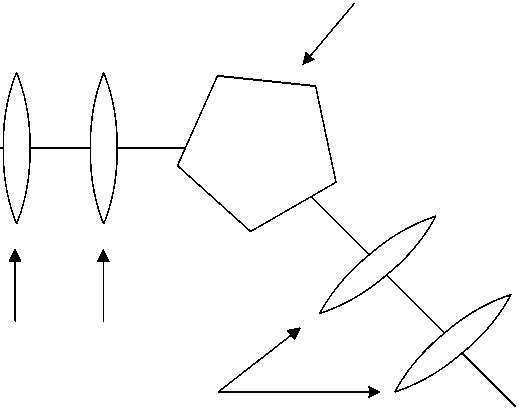
Фокусирующие элементы

Рис. 1. Типы оптических элементов

Структура ускорительного кольца

Ускорительное кольцо ионного накопителя представляет собой набор фокусирующих и дефокусирующих оптических элементов. Элементы располагаются таким образом, чтобы сохранять траекторию пучка частиц на эталонной орбите. В простейшем варианте кольцо может быть устроено следующим образом:

• -    фокусирующая квадрупольная линза;

• -    дрейфовое пространство;

• -    дипольный магнит;

• -    дрейфовое пространство;

• -    дефокусирующая квадрупольная линза.

Цикличность повторения данной структуры зависит от физических параметров реального ускорительного комплекса. Собственно фокусировка пучка заряженных частиц достигается повторением структуры, обязательно включающей комбинацию дефокусирующей и фокусирующей линз. Рассмотрим каждый элемент структуры подробно.

Дрейфовое пространство

Дрейфовое пространство характеризует область оптической структуры, не имеющей электромагнитного поля, соответственно, на этой области не выполняется фокусировка пучка заряженных частиц. Каждый элемент дрейфового пространства имеет длину L.

Транспортная матрица для дрейфовой камеры выглядит следующим образом (см. форм. 6) [4].

( 1 L 0  0

0     0   ^

R =

1 L

0 L

( 0  0  0  0

о 2  2

P s Y s

¹    )

Элементы транспортной матрицы вычисляются по преобразованиям Лоренца (см. форм. 7, 8) [5].

P s = ^

где v - скорость, с - скорость света в вакууме.

Y = ,-------

J1^

Дипольный магнит

Дипольный магнит - это оптический элемент, который используется для формирования траектории движения пучка заряженных частиц. Диполь, имеющий длину L , с однородным электромагнитным полем B отклоняет частицу в горизонтальной динамике на определенный угол 6 , согласно радиусу расчетной орбиты р (см. рис. 2) [6].

Угол 6 можно рассчитать:

если 6 пренебрежительно мало:

sin(2) =

L

2р

_ 1LB

= 2Вр;

-©4

то можно привести к следующему виду:

LB ^в ~(Вр)'

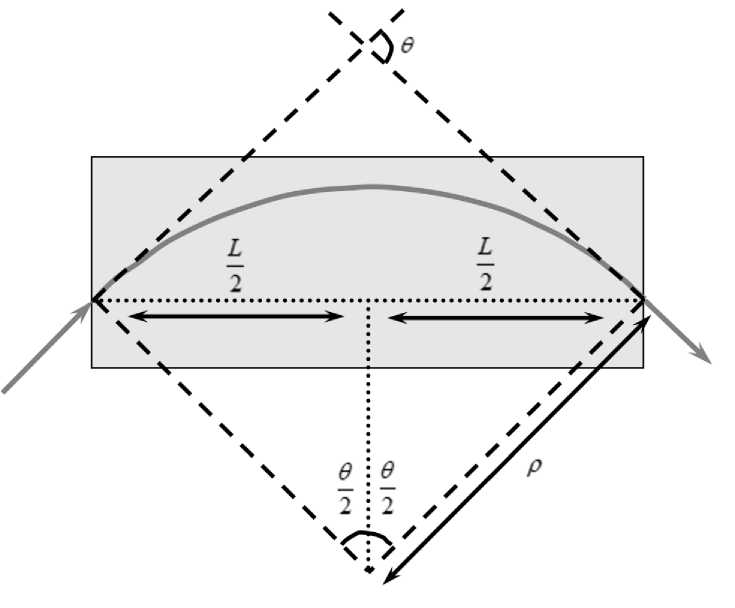
Рис. 2. Схема дипольного магнита

Дипольный магнит характеризуется углом магнита ANGLE , задаваемым квадрупольным коэффициентом K 1 , углом поворота для входного полюса E 1 , углом поворота для выходного полюса E 2 , интегралом поля FINT , величиной половины зазора магнита HGAP , углом поворота вокруг продольной оси

TILT, секступольным коэффициентом K2, величиной изгиба входного полюса Hi и величиной изгиба выходного полюса H2.

Транспортная матрица дипольного магнита представлена на формуле (12) [4].

	c x	s x	0
	- k 2 S x	c x	0
R =	0	0	c y
	0	0	- k ysy
	- _h_ ess	- —d P s d	0
	V 0	0	0

	h   ,      ^
00	e d x
	h
00	Js x
s y 0	0	(12)
c y 0	0
	L 2
01	--i 2  2      2 J 1 P , Y , P ,
00	1           )

Элементы транспортной матрицы вычисляются согласно формулам (7) , (8) , (13) , (14) , (15) , (16) , (17) , (18) , (19) , (20) , (21) [4].

ANGLE * =   L kx — V^2 + K ky = V-K i	(13) (14) (15)
cx — cos (kx x L) sin (kx x L) S^ k x (1 - cos(kx x L)) ^ -             22 kx L — Sv J 1 —  k^ kx Gy — cos (ky x L) sin (kv x L) S y —     2 ky	(16) (17) (18) (19) (20) (21)

Квадрупольная линза

Квадрупольная линза - это оптический элемент, который фокусирует частицы в вертикальной динамике на эталонную траекторию. Квадруполь имеет два северных магнитных полюса и два южных. Полюса симметрично расположены вокруг центра, а магнитное поле вдоль центральной оси отсутствует. На рис. 3 представлена квадрупольная линза, которая фокусирует пучок в горизонтальной динамике и дефокусирует пучок в вертикальной динамике [6].

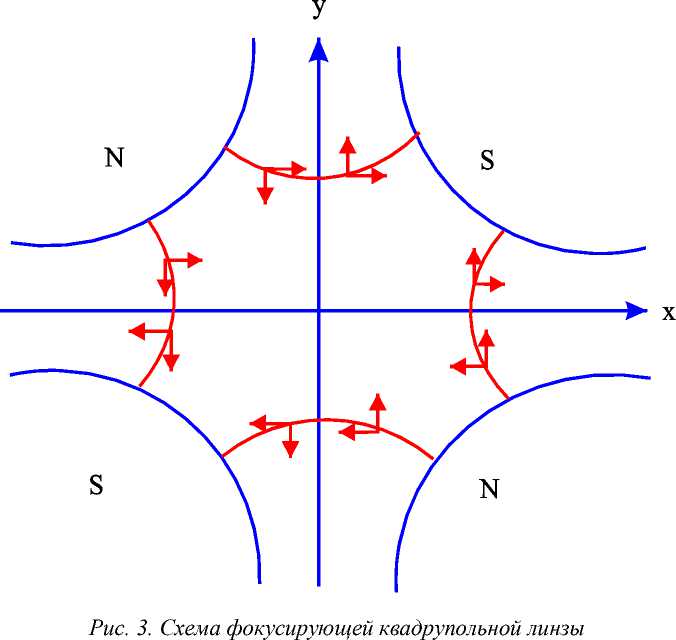
Транспортная матрица для квадрупольной линзы представлена на формуле (22) [4].

	c x - k x S x	s x c x	0 0	0 0	0 0	0   1 0
	0	0	c y	s y	0	0
F =	0	0	- k ysy	c y	0	0
	0 .    0	0 0	0 0	0 0	1 0	L
						22 P.Y s 1      J

Элементы матрицы вычисляются по формулам: (7) , (8) , (14) , (15) , (16) , (17) , (20) и (21) .

Заключение

Выполнена формализация циклической структуры накопителя заряженных частиц. Определена математическая модель ускорительного кольца, в рамках которой введена итерационная формула вычисления динамики пучка частиц. Для основных оптических элементов ускорительного кольца составлены их транспортные матрицы.

В дальнейших исследованиях планируется реализация программного алгоритма моделирования динамики пучка заряженных частиц, позволяющего снизить ошибку вычисления динамики пучка частиц за счёт использования линейных алгебраических операций.