Математическая модель движения продуктов взрыва в шпуре для обеспечения процесса направленного разрушения горных пород

При взрыве удлиненного цилиндрического заряда в шпуре происходят быстропротекающие сложные газодинамические процессы, зависящие от типа ВВ, конструкций зарядов, способов инициирования, кинетики взрывчатого превращения, и дальнейшее истечение газообразных продуктов взрыва в атмосферу. Процесс трещинообразования горной породы в плоскости раскола между смежными шпурами представляет собой обеспечение динамического воздействия взрывной нагрузи на массив. Математический расчет определения динамических нагрузок в зарядной полости сводится к рассмотрению соответствующей газодинамической задачи о распределении газообразных продуктов взрыва (давлений, скоростей) и исходя из этого импульса взрыва вдоль внутренней поверхности шпура.

При этом необходимо рассмотреть две механические задачи: о движении газообразных продуктов взрыва в зарядной полости и о движении массива горной породы под воздействием взрыва (под движением подразумеваются массовые движения среды). Для обоснования требуется сопоставить скорости движения различных сред – газообразных продуктов взрыва и массового движения частиц горной породы. Необходимо рассмотреть совместное движение двух сред (продуктов взрыва ВВ и массовое движение ГП), которое определяет процесс развития магистральной трещины между смежными зарядами.

Разделение процесса на фазы является условным и производится в соответствии с наличием граничных условий в механическом процессе взрыва удлиненного заряда.

В теории газодинамических процессов в шпуре процесс, вызванный распространением детонационной волны по длине заряда, описывается как одномерное нестационарное движение ПВ. Правомерность такой постановки базируется на оценках, непосредственно вытекающих из исходных условий: диаметра полости много меньше его длины; большей сжимаемости породы, чем продуктов взрыва; скорости газодинамических возмущений в них намного больше скорости звука в воздухе. Известно, что скальные горные породы имеют большую акустическую жесткость и незначительное расширение камуфлетной полости. В этом случае выравнивание распределений параметров ПВ по сечению шпура происходит за время, сопоставимое со временем взрывчатого перемещения ВВ по всей длине колонки заряда. Как следствие, при рассмотрении процесса «в целом», т.е. в масштабе длины зарядной полости, временем выравнивания давления по сечению можно пренебречь и считать это выравнивание мгновенным.

Основные функции состояния и движения ПВ зависят от пространственной (осевой) координаты Z и времени t. Газ считается идеальным. Состояние газа по длине шпура (скважины) описывается системой уравнений газовой динамики, базирующихся на учете основных законов механики (сохранения массы, импульса, энергии) в форме, соответствующей одномерной модели нестационарного течения. После детонации ВВ идет процесс взрывного горения и они занимают объем, равный при мгновенной детонации объему, ранее занимаемому зарядом. Полагаем, что ПВ вступают в работу по генерированию квазистатического поля напряжений в процессе расширения взрывной камеры до конечных размеров. Нестационарное истечение обусловлено распадом начального разрыва (1-го рода) между этими параметрами ПВ и параметрами невозмущенного воздуха.

Образующееся при этом течение автомодельно, то есть развивается подобно самому себе единообразно во времени, движение продуктов взрыва сопровождается возникновением ударной волны, формирующейся в процессе движения газов по длине зарядной камеры. Значения параметров массовой скорости, давления и плотности на фронте ударной волны определяются по формулам:

U 1

P 1

P 0

к + 1

2 • к

• ^ s l ¹

• I M ²

M ²

к -1

к + 1 V       2 • к

Р 1 _ ( ^{к +} 1 ) - M ²

^р 0    ^{2 +} ( ^{к -} 1 )

где U — - скорость ударной волны, распространяющейся по невозмущенному газу; Р о , Р о -

U соответственно давление и плотность невозмущенного газа; к - показатель адиабаты для газа; M = ——

– число Маха, a ₀ – скорость звука в воздухе.

P

Соотношение, определяющее число Маха для ударной волны, возникшей при распаде разрыва ^m

P 0

записывается в виде:

P m

P 0

^f 2 ^к - M ² - ^к )

v ^к о ^{+ 1       к} о ^{+ 1}Л

^к 0 ^{+ 1}

X            \

1 1 M • a 0 ]

M ² )    ^a 1   )

2 к 1

^к 1 ^{- 1}

где P m - давление ПВ после расширения до сечения скважины; а 1 - местная скорость звука в ПВ; к 1 -показатель адиабаты ПВ [1].

Возникшее течение по длине зарядной камеры содержит ударную волну, контактную поверхность и волну разрежения. В дальнейшем, с истечением продуктов взрыва из устья шпура, процесс меняется, поэтому область применимости данного решения ограничивается.

Численная оценка эффекта квазистатического давления ПВ сделана на примере взрыва шпурового заряда с глубиной Н = 3 м и при длине заряда равной 2/3 глубины шпура. При линейной скорости детонации ДШ 6,5 ^ 10 3 м/с и скорости движения газообразных продуктов в шпуре 0.7 ^ 10 3 м/с давление в средней части удлиненного заряда составляет 2000·10^-6 с.

Необходимо сопоставить полученные значения давления с оценками длительности воздействия взрыва в средней части колонки заряда при расстоянии между шпурами 0.5 м. Этот участок волна напряжений покрывает примерно за 50·10^-6с, то есть за время в 35-40 раз меньше, чем время установившегося давления в рассматриваемом сечении шпура. В этом случае можно считать, что в области массива между зарядными полостями устанавливается квазистатическое поле напряжений. Также известно, что скорость распространения трещин в горных породах составляет (0.2÷0.4) с р скорости продольной волны. Следовательно, для данного случая в скальных породах процесс трещинообразования между смежными зарядными полостями осуществляется за 125·10^-6 с, то есть он происходит за время существенно большее, чем время действия волны напряжений, и значительно меньшее, чем время действия установившегося квазистатического давления продуктов взрыва.

На рис. 1 показана эпюра распределения давления ПВ по длине шпура в различные моменты времени. Таким образом, на основе выполненных расчетов можно утверждать, что процесс направленного разрушения происходит за счет квазистатического действия давления ПВ.

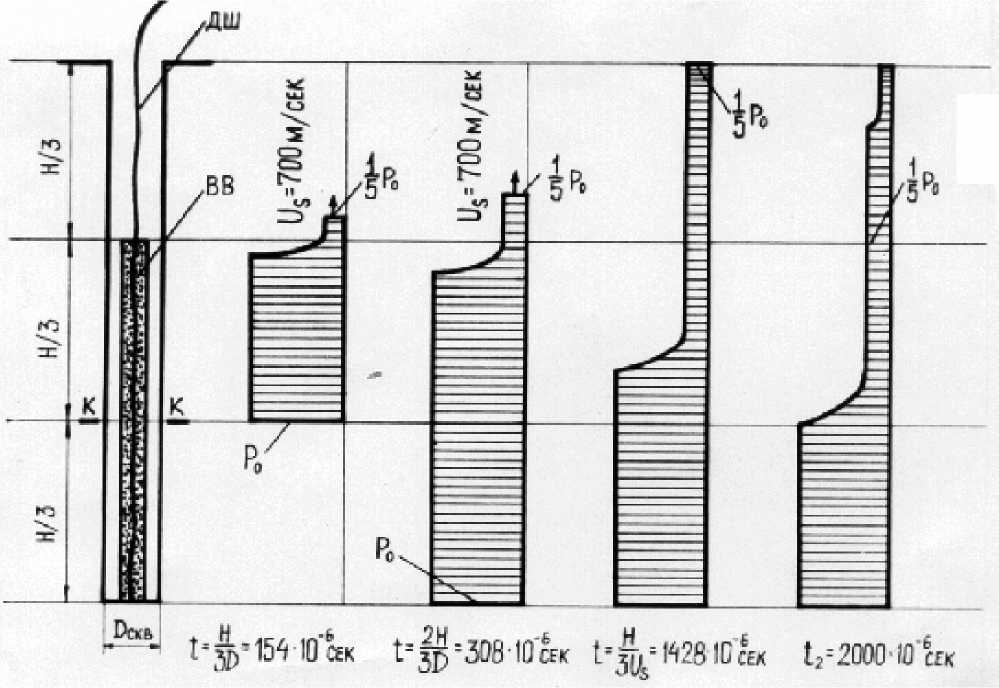
Рис. 1 Распределение давления ПВ в шпуре

Для получения более полной картины распространения волны напряжений и процесса развития магистральной трещины за счет интерференции волн напряжений были проведены модельные экспериментальные исследования методом скоростной фотосъемки. Кинограмма процесса распространения волн напряжений и развития трещинообразования представлена на рис. 2 (а,б,в,г) с интервалом 18 мкс.

Как видно из рис. 2, продукты детонации радиально расширяются и трансформируются в материал модели в виде волны напряжений с коническим фронтом по длине зарядной полости. Распространение волны напряжений вызывает местные смещения частиц материала, которые создают напряженное состояние среды, и в оптически активных материалах появляются темные линии (изохромы), распространяющиеся со скоростью продольных волн в среде.

При взаимодействии волн напряжений происходит развитие магистральной трещины между удлиненными цилиндрическими полостями, что приводит к увеличению скорости роста магистральной трещины, величина которой составляет (0.3–0.4) cр, где ср – скорость продольной волны в оптическом стекле. При дальнейшем движении этой плоскости происходит слияние в единую плоскость трещинообразования. На основании наглядной картины распространения волн напряжений в процессе трещинообразования можно представить разрушение твердой среды следующим образом. Вблизи заряда растягивающие напряжения превышают предел прочности на растяжение, поэтому образуются системы радиальных трещин, а смятия образующейся части взрывной полости не происходит, т.к. давление продуктов взрыва меньше, чем предел прочности на сжатие.

При взаимодействии волн увеличивается растягивающее напряжение по линии расположения взрывных полостей, в результате чего образуется магистральная трещина. Этот процесс можно рассматривать как квазистатический, в котором расположение напряжений определяет развитие трещины.

Ступенчатая поверхность плоскости раскола модели из оптического стекла свидетельствует, что процесс прорастания трещины носит скачкообразный характер. Это объясняется пульсирующим характером движения трещины за счет промежуточных релаксационных процессов напряжений на ее вершинах. Пульсация обусловлена тем, что величина интенсивности напряжений в вершине трещины, необходимая для дальнейшего роста и определяется временем подпитки необходимого уровня интенсивности напряжений.

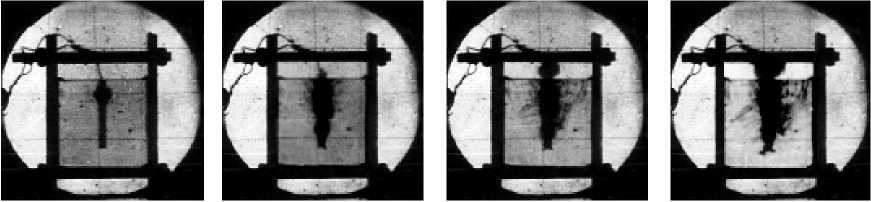
Рис 2. Кинограмма взрыва удлиненного цилиндрического заряда

Модели представляли собой кубики, размером 100 x 100 x 100, в центре которых имелись цилиндрические полости диаметром 7 мм и глубиной 75 мм, в них кооксиально размещался заряд диаметром 2 мм, высотой 50 мм и массой ТЭНа 1,4 г.

Для моделирования процесса взаимодействия волн напряжений от смежных зарядов к двум боковым граням модели прикладывались гладкие жесткие пластины. Процесс взрыва фиксировался высокоскоростной киносъемкой. Из кинограммы (рис. 2) видно, что скорость детонации заряда составляла 6000 м/с, а скорость истечения ПВ – 700-1000 м/с. Волны напряжений в модели распространялись со скоростью продольной волны данной среды. В результате интерференции волн напряжений от жестких границ (осей симметрии) образовывались направленные радиальные трещины, которые детерминировали раскол модели на две равные части. Средняя скорость развития магистральной трещины составляла около 2000 м/с, и процесс разрушения образца происходил за 25 - 10 -6 с. Следовательно, можно утверждать, что определяющую роль в развитии магистральной трещины играет взаимодействие волн напряжений, хотя при этом в полости зарядной камеры еще продолжают сохраняться газообразные продукты взрыва, что свидетельствует о квазистатическом процессе разрушения.