Математическая модель движения семян льна-долгунца в семяпроводе на основе применения нечеткой логики

Введение.

Посев льна-долгунца — технологически сложный процесс, требующий высокой точности дозирования и равномерности распределения семян [7] . Специфика культуры обусловливает ряд принципиальных ограничений:

• 1)     мелкий размер семян (масса 1000 шт. — 3-7г) повышает риск их

травмирования при механическом воздействии;

• 2)     высокая требовательность к равномерности высева — неравномерное

распределение приводит к конкуренции растений за свет и питательные вещества, снижая выход волокна и семян;

• 3)    чувствительность к глубине заделки — отклонение даже на 0,5-1 см критично для всхожести из-за слабого начального роста проростка;

• 4)    зависимость от влажности семян — при повышенной влажности возрастает адгезия к рабочим поверхностям, провоцируя забивание семяпроводов.

Эти особенности делают традиционные детерминированные модели посева недостаточно эффективными: они не учитывают стохастичность факторов (колебания воздушного потока, неоднородность семенного материала), что ведёт к:

• •    потерям семян из-за забивания семяпроводов;

• •    неравномерности распределения по площади;

• •    снижению полевой всхожести на 15-25 %.

Цель исследования — разработать математическую модель движения семян льна-долгунца в семяпроводе на основе нечёткой логики, обеспечивающую повышение точности дозирования и распределения за счёт учёта нечёткости входных параметров.

Разработанная модель может быть использована производителями посевной техники, агрохолдингами и научно-исследовательскими организациями при проектировании и настройке высевающих систем для льна-долгунца и других мелкосемянных культур.

Основная часть.

Посев льна-долгунца предъявляет жёсткие требования к технологическому процессу ввиду специфических биологических и физико-механических характеристик семян. Семена льна отличаются малым размером (3-5мм в длину и 1,5-2,5мм в ширину) и небольшой массой (3-7 г на 1 000 штук), что существенно осложняет их дозирование и повышает риск механического травмирования. Форма семян — овально-яйцевидная с заострённым концом — обусловливает анизотропию трения и склонность к заклиниванию в узких каналах семяпроводов. Важную роль играет коэффициент трения, который напрямую зависит от влажности: у сухих семян он составляет 0,25–0,35, а при увлажнении возрастает до 0,4–0,55 из-за усиления адгезии к металлическим и полимерным поверхностям. Кроме того, оболочка семян относительно хрупкая, а сами они обладают высокой гигроскопичностью — активно поглощают влагу из воздуха, что в процессе хранения и высева меняет их массу, объём и фрикционные свойства [6] .

Технология посева требует строгого соблюдения ряда параметров для обеспечения высокой полевой всхожести и равномерного стеблестоя. Глубина заделки должна находиться в диапазоне 1,5-2,5см: отклонение более чем на ±0,5см критично — при заглублении прорастание замедляется и проростки ослабевают, а при недостаточной глубине семя может пересохнуть и зародыш погибнет [5] . Норма высева составляет 5-6 млн всхожих семян на гектар (50-100кг/га) с точностью дозирования не ниже ±5% от заданной нормы [9] . Равномерность распределения также жёстко регламентирована: по площади коэффициент вариации межсеменного расстояния не должен превышать 15%, а по рядкам отклонение от заданной ширины междурядий допускается в пределах ±1 см. Скорость посева ограничена значением 8-10 км/ч — превышение этого порога ведёт к неравномерному распределению и травмированию семян. Наконец, состояние почвы должно обеспечивать мелкокомковатую структуру (диаметр агрегатов 1-5 мм) и плотность 1,1-1,3 г/см³ [7] .

Классические математические модели движения семян в семяпроводах, базирующиеся на механике сплошных сред, дифференциальных уравнениях и регрессионном анализе, демонстрируют ряд принципиальных ограничений, снижающих их применимость для посева льна-долгунца. Прежде всего, они не учитывают вариабельность влажности семян, которая в реальных условиях может изменяться от 10% до 11% [8] . Это напрямую влияет на коэффициент трения (рост на 30-50 % при увлажнении), аэродинамическое сопротивление (увеличение массы снижает скорость в воздушном потоке) и склонность к слипанию и забиванию, однако модели используют фиксированные значения параметров, что порождает ошибки в прогнозировании.

Ещё одно существенное ограничение — игнорирование колебаний воздушного потока в пневмосистемах. Давление и скорость воздуха варьируются из-за пульсации вентилятора, изменения длины и конфигурации трубопроводов, локальных сужений или расширений. В реальности поток турбулентен, а скорость семян колеблется на 10-20%, однако детерминированные модели предполагают стационарные условия, что приводит к неравномерности подачи и «провалам» в высеве.

Кроме того, классические модели не адаптируются к изменениям рельефа поля. На склонах угол наклона семяпровода меняется от –5° до +10°, что влияет на силу тяжести, действующую вдоль оси, и вероятность застревания семян в изгибах. Поскольку модели не предусматривают динамической корректировки параметров в зависимости от пространственного положения машины, возникают локальные перегущения или пропуски высева [4].

Также детерминированные подходы не учитывают неоднородность семенного материала: в партии присутствуют семена разного размера, формы и массы, что ведёт к сепарации по размерам в пневмосистеме и неравномерному распределению в рядке. При этом расчёты ведутся «в статике», без обратной связи с реальными условиями посева (влажность, давление, наклон) и без механизма адаптации к нештатным ситуациям (например, частичному забиванию семяпровода).

Разработаем модель, исходя из фиксированных значений входных лингвистических переменных, для начала стоит представить структурную схему нечеткого вывода представленного на рисунке 1.

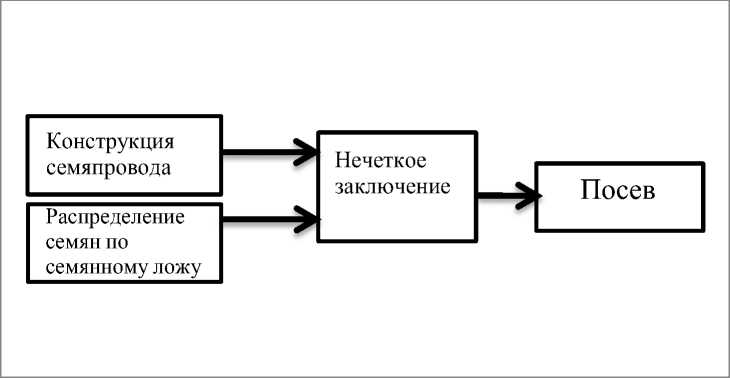
Рисунок 1 - Структурная схема нечеткого вывода

Далее определены основные параметры для создания математической модели

• 1)     влажность семян — умеренная (9-12 %);

• 2)    скорость воздушного потока — оптимальная (6-8 м/с);

• 3)     плотность посева — нормативная (30-50 тыс. семян/м²);

• 4)    шероховатость семяпровода — средняя (1-2 мкм).

На первом этапе сформируем базу нечётких правил, отражающую взаимосвязи между входными параметрами и выходными показателями. Правила строятся по схеме «ЕСЛИ<условие 1>И<условие2>ТО<вывод>» с использованием логического оператора И (min) для агрегирования условий [2] . Для заданных входных значений актуальны следующие правила, которые представлены в виде системы:

^r (W = ум) Л (V = опт) ^ S = стаб (D = норм) Л (R = ср) ^ U = выс < (V = опт) Л (D = норм) ^ Р = низ, (W = ум) Л (R = ср) ^ В = низ < (V = опт) Л (W = ум) ^ Т = мин Далее представлена расшифровка обозначений: W — влажность семян, %;

• V — скорость воздушного потока, м/с;

• S — скорость движения семени, м/с;

D — плотность посева (количество семян, размещённых на единице площади), шт/м2;

R — шероховатость семяпровода, мкм;

U — равномерность высева, %;

P — вероятность пропусков, %;

B — риск забивания, %;

T — травмирование семян, %.

Поскольку входные значения точно соответствуют диапазонам заданных термов, все пять правил активны со степенью истинности 1,0.

Перейдём к механизму нечёткого вывода. На этапе фаззификации определяем степень принадлежности входных параметров к нечётким термам. Для всех переменных она равна 1,0 (точное попадание в центр лунки) [1]. Далее выполняем агрегирование условий в каждом правиле через оператор min:

для Правила 1: min(1,0; 1,0)=1,0;

для Правила 2: min(1,0; 1,0)=1,0;

для Правила 3: min(1,0; 1,0)=1,0;

для Правила 4: min(1,0; 1,0)=1,0;

для Правила 5: min(1,0; 1,0)=1,0.

На этапе композиции нечётких множеств объединяем выводы всех правил через оператор max для каждого выходного параметра:

скорость движения семени: стабильная=1,0;

равномерность высева: высокая=1,0;

вероятность пропусков: низкая=1,0;

риск забивания: низкий=1,0;

травмирование семян: минимальное=1,0.

Дефаззификация — заключительный этап нечёткого логического вывода, в ходе которого нечёткие лингвистические оценки преобразуются в конкретные числовые значения, пригодные для практического применения [3] . Выбор метода дефаззификации зависит от типа выходной переменной:

• •    для непрерывных параметров (скорость, процентные доли) применяется метод центра

тяжести;

• •    для дискретных категорий (уровни риска, качественные оценки) используется метод максимума.

Рассмотрим применение этих методов к каждому из выходных параметров.

• 1.    Скорость движения семени Диапазон нечёткого   множества: 0,8–

• 1,2 м/с (лингвистическая оценка «стабильная»).

  /о 8 V*u(v)dv

V = ^82—— ~ 1,0 м/с,

/08 u(v)dv где μ(v) — функция принадлежности нечёткого множества «стабильная».

После вычисления интегралов (с учётом формы функции принадлежности) получаем:

v ~ 1,0 м/с

Прогнозируемая скорость движения семени составляет 1,0 м/с, что соответствует лингвистической оценке «стабильная».

Далее рассмотрим вероятность равномерного высева (непрерывный параметр). Диапазон нечёткого множества: 85–95%. Предполагая симметричную функцию принадлежности, центр тяжести совпадает с серединой диапазона:

p

равн

85+95

= 90%,

Вероятность равномерного высева оценивается в 90%.

Также стоит рассмотреть риск забивания.

Значения, которые применяются на данном этапе: «низкий», «средний», «высокий».

Входные данные:

• •    Степень принадлежности к «низкий»: μ низкий=1,0;

• •    Степени принадлежности к «средний» и «высокий»: <1,0.

Поскольку μ низкий достигает максимума (1,0), выбирается категория «низкий». Риск забивания семяпровода признается «низкий».

Далее травмирование семян. Диапазон нечёткого множества: 1–3%. Для симметричной функции принадлежности центр тяжести — середина диапазона:

Т = 1+3 = 2%,                            (4)

Уровень травмирования семян составляет 2%, что признается оценке «минимальное».

На основе дефаззификации получены следующие чёткие значения:

• 1.    Скорость движения семени: 1,0 м/с («стабильная»);

• 2.     Вероятность равномерного высева: 90% («высокая»);

• 3.      Риск забивания семяпровода: «низкий»;

• 4.     Травмирование семян: 2% («минимальное»);

Таким образом, модель прогнозирует оптимальный режим высева льна-долгунца при заданных условиях. Высокая равномерность распределения, минимальный риск забивания и травмирования подтверждают корректность выбранных параметров сеялки. Это позволяет рекомендовать указанные настройки (умеренная вар, оптимальная скорость потока, нормативная плотность посева, средняя шероховатость семяпровода) как базовые для практического применения.

Заключение

В ходе исследования разработана математическая модель посева льна-долгунца на основе нечёткой логики, решающая проблему низкой эффективности традиционных детерминированных подходов, которые не учитывают стохастичность ключевых факторов, что приводит к забиванию семяпроводов, неравномерному распределению семян и снижению всхожести на 15-25%. Модель интегрирует лингвистические переменные и функции принадлежности для учёта нечёткости входных параметров, описывает динамику движения семени через дифференциальное уравнение второго закона Ньютона с нечёткими коэффициентами трения и аэродинамического сопротивления, формирует базу правил типа «ЕСЛИ^И^ТО^» для прогнозирования скорости движения, равномерности высева, риска забивания и травмирования семян, а также применяет механизмы нечёткого вывода и дефаззификацию.