Математическая модель фильтрации канонических параметров спутника-ретранслятора при орбитальном движении

искусственных спутников Земли [11] при заданных начальных условиях сводятся к решению систем дифференциальных уравнений в кинематических или оскулирующих переменных, которые задают уравнение состояние относительно прогнозируемых канонических параметров СР на текущий момент времени. Фактически канонические параметры, полученные при экстраполяции из уравнения состояния, всегда отличаются от реальных из-за действия и неполноты учета возмущающих факторов, неадекватности расчетных моделей [2]. Повышение точности указанных методов возможно при добавлении к уравнению состояния дополнительной системы уравнений наблюдения, задающей в формируемой модели разнесенных измерительных сенсоров независимое правило оцени канонических параметров СР, с последующей фильтрацией получаемых значений состояния и наблюдения по выбранному критерию в обобщенной теории байесовской фильтрации [12; 25]. Подобные решения с применением калмановской модели фильтрации координат подвижного объекта рассматриваются в работах В.С. Черняка [13], D. Musicki, W. Koch [14], В.Н. Харисова, А.И. Яковлева, А.Г. Глущенко [15], Zhixin Liu, Yongjun Zhao, Dexiu Hu, Chengcheng Liu [16], K.C. H o [17] и др. Однако указанные исследования непосредственно не рассматривают задачу фильтрации канонических параметров СР и не учиты вают особенности фор- lm^^m © Полянский И.С. и др., 2019

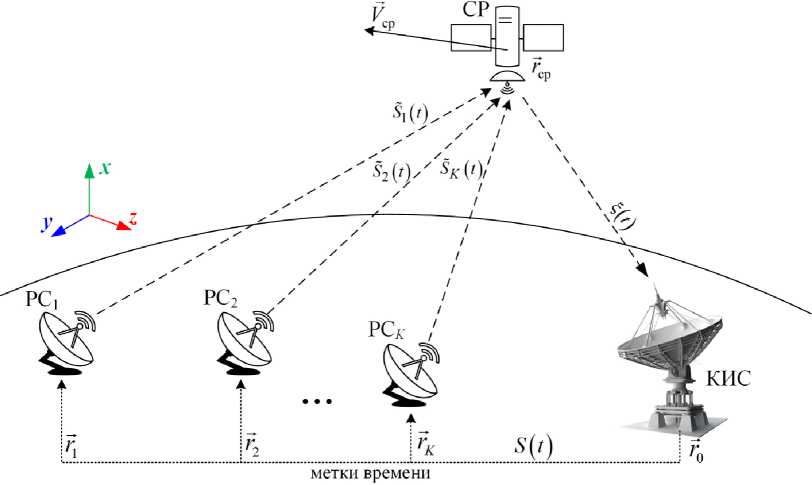
Рис. 1. Схема задачи фильтрации канонических параметров спутника-ретранслятора при орбитальном движении

мирования рекуррентных алгоритмических решений с определением матриц эволюции и перехода при линеаризации исходной модели. Последнее затрудняет построение адекватных математических моделей фильтрации канонических параметров спутника-ретранслятора при орбитальном движении. Устранение указанного недостатка является целью настоящей статьи.

С учетом анализа решений [1; 12–16] сформирована схема задачи фильтрации канонических параметров спутника-ретранслятора при орбитальном движении (рис. 1).

Основные объекты схемы: командно-измерительная система (КИС); спутник-ретранслятор (СР); K реперных станций (РС). Вектор параме-трое X ( t ) = { r _cp ( t ) , V _cp ( t ) } состояния СР является исследуемым векторным случайным процессом, который задает канонические параметры СР – положение — cp ( t ) и скорость V _cp ( t ) в момент времени t . Положения КИС и РС известны и характеризуются векторами ^— и * 1 ,..., г _к соответственно.

Реперные станции k -е передают тестовый сигнал S ( t ) на спутник-ретранслятор с частотой fk® ( t ) . Передача сигнала выполняется синхронно с помощью меток времени спутниковых радионавигационных систем ГЛОНАСС и/или GPS [1]. На входе приемника СР наблюдается сигнал S k ( t ) ( k = 1, K ) , различие которого от исходного S ( t ) обуславливается воздействием помех среды распространения радиосигнала и смещения fk® ( t ) на величину доплеровского сдвига частоты A fk® ( X , t ) на участке распространения от k -й

РС до СР. Ретрансляция сигнала S ( t ) k -й РС спутником связи осуществляется на частоте fk® ( t ) + + A f B ( X , t ) + A f ^cp ( t ) , где A f ^cp ( t ) - частота переноса СР на линию вниз (участок от СР до КИС), которая формируется из суммарной частоты всех гетеродинов приемника и передатчика СР. На входе приемника КИС сигнал S ( t ) k -й РС наблюдается на частоте fk® ( t ) + A fk® ( X , t ) + A f ^cp ( t ) + A fk^H ( X , t ) , где A f ^вн ( X , t ) - доплеровский сдвиг частоты на участке распространения от СР до КИС. На выходе приемника КИС формируется суммарный сигнал

K                          —

^ ( t ) = Е A k ( t ) ^S ( t ^-T k ( ^X , t ) ) e ^ ^ ^{+ u} ( t ) , k = 1

составленный из сдвинутых по временному T k ( X , t ) и частотному A F ^ ( X , t ) параметрам сигналов k -х реперных станций, затухания A k ( t ) сигнала на участке распространения k -я РС–СР–КИС и шума и ( t ) . Шумовой параметр и ( t ) в рассматриваемой математической модели непрерывного канала связи определяет помехи среды распространения на линиях вверх и вниз (соответствующие участки от k -й РС до СР и от СР до КИС).

Величина времени прихода Tk(X, t) сигнала S(t) от k-й РС на КИС складывается Tk (X, t) = = тk (X, t) + 5Т(t) из ошибки 5Т(t) измерения и истинного времени тk (X, t) прихода на КИС сигнала от k-й РС. Значение тk (X,t) удовлетворяет тождеству тk (X, t) = c^1 (Ik

—*

^{- F c}p

⁽ t ^{) +} |^— cp ⁽ t ) " ^— o|) ,

где c – скорость света в вакууме.

Ошибка 5 k ( t ) обуславливается ионосферной и тропосферной ошибками измерения на линиях вверх и вниз – соответствующие участки от k -й РС до СР и от СР до КИС и ошибкой синхронизации передачи сигналов РС по меткам времени.

Величина частотного сдвига A F j ( X , t ) принимаемого КИС сигнала S ( t ) к -й РС от СР определяется ^{A F} к ( ^X ' t ) = fk^ ( t ) ^{+ A} f^ ( ^X ’ t ) ^{+ A f CP} ( t ) ⁺ + A ff ( X , t ) +A f ^киc ( t ) = A f k ( X , t ) + 5 к ( t ) ,

где A f ^киc ( t ) - суммарная частота всех гетеродинов приемника КИС; A f k ( X , t ) и 5 / ( t ) - истинный частотный сдвиг принятого КИС сигнала

обусловленное действие сил (влияние нецентри-рованного поля тяготения Земли, притяжение третьих тел, давление солнечного света, наличие атмосферы и др. [2; 7]) на СР; M c T ( t ) - транспонированная матрица M ct ( t ) = d M ct ( t )/ dt ; M ct ( t ) -матрица преобразования небесной системы координат в Земную. Предполагается, что вычисление элементов матрицы M ct ( t ) выполняется численно с применением интерполяционного метода, например Лагранжа. Производная произвольной функции f ( x ) в таком случае будет определяться соотношением

S ( t ) от к -й РС и ошибка измерения A f k ( X , t ) соответственно. Значение A f k ( X , t ) удовлетворяет

тождеству

df x ^{2 L}

4(r " E f ( ^A x ' ) dx     l = 0

х

^{A f} k ( ^X , t ) =

r

= «V ( t ) f k B^B

2 L <

l

-

A X.

l ₁

M t H + f BH

Iъ(t)-k\    k

0 ^- ■ ⁽ t ) ' I - ^- ' Cp ⁽ t t

^Х Х ' 1 * ' ^;

' . = 0 к ' , = ' ,

]2П ¹ x ^-A x l 2 V^{( A X} ' ^-A x l 2 ) ; 1 2 = 0 I ¹, l 2 = l ^v l 2 = ' 1 ,

где fk" = В [ f k " ] и fk*" = E [ fk"" = f k ” + A f "^p ] средние номинальные значения передачи сигнала S ( t ) k -й РС на линиях вверх и вниз соответственно.

Ошибка 5 { ( t ) обуславливается нестабильностями гетеродинов передатчиков k -х РС, СР и приемника СР, КИС.

Учитывая содержательное описание схемы фильтрации канонических параметров СР при орбитальном движении, сформулируем основные допущения и ограничения, выделяемые при решении задачи математического моделирования.

1. Математическая модель пространственного движения спутника-ретранслятора формируется в земной системе координат и задается в кинематических параметрах:

где A x ' = x + A ( l - L ) ; A - шаг численного дифференцирования; 2 L – порядок интерполяции.

• 2.    Правила вычисления элементов Ф ( t ) , M ct ( t ) известны и могут быть реализованы по алгоритмам, представленным в [18].

• 3.    Ошибки измерений 5 k ( t ) , 5 jf ( t ) и эволюции A v ( t ) , A r ( t ) , характеризующие флуктуацию случайных параметров, являются случайными вели-

чинами, которые распределены по нормальному

^dV cp ( t )/ ^dt = ^M ct ( t ) ^ ( t ) ^- ^ | r p ( t )| 3 r p ( t ) ) - M ct ( t ) M C T ( t ) V cp ( t ) + A V ( t ) ;

dr p ( t )/ dt = V ^ cp ( t ) ^-

^{- M} ct ⁽ t ) M C T ⁽ t ) r p ⁽ t ^{) + A} r ⁽ t ) ,

-

где ц = GM - гравитационный параметр Земли; G = 6,6719 ■ 10 ^{- 11} м 2/ ( кг ■ c ² ) - постоянная поля тяготения Земли; M = 5,974227218225421 ■ 10²⁴ кг -масса Земли; A _v ( t ) и A r ( t ) - векторные функции, которые характеризуют случайных характер

изменения вектора скорости и положения СР соответственно; Ф ( t ) - возмущающее ускорение,

закону.

4. Особенности реализации многостанционного доступа РС к частотно-энергетическому ресурсу СР выносятся за рамки формируемой математической модели.

Для формирования обобщенной математической модели фильтрации канонических параметров СР представим X ( t ) непрерывным векторным марковским процессом, эволюция которого в общем виде определяется из уравнения

состояния:

X _t = o ( X _t , t ) +iv _t , —► d X* где ^X t ^X ( t ) ; ^X t = - dt -;

o ( X _t , t ) - вектор сноса;

^v t = ’V ( t ) - белый гауссовский вектор-шум при E[ V_t ] = 0 и cov [ iv t ] = Q t , наблюдаемый по пра-

вилу

ⁿ t = ^A ( ^X t , t ) ^{+ v} t , ⁽⁶⁾ где n t =n ( t ) ; v t = v ( t ) - белый гауссовский вектор-шум при E[ VW t ] = 0 и cov [ v t ] = R t ; X ( X _t , t ) -

функции измерения канонических параметров СР

по принимаемым сигналам РС.

С учетом заданной постановки задачи фильтрации в соотношениях состояния (5) и наблюдения (6) вектор сноса Ф ( X _t , t ) и вектор-шум w_t для X ( t ) = { r _cp ( t ) , V _cp ( t ) } определяются из выражения (3) соответствующими соотношениями:

' V cp ⁽ t ^{) —} M ct ⁽ t ) M t ⁽ t ) ^- cp ⁽ t ) '

мального правдоподобия взаимной функции неопределенности (ВНФ), которое представлено, например, в [19].

Решение системы нелинейных уравнений (8)

предлагается выполнять численно, например методом Ньютона [20], при составлении приближения наблюдаемого вектора состояния n j СР итерационным вычислением

- Г n + 1 1 - Г n 1     _ 1 Г - Г n 1 ^ - Г - Г n 1 'I

П у      -Пу ^J — н I П у ^J , t j I G I П у ^J , t j I ,

4 ( X . , t ) =

M „ (t) » (t)

—

"     ^- cp ( t )

I-cp ( t )

—

-    |4 ( t ) )

r

" t t ^A V ( t ) J ,

— M ct ( t ) M C T ( t ) V cp ( t )

где n e [ 0; N J , N - максимальное число итера - Г 0 1 -        Г - Г n 1 )

ций; n j =X j ; H In j , t j I — матрица Якоби для

Г - Г n 1    )

системы функций G I n j ^J , t j I • Основные эле

а функция измерения Y ( X _t , t ) задается решением системы из 6 уравнений, составленных тождествами (1), (2), и при обозначениях

G k ( ^{X ,} t ) = k ^{— -} cp ⁽ t ) + |^- cp ⁽ t ) ^{— -} 0 1^— c ^T k ( ^{X ,} t ) ^,

Gk (X,t) = ^p(t)x x ' fT   -cp (t) — -k + f“ -0 — -cp (t) ) c

_V ^A f k ( ^{X ,} t ) |- p ( t ) — ^- k | ^A f k ( ^{X ,} t ) |^- 0 — ^- cp ( t )| J ,

менты матрицы H ( X , t ) при обозначениях ^- _cp =

^cp^cp^cp^{T -} k k k ^{T -}       0 0 0 ^T

= ( ^r 1  • ^r 2   • ^r 3   ) •   r k = ( ^r 1 • ^r 2 • ^r 3 ) •   ^r 0 = ( ^r 1 • ^r 2 • ^r 3 ) •

V _cp = ( V 1 ^cp , V 2 ^cp , V 3 ^cp ) задаются через

частные производные:

следующие

задаваемых в виде

( G k ( ^X , t ) ^G k 2 ( ^X , t ) ^G k 3 ( ^X , t )

T

• - ) G f ( ^X • t ) G f ( ^X • t ) ) =              ⁽⁸⁾

= G (X, t ) = 0, где k1,k2,k3 e[1;KJ : k1 ^ k2 ^ k3.

Приняв дополнительное ограничение о том, что на длительности A t элементы вектора X _t при достаточно медленном изменении постоянны, разобьем интервал наблюдения [ 0, T ] на тактовые подынтервалы t еГ t j , t j + 1 J ( a t = t j + 1 — t j ; j = 1, N t ; N t =^ Г /A t J ) и перепишем уравнения состояния (5) и наблюдения (6) в виде

X j = Ф ( X j , t j ) + « j                                  (9)

П j = Y ( X j , t j ) + v j ,                                         (10)

^{d G}k/ ^{d r} 1, p ,3 = ( ^r 1, p ,3    ^r 1,2,3 ) |- k   - p|    ⁺

⁺ ( ^Г 1Д3 ^{— r} 102,3 ) |^-cp ^{— -} 0| 1 ;

d G k = — f k"	r cp r 1,2,3    r 1,2,3			—*       —* r cp — r k	- -V	V 1C, p ,3	>
d r ,-y3     A f k	V	- k — - cp	2	r cp - r k	cp	r cp - r k	7

+

Г rbh rcp _r0   - _- fk    r1,2,3   r1,2,3 rcp   r0 V V1,p,3 Afk V I-, — -cp2 I?cp -?»l cp -cp — - 1 f г bb rcp           ? bh rcp _r0„ dGk   _ fk '1,2,3   r1,2,3   fk '1,2,3 r1,2,3

^d ^,3    ^{A f} k   |^- k ^{— -} cp|     ^{A f} k   |^-cp ^{— -} 0|

Прогнозирование состояния Xj+1 СР в момент времени tj+1 осуществляется решением обыкновен--    - - ного дифференциального уравнения Xj — OlXj,tj) из (9) с применением явного метода Рунге – Кутты [21]:

s

X j + 1 —X j + h Z b i к ji ;

-   -      -   -      -    -      -   - где Xj   л|tj);  nj = n(tj);  «j = «(tj); vj = v(tj).

Г -- ^K ji = ^{ф X} j

V

С учетом заданного дополнительного ограни-

^K j 0 = ^{Ф (X} j , t j ) ,

i = 0

i — 1

+ h Z aii,K ji', tj + cih i '=1                      J

чения оценка частотных

т k ( X j , t j ) параметров

A f k ( X j , t j ) и временных

в (8), принимаемого КИС

сигнала k -й РС, выполняется по правилу макси-

где h < A t - величина шага по временной сетке; s - число этапов численной схемы; a_ti, , b i , c i - вещественные коэффициенты, которые могут быть заданы по правилам из [21].

Рекуррентное вычисление (11) формирует приближенный вид Т£ (Xj, tj) функции измерения Т (Xj, tj) и совместно с численным решением (13) позволяют задать нелинейную задачу фильтрации канонических параметров СР при орбитальном движении:

^X j + 1 = ^X j ^{+ Ф} £ h ^(X j , t j ^{) +} w j + 1 ; ^П j + 1 = ^T £ n ^(X j + 1 , t j + 1 ^{) + V} j + 1 .

где

s       f         i - 1

^Ф £ h ( ^X j , t j ) = h S b i ^{Ф X} j ⁺ h Z a ii '^K ji ', t j ⁺ c i h i = 0       (         i '= 1                     ,

Выполним линеаризацию сформированной модели (14) при разложении функции эволюции X j + Ф _£^ ( X j , t j ) и функции измерения Т _£ ( X j , t j ) в ряд Тейлора в окрестности точки X j по первому члену:

—*                —*       —*

^X j + 1 = A j ^X j ⁺ B j ⁺ w j + 1 ;

—— n j+1 = Cj+1X j+1 + Dj+1 + vj+1,

■          ■    ■   ■           ■     ■ где Aj = JM (X j, tj)+E; Bj =ф£ h (X j, tj)-JM (X j, tj )X j; - Jm (Xj, tj )Xj;    Jm (Xj, tj)   - матрица Яко би для системы функций <—>£^ (Xj, tj); Dj+1 = = -H 1 (X j+1, tj+1) G (X j+1, tj+1) + J s (X j+1, tj+1 )X j+1; Cj+1 = E- Js (Xj+1, tj+1); Js (Xj+1, tj+1) - матрица Якоби для системы функций H-1 (Xj+р tj+1) G (Xj+1, tj+1); E - единичная матрица. Элементы матриц Jм (Xj, tj), Js (Xj+1, tj+1) предлагается вы- числять численно с применением интерполяционного метода Лагранжа по заданному правилу (4).

Разработанная математическая модель (14) с учетом правила (15) по ее линеаризации позволяет применить известный алгоритм расширенного фильтра Калмана [22; 25] с использованием современных численных методов [26–28] для решения задачи оптимальной фильтрации канонических параметров СР при орбитальном движении.

Для практического обоснования сформированного решения в Mathc a d проведено м атематическое моделирование рассматриваемой задачи. Исходные данные вычислительного эксперимента выбраны следующими.

• 1.    Параметры СР: Ямал-401 (номер спутника в базе NO R AD 40345); номер вит к а на момент эпохи 1605; начальное время и дата моделирования 12 часов 40 минут 43 секунд 6.04.2019; длитель-

  ность измерений 2 дня; эксцентриситет орбиты 0,0000373; наклон орбиты 0,00025481807079117 рад; долгота восходящего узла 3,3725276388966745 рад; аргумент перигея 4,208400724261799 рад; средняя аномалия 0,7031373050924515 рад; частота обращения 1,00271746 обор./день; значения первой и второй производных среднего движения по времени –0,00000231 и 0 соответственно.

• 2.    Параметры КИС: широта 52 ° 47'54’’; долгота 36 ° 04'42’’; высота над уровнем моря 0.

• 3.    Параметры РС: число РС K = 4; f ^^B = = 5866 МГц; f ^^B = 3541 МГц; B = 20 кГц; широта РС №1 55 ° 45'07''; долгота РС №1 37 ° 36'56''; высота над уровнем моря РС №1 0; широта РС №2 56 ° 51'27''; долгота РС №2 60 ° 36'44''; высота над уровнем моря РС №2 0; широта РС №3 56 ° 29'51''; долгота РС №3 84 ° 58'27''; высота над уровнем моря РС №3 0; широта РС №4 54 ° 42'23''; долгота РС №4 20 ° 30'39''; высота над уровнем моря РС №4 0.

• 4.    Параметры модели состояния СР: поверхность Земли аппроксимируется геоидом EGM2008; возмущение параметров орбиты в модели состояния СР задано притяжением центрированного поля Земли, Луны и Солнца; возмущение параметров орбиты в реальной модели состояния СР дополнено давлением солнечного излучения и нецен-трированным притяжением Земли (использованы алгоритмические реализации из [18]).

Для выбранных параметров среднеквадратическая ошибка за время наблюдения модели состояния СР по положению составляет ст r = 94,14 м, а по скорости - ст _у = 1,495 ■ 10 ^{- 6} м/с.

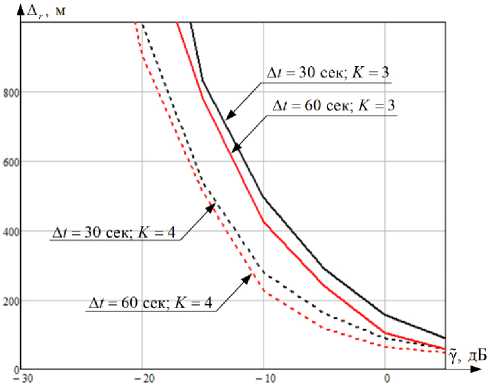
На рис. 2 приведены зависимости среднеквадратической ошибки оценки канонических параметров СР при орбитальном движении от K , А t и Y , усредненной на заданном интервале наблюдения по 100 расчетам.

Результаты проведенного моделирования подтверждают работоспособность и результативность разработанных алгоритмических решений. По данным апостериорных исследований (рис. 2), сформированное алгоритмическое решение фильтрации канонических параметров СР при орбитальном движении относительно погрешностей экстраполяции и наблюдения в среднем дает возможность снизить среднеквадратическую ошибки оценки в 1,78 раза. Предложенная линеаризация в модели фильтрации при уточнении особенностей формирования рекуррентных алгоритмических решений с определением матриц эволюции и перехода с минимальными вычислительными

а )

б )

в )

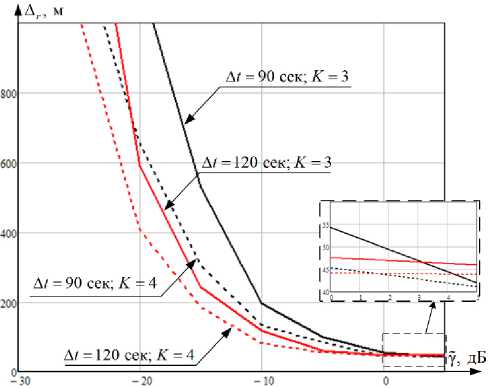
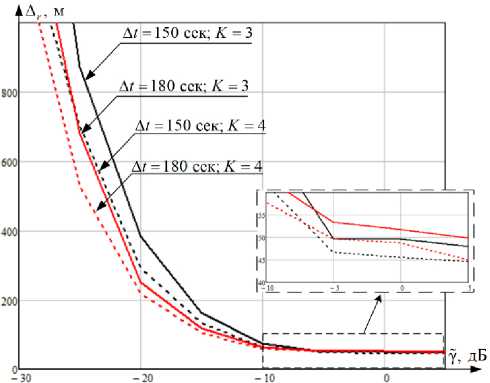
Рис. 2. Графики зависимости среднеквадратической ошибки оценки канонических параметров СР при орбитальном движении от K , A t и Y

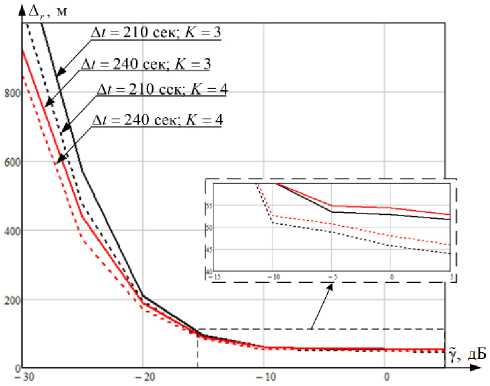
г )

затратами позволяет снизить накопление ошибок экстраполяции при увеличении времени наблюдения с относительно большой ошибкой наблюдения. Также апостериорно полученные зависимости (рис. 2) среднеквадратической ошибки оценки канонических параметров СР позволяют сформировать рекомендации по использованию конкретного числа реперных станций для заданных длительности интервала дискретизации и отношению сигнал/шум принимаемого тестового сигнала.