Математическая модель формирования видеоданных, получаемых с использованием сканирующей съемки
Автор: Кузнецов Павел Константинович, Мартемьянов Борис Викторович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Механика и машиностроение
Статья в выпуске: 6-1 т.16, 2014 года.
Бесплатный доступ
Рассматривается вопросы формирования видеоданных, получаемых при сканирующей съемке сцены с помощью ПЗС матриц, работающих в режиме временной задержки и накопления. Построены точная и упрощенная математические модели возникновения смаза изображений при указанном виде съемки. Показаны области применимости предложенных моделей.
Дистанционное зондирование земли, сканирующая съемка, смаз изображений, параметры смаза
Короткий адрес: https://sciup.org/148203519
IDR: 148203519 | УДК: 004.932
Текст научной статьи Математическая модель формирования видеоданных, получаемых с использованием сканирующей съемки
мой (ИС) на ПЗС матрицу, накопление ЗП достигает своей цели: увеличивается отношение «полезный сигнал/шум».
Возможная несогласованность работы аппаратуры ОЭП и СУС, проявляющаяся в несовпадении векторов СПЗ и СДИ, приводит к искажению формируемых видеоданных. Если такое несовпадение существует, то каждый пиксел ПЗС матрицы накапливает сигнал с некоторой вытянутой по форме площадки изображения, размеры которой больше площади входной апертуры пиксела ПЗС матрицы. Поскольку накапливаемый ЗП переносится вдоль столбцов в пикселы последующих строк матрицы, то в процессе продвижения ЗП по матрице размеры указанной площадки на изображении увеличиваются, то есть смаз формируемых видеоданных «накапливается». В результате в видеоданных появляется искажение, имеющее вид ориентированной в определенном направлении размытости наблюдаемого изображения, что, естественно, ухудшает этого изображения.
Далее, там, где это не приводит к путанице понятий, видеоданные мы также будем называть «изображением». В частности, будем говорить о «смазе изображения», понимая под этим смаз, накопленный в видеоданных.
Предложенная ниже математическая модель имеет основной целью определение характеристик и параметров смаза изображения.
МОДЕЛЬ ФОРМИРОВАНИЯ ВИДЕОДАННЫХ
Рассмотрим процесс формирования видеоданных при съемке наблюдаемой сцены.
Обозначим №у)энергетическую функцию распределения освещенности изображения (ФРО), сформированного ИС на плоскости изоб- ражений (ПИ), на которой установлены ПЗС матрицы ОЭП.
.
ПЗС матрица регистрирует изображение, накапливая энергию освещенности в ячейках матрицы в виде ЗП, и преобразует их в видеосигнал. В процессе регистрации изображение Е(х,у) движется по ПИ. Движущееся изображение представляется, при математическом моделировании, с помощью динамической ФРО:
, где время ;
– компоненты вектора СДИ:
.
Требуемое время накопления ЗП обеспечивается использованием режима ВЗН. В режиме ВЗН время экспозиции определяется количеством q строк накопления (активно работающих строк накопления) в ПЗС матрице.
Здесь считается, что элементарная ячейка ПЗС матрицы имеет форму квадрата со стороной [мм] ( – «характерный размер» ПЗС ячейки). Положение отдельной ПЗС ячейки в пределах матрицы (рисунок 1) определено парой целочисленных координат , где – номер столбца, ; – номер строки
Q" e {l,...,m})ПЗС ячеек матрицы.
ПЗС матрица в режиме ВЗН работает тактами, длительность которых обозначена как . На интервале длительности каждого такта ЗП во всех ячейках матрицы получают дополнительные заряды и в конце такта переносятся из каждой ячейки с номером в ячейку с номером
. Строка ПЗС матрицы с номером является выходной строкой матрицы. Заряд, накопленный в ее ячейках далее не переносится, а преобразуется в видеосигнал.
На рис. 1 схематично представлена структура ПЗС матрицы, расположенной в ПИ, и «привязанная» к ней система координат (СК).
Начало СК ((x,y) = (0,0))совпадает с центром пиксела(i./) = (1,1)ПЗС матрицы. Ось этой системы проходит через центры пикселов выходной строки матрицы и ориентирована в сторону возрастания номеров столбцов. Ось проходит через центры пикселов столбца с номером 1 и ориентирована в сторону возрастания номеров столбцов.
На рис. 1 использованы следующие обозначения:
– вектор СДИ; – вектор средней СПЗ ПЗС матрицы, ориентированный точно вдоль столбцов ПЗС матрицы, то есть параллельно оси Oy СК, но в противополож- ном направлении; осреднение скорости произво- дится за время перемещения зарядового пакета от ячейки до ячейки .
– область (окно) анализа на ПИ, границы которой совпадают с границами входной апертуры фоточувствительной зоны отдельной ячейки ПЗС матрицы. Здесь считается, что окно анализа имеет форму квадрата, координаты границ которого имеют значения: по оси Ox –
[мм], по оси Oy –
5Q- 1 + 0,5) [мм]. Далее окно анализа
будем называть « апертурой пиксела
» ПЗС матрицы.
Зарядовый пакет (ЗП), пересылаемый по ячейкам столбца с номером , обозначим как
. , где и – идентификаторы конкретного ЗП,
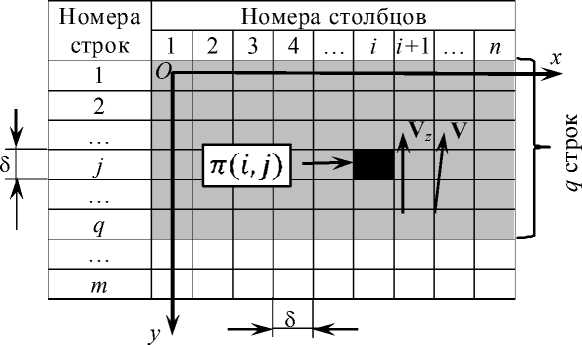
Рис. 1. Система координат плоскости изображений с привязкой к ПЗС матрице
находящегося на такте у работы ПЗС матрицы в выходной ячейке (i, 1) и к моменту окончания такта 6 готового к преобразованию в видеосигнал. Собственно преобразование Ch(e, l,j3 в видеосигнал осуществляется на такте с номером 5 + 1;
] – номер ПЗС ячейки в столбце
1
, в которой находился данный ЗП на такте с номером (6-J + l), 1
Номер такта работы ПЗС матрицы отсчитывается с момента начала съемки маршрута,
SeU,..,©}, 0– количество строк в видеоданных; 0 обычно принимается, для простоты, равным количеству тактов, отработанных ПЗС матрицей в процессе съемки маршрута. Заметим, что количество полноценно сформированных строк изображения будет не более, чем 0 — q + 1 , поскольку на формирование первой из них должно быть затрачено Q тактов.
Зарядовый пакет накапливается тактами. Первый такт накопления происходит в ячейке (l, Q ) и совпадает по времени с тактом (8 - 9 + 1)работы ПЗС матрицы. Далее ЗП, в процессе своего накопления, проходит последовательно все активированные для накопления строки ПЗС матрицы, заканчивая процесс накопления в строке / = 1 (ячейка (7, -0). То есть в процессе накопления ЗП индекс j пробегает значения от Q до 1. Номер такта накопления обозначим как A: . Тогда j = q — к + 1.
В принятых обозначениях итерационная процедура накопления ЗП <Мв, i,j) может быть представлена в виде:
j(k) = q — k + 1 ,
=
= Ch(O,i, (j(k) + 1)) + e(6, iJQO) , (1)
1 < к < q, начальный заряд ЗП: Ch(6, i,q) = 0;
где e(9,i,j(k')) – дополнительный заряд, накопленный в ЗП в ячейке (U(k)) на такте к накопления на интервале времени №-j(k)), т(5 -КЮ + П].
Здесь считаем, что самый первый такт 5 = 1 работы ПЗС матрицы приходится на временной интервал [0, T].
Из (1) следует, что зарядовый пакет
Ck(0, i, 1), снимаемый с выходной ячейки C^ 1) матрицы в момент времени T0 , может быть вычислен как сумма дополнительно накопленных зарядов :
Ch^d, i, 1) = Z^=1) e(5, i,j(k)) , (2)
Видеосигнал
1&8) :
получается оцифровыванием зарядового пакета (2):
Ki,e) = NAD(ch(e,i,i)), (3) где ^AD ( ) – оператор преобразования электрического заряда в цифровой целочисленный код; N. – максимальное значение используемого в аппаратуре цифрового кода; в рассматриваемой аппаратуре используется 10-разрядный двоичный код, поэтому Nm_ = 1023. Важным свойством оператора Nad О является его монотонность.
Рассмотрим процесс накопления дополнительного заряда e^Q, t,]3 .
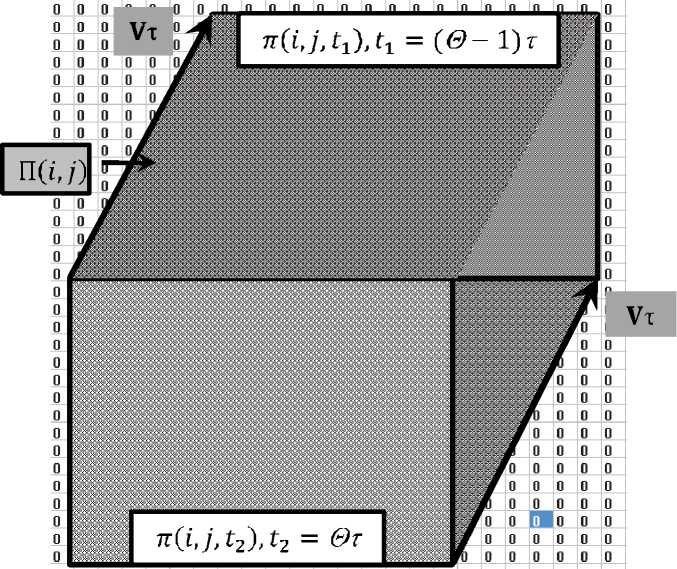
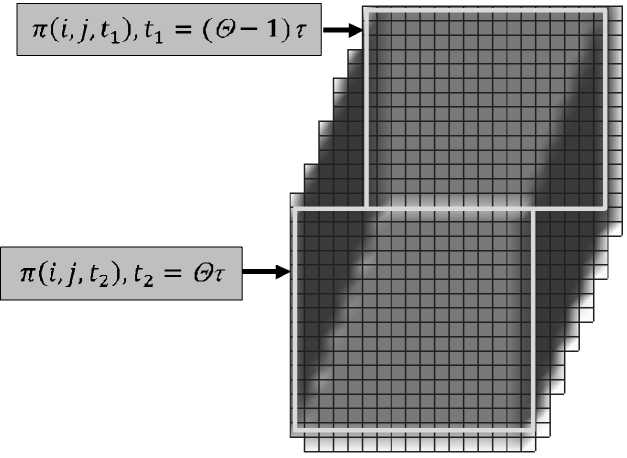
На рис. 2 показан процесс формирования областей, на которых изображение интегрируется в пространстве и времени при накоплении заряда e(6,i,j(k)). Прямоугольником lEUaOT) показано положение апертуры ПЗС ячейки UJOT) на плоскости изображения в начале такта накопления с номером k: 1 < к < q, то есть в ячейке(i,j) = (i,q-k + l).
Другими прямоугольниками, обозна- ченными как n(i,j(k),t), показаны проекции этой апертуры в моменты времени t ((5 -q + к - 1)t < t < (5 - q + к)т)на изображение Е(х,у), сдвинутое за счет его движения по плоскости изображения.
Сдвиг изображения на момент времени t определяется вектором сдвига
, sx(t) = vt, sy (t) = ut
где
В принятых здесь обозначениях положение апертуры ^(ij) совпадает с ее проекцией 7r(ij‘, t) в момент времениt = T(5-;)на изображение .
Объединение n(5,t,;) всех областей
7r(ij> t): ((5 - q + к - 1)t < t < (5 - q + к)т)
– это фрагмент (площадка) изображения E(x,y) , энергия облучения которого накапливается за время одного такта работы ПЗС матрицы в ее ячейке :
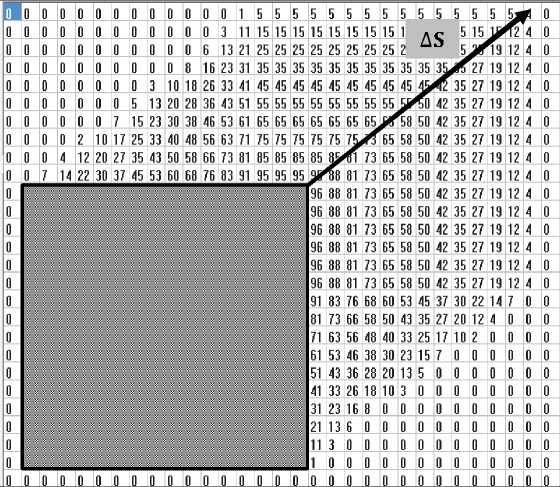
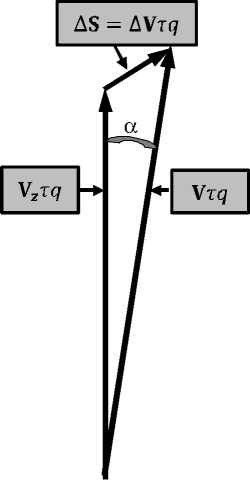
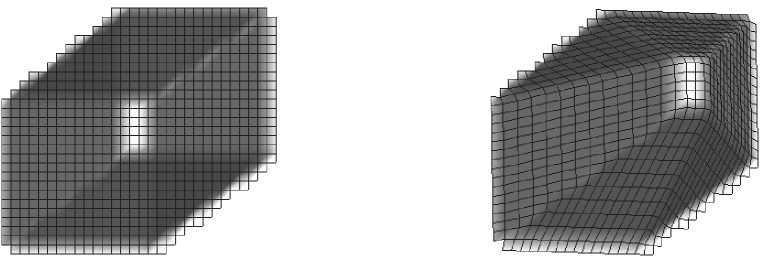
nC^li 5 ) — 0(ti где tl = (5 — q + к — 1)т, Как следует из рис. 2, дополнительный заряд, накопленный на такте , может быть вычислен по соотношению: , (4) где – коэффициент преобразования световой энергии в электрический заряд. Двойной интеграл, входящий в (4), может быть вычислен повторным интегрированием: t= те Рис. 2. Формирование области П(i,j) определения ядра K(i, j, x, y) смаза t= т(0-1) ^(ij'№) n(l,j(k), t) =. Величины являются парамет рами преобразования (1 - 4). Массив видеоданных образу ется при переборе значений переменных , в диапазоне . Ви- деоданные получаются как результат сканирования ПЗС матрицей изображения подстилающей поверхности на временном интервале . При этом следует учитывать, что первая строка видеоданных может быть сформирована только на такте с номером q, поскольку для формирования строки видеоданных необходимо затратить q тактов для накопления заряда. В случае, когда , то есть когда движение изображения не полностью компенсировано движением зарядовых пакетов, видеоданные массива содержат искажения, называемые «смазом» изображения. Формально эти искажения моделируются в (4) применением операции интегрирования по времени движущегося изображения. Как следует из (1, 3, 4) величина искажений определяется временем накопления заряда в ПЗС ячейке, количеством использованных строк накопления заряда и значениями компонент вектора СДИ. ОПЕРАТОРНАЯ ФОРМА МОДЕЛИ ФОРМИРОВАНИЯ «СМАЗАННЫХ» ВИДЕОДАННЫХ Использование выражения (4) для численного моделирования не оправдано из-за завышенной вычислительной сложности алгоритмов, реализующих преобразование (4). Завышенный объем вычислений обусловлен применением в (4) процедуры многократного интегрирования данных с одних и тех же фрагментов изображения. Операции многократного интегрирования мож- но избежать, если использовать оператор интегрального преобразования, вытекающий из (2), с ядром К^х.У) специального вида: , (6) , [tl(x,y),t2(x,y)]:(t E [tl(x,y),t2(x,y)])O . Содержательно At(Xy) – длительность максимального интервала времени , в течение которого точка , зафиксированная на изображении №y) в момент времени , двигаясь вместе с изображением по закону , на интервале вре мени [tl(x,y), t2(x,y)]остается в пределах области, накрываемой пикселем . То есть – время экспозиции указанной зафиксированной точки на апертуру ПЗС ячей ки . Общий вид предлагаемого интегрального преобразования эквивалентного преобразова- нию (4) следующий: eLi>j> 6^ — kz ffnQ ^ K^j) (x, y) , (7) где – область на плоскости изображения такая, что для заданного пиксела выполняется: , (8) где [tl(x,y),t2(x,y)]: УПРОЩЕННАЯ МОДЕЛЬ ФОРМИРОВАНИЯ ВИДЕОДАННЫХ Область ПО,У) – это такая область, энергия облучения которой накапливается в пикселе (l, J ) за время одного такта переноса зарядов длительностью . Типовая ПЗС матрица, составляющая ОЭП космических аппаратов ДЗЗ [Бакланов], имеет размерность m=128 строк на n=1024 столбцов ПЗС ячеек при размере элементарной ячейки (пиксела матрицы)6X6= мкм. При работе матрицы в режиме ВЗН количество строк q накопления может задаваться из некоторого набора целых значений q< 128. Приведенная ниже модель формирования смаза будет иллюстрироваться на примере такой типовой матрицы. На рис. 3а представлен пример ядра Преобразование (7) затруднительно использовать в общем случае для выявления и получения аналитических оценок параметров смаза. Поскольку такие оценки весьма полезны для практики, построим упрощенную модель формирования смаза. С целью построения упрощенной модели смаза будем считать, что ЗП накапливается в ячейке (i,j ) матрицы, координата } которой изменяет свое значение не скачкообразно, а плавно. То есть будем считать, что зарядовый пакет в процессе накопления заряда движется вдоль столбца матрицы с постоянной скоростью, определяемой вектором средней скорости движения ЗП Vz = (O,uz). При таком упрощении заряд смаза накапливается на площадке ПП,р, определяемой разностью AV векторов V- и : AV = V-V , (9) или в координатной форме записи определенного на площадке С учетом (9) ФРО движущегося изображения запишется в виде: П(0,м) для случая, когда за время T такта накопления заряда изображение сдвигается по направлению оси Ox на 0,4 пиксела, по направлению оси Oy – на 1 пиксел. На рис. 3а и 3б шаг сетки – это 1 / /16 °. Цифры в клетках сетки – это значение функцииК^^.У), выраженное в процентах от длительности интервала T. На рис. 3б функция К^х,^представлена раскрашенной полиго- нальной поверхность, изображенной в аксономет- рической проекции. При этом высота точки поверхности над точкой(x.y)СК Oxy прямо пропорци- ональна значению К^Ух.у) , то есть прямо пропорциональна времени экспозиции точки Cyy)на ПЗС ячейку C^ j j ) . Яркость точки поверхности пропорциональна модулю проекции нормального вектора к поверхности в этой точке на ось Oz, ориентированную перпендикулярно показанной на рис. 1 плоскости Oxy СК. Яркость используется здесь только для придания наглядности пространственной форме. Заметим, что даже в идеальном случае точного совпадении средней скорости движения зарядового пакета V со значением компоненты V вектора V СДИ сдвиг изображения по направлению оси Oy за время T равен точно 5. = = E(x — vt, у — (tzz + Au)t). (10) Введем подвижную систему координат Ox'у , скрепленную с центром движущегося зарядового пакета: x' = x, . (11) Заметим, что uz < 0 (рис. 1) и поэтомуyf со временем возрастает. Из (11) получаем: у = У + u2t. Поэтому в подвижной системе координат (11) ФРО (10) перепишется в виде: = = f((x — vt), ( y' — Aut)). (12) Представим в (12) время t в виде суммы момента считывания зарядового пакетаCh(9,i,l) и приращения времени : t = т9 + At . С учетом последнего обозначения ФРО (12) перепишется в виде: - Ди т9 - Ди At) (13) При использовании подвижной системы коор динат (11) накопление сигнала происходит на ин - - О |О |О |O |O |O |O |O |O |O |O |O |O |O |O |O |O |O |O |O |O |O |O 3а) 3б) Рис. 3. Вид ядра “смаза” (пиксел разделен на 256 частей) Vt = (0.4; —1)[пикс]; n(ij) – область определения ядра смаза; n(i,j, t) – апертура ПЗС ячейки с номером (i,;) в момент времени t; 3 а – матрица ядра «смаза»; 3 б – ядро «смаза» в виде аксонометрической проекции полигональной поверхности (вид на поверхность сверху) тервале времени t E [(0 — q)r, 0т] в ячейке, неподвижной относительно зарядового пакета. Поэтому, с учетом (13), выражение для полного, накопленного на интервале времени №~ qX 0т], зарядового пакета СЫД i, 1) примет вид: = = z J-QT jj7T(l1) V В операторной форме (14) перепишется в виде: Ск(ОД,Г) = = ; ; [t2(x,y), tl(x,y)J: (t E [t2(x,y),tl(x,y)])O гдеK(x,y)– ядро смаза, – область определе- ния ядра смаза. Ядро смаза K(x,y) в (15) вычисляется по правилу, аналогичному (6), но в нем , а заменено на : , , (15) Использование функции веса в виде ядра сма-за K(x,y) позволяет заменить интегрирование по времени интегрированием по пространственным координатам. Это существенно упрощает вычисления. На рис. 4 представлен пример формирования ядра смаза. a) б) в) г) Рис. 4. Вид ядра смаза (апертура пиксела разделена на 256 частей) при непрерывном движении зарядового пакета по столбцу ПЗС матрицы для случая скоростей и таких, что за время накопления полного ЗП сдвиг изображения относительно ячейки накопления составил sx = 0.8 пике., sy = 1.6 пике. а – матрица числовых значений ядра ^(^y) смаза; б - треугольник векторов смещения, где а - угол сноса изображения показан для наглядности утрированно большим; в – ядро смаза, представленное полигональной поверхностью в аксонометрической проекции; г – вид полигональной поверхности ядра смаза после поворота вокруг осей Ox и Oy) Принято: - ЗП в процессе накопления заряда движется вдоль столбца матрицы с постоянной скоростью V , определяемой вектором средней скорости переноса ЗП; - полное время формирования «выходного» ЗП равно Tq; - полный сдвиг изображения относительно ЗП за время Tq его накопления составляет Sx = 0,8 пикс; 5, = 1,6пикс. В таком случае: ; ^Z = (^Z, ^zX ^ = ^, uz = 5q/xq = 5/т[пикс/с] V = (и, я), v = sx/xq [пикс/с], u = (5 + sy/q^/x [пикс/с] При этом из (1.9) ДV = V — V следует: AV = Qsx/tq, sy/Tq). Тогда за время xq : . AS = AVrq = (sx,Sy). Физика формирования ЗП в режиме ВЗН такова, что в идеальном случае ЗП всегда «догоняет» изображение. Это значит, что изображение, в идеальном случае, «бежит» впереди ЗП на одну апертуру ПЗС ячейки. Поэтому в заданном сдвиге (s-5,^ изображения избыточный сдвиг AS со-ставляетAS = (s ,5 - 1) = (0.8, 0.6)пикс. 4 X > z 4 Из рис. 4а видно что область n(ij) ненулевых значений ядра ^u,j^ (^ y) смаза вытянута вдоль вектора AS. Это означает, что именно вектор Д5 определяет формирование смаза видеоданных. ЗАКЛЮЧЕНИЕ В статье предложена модель процесса формирования смаза изображения при использовании технологии сканирования сцены «заметанием». В общем случае оператор смаза имеет вид интегрального оператора с ядром смаза, имеющим достаточно сложную конфигурацию, которая определяется вектором разности векторов СДИ и СПЗ, а также количеством активированных строк накопления матрицы. При этом ориентация области на изображении, формирующей смаз, определяется направлением вектора разности векторов СДИ и СПЗ. Работа выполнена при поддержке гранта РФФИ “офи_м” № 13-01-12014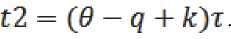
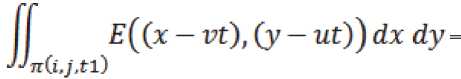
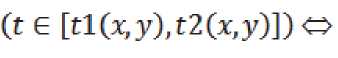
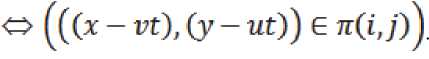
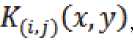
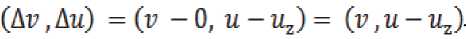
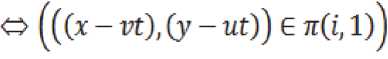
Список литературы Математическая модель формирования видеоданных, получаемых с использованием сканирующей съемки
- Злобин В.К., Еремеев В.В. Обработка аэрокосмических изображений. М.: ФИЗМАТЛИТ, 2006. 288 с.
- Егошкин Н.А., Еремеев В.В. Коррекция смаза изображений в системах космического наблюдения Земли//Цифровая обработка сигналов. 2010. № 4. С. 28-32.


