Математическая модель идеального распределения родственных популяций на неоднородном ареале

Нелинейные модели на основе уравнений реакции–диффузии–адвекции активно применяются в математической экологии для анализа пространственно распределенных популяционных систем [1–3]. При прогнозировании сценариев распространения и конкуренции видов требуются множественные расчеты при меняющихся значениях параметров. Для повышения эффективности полезно выделение классов задач, позволяющих получать информацию о решениях при некоторых идеализированных условиях. Затем можно анализировать общую ситуацию, рассматривая возмущение систем и решений. В задачах популяционной динамики таким классом являются задачи с идеальным свободным распределением (ИСР) [3].

Исходно концепция ИСР рассматривала один вид, особи которого имеют полное представление о среде обитания и могут свободно перемещаться в любую ее точку, при этом

(О 2023 Епифанов А. В., Цибулин В. Г.

динамика популяции не учитывалась. Позднее концепция ИСР была распространена на среду с двумя конкурирующими видами с учетом изменения численности популяций [4]. Обзор текущего состояния дан в [5].

Математические модели с ИСР на основе уравнений реакции–диффузии–адвекции рассматривались в ряде работ (см. [6–12]), где миграционная стратегия определялась адвективной частью потока, учитывающего перенос плотности популяции. В [6] рассмотрена модель для двух видов, учитывающая пространственные эффекты случайного блуждания и направленной миграции в направлении градиента логарифма функции ресурса. В [7] исследована система для двух видов, когда идеальной стратегией обладал один из конкурентов, и была установлена возможность сосуществования видов. Недавно для модели, описывающей динамику хищника и жертвы на неоднородном ареале, было получено аналитическое решение, отвечающее идеальному свободному распределению [13].

Подход к исследованию динамики близкородственных популяций на основе выделения идеализированных условий, обеспечивающих косимметрию рассматриваемой системы, был предложен в [14, 15]. В этих работах учитывалась направленная миграция, вызванная неоднородностью ресурса и неравномерностью распределений конкурирующих видов. Основные положения теории косимметрии В. И. Юдовича даны в цикле статей [16–18].

В данной работе рассматривается начально-краевая задача, описывающая динамику нескольких родственных видов, населяющих пространственно-неоднородный ареал. Находятся условия на дифузионные и миграционные параметры, при которых реализуется идеальное свободное распределение (ИСР), под которым понимается итоговое распределение видов, пропорциональное количеству доступного ресурса. Устанавливается косимметрия полученной системы, чтобы проанализировать сценарии при нарушении ИСР.

2.    Математическая модель

Рассматривается модель конкуренции m видов на ограниченном ареале Q С R N при неоднородной функции ресурса p (x). Для неотрицательных функций u i (x,t), обозначающих плотности конкурирующих видов в точке x = (x i ,..., x n ) G Q и момент времени t ^ 0, система уравнений имеет вид

∂u i ∂t

—V • q i + n i U i fo = F i , i = 1,..., m,

V = ( ⁸

∂

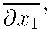
^{. ,} ∂x N

,

q i = -k i Vu i + U i V^ i ,

(x, t) G Q x (0, to) ,

1 m fo = 1 - p =2 uj •

Здесь q i — поток плотности i-го вида, n i (x) — коэффициенты роста, k i — коэффициенты диффузии, ϕ i — функция таксиса (направленной миграции):

m

^ i (x,t,U i ,U 2 , . . . ,U m ) = a i

In p(x) + УР R ij (x,t,ui ,U2, . . . ,U m ) .

j =1 , j = i

Коэффициенты αi отвечают миграции в направлении изменения плотности ресурса, функция Rij характеризует таксис вида i, вызванный неоднородностью распределения вида j. Простейшими вариантами являются линейная функция Rij = eijUj (см., например, [14]) и логарифмическая функция Rij = eij ln Uj, используемая в случае хемотаксиса.

Система (1)–(3) дополняется условиями отсутствия потоков на границе qi (x, t) • n = 0, (x, t) G d^ x (0, to) , i = 1,..., m,                      (3)

где n — внешняя единичная нормаль к границе области Q, и начальными условиями ui(x, 0) = u0(x).                                           (4)

Рассмотренная в [6, 11] система уравнений следует из (1)-(3) при m = 2, e ij = 0, n i = p (x). Приводящая к идеальному свободному распределению стратегия получается при k i = a i . В [11, 12] изучалась модификация системы (1)-(3) при m = 2, R ij = 0, k i = a i , n i = U i p(x), П 2 = p(x), когда только обладающий идеальной миграционной стратегией вид ( u 1 ) имеет слабый эффект Олли. Аналогичное исследование без эффекта Олли дано в [8], где была установлена возможность сосуществования конкурентов и нескольких положительных равновесий.

Ниже дано обобщение для случая m видов, учитывающее таксис вследствие неоднородности распределения конкурентов. Реализация ИСР возможна, если каждый вид использует стратегию, связывающую коэффициенты диффузии и направленной миграции.

Лемма 1. Система (1) - (3) при R ij = e ij ln U j и выполнении условий

m ki = ai + ^eij, i = 1,...,m,                          (5)

j=1, j=i имеет (m — 1)-параметрическое семейство стационарных решений (равновесий)

m

U i = 9 i P, ^ 9 i = 1.                                  (6)

i

⊳ Доказательство состоит в прямой подстановке решения (6) и соотношений (5) в уравнения (1), (2), (3). ⊲

В частном случае одного вида ( U j = 0, j = 2 , . . . m ) получается U i = p при условии k i = a i .

3.    Семейство равновесий и косимметрия

Для модели родственных конкурирующих видов, описываемой системой уравнений реакции-диффузии-адвекции (1)-(3), помимо тривиального равновесия Ui = 0 имеются решения, отвечающие ненулевому распределению одного вида при отсутствии других. Если имеется косимметрия — векторное поле, которое ортогонально полю системы и не аннулируется на нетривиальном равновесии, то это равновесие принадлежит непрерывному семейству стационарных состояний [16]. Обычно семейство появляется, если система имеет непрерывную симметрию, в этом случае спектр устойчивости у всех равновесий семейства одинаков. Характерной особенностью задач с косимметрией является переменность спектра устойчивости для равновесий семейства. В данной работе используется косимметрия на подпространстве, пример существования семейства стационарных решений в подобном случае дан в [19].

При учете таксиса, вызванного неоднородностью распределения конкурентов (R ij = e ij ln U j ), также возможна реализация ИСР. В следующей теореме доказывается существование косимметрии для модели (1)–(3), когда каждый вид использует стратегию (5).

Теорема 1. При R ij = e ij ln u j и условиях (5) на подпространстве

U — ^ u — (u1, • • • , um) * ui — Cip, Ci € R} система (1)–(3) имеет косимметрию

• 1    m

L = (£ 1 ,£ 2 ,-.,£ m ) , C i = — Vsigⁿ(i ^{— j)} u j .                    (7)

j

• <1 По определению косимметрии нужно показать, что (F, L) = 0, где F = (F 1 , F 2 ,..., F _m ) следует из (1). Убедимся, что ^3m= 1 Fj^ j = 0. На подпространстве U потоки равны нулю. Действительно,

n   Cj ∇p qi = -kiCi^p + aiCipV Inp + Cip ^ eij~^— = 0.              (8)

j C j p ^j= i

После перегруппировки сумма произведений компонент косимметрии на члены, отвечающие реакции, равна mm Г  i       /   i m   \    1       /    1 m

^^   ~ujniui 1 — -^ uk + “uiП3uj 1 — -^ uk  = 0

• i=1 j=i+1 L  i        X    p k=1   /     j        X    p k=1

4. Распад семейства при нарушении косимметрии

Таким образом, вектор-функция (7) действительно является косимметрией модели (1)–(3) на подпространстве U . ⊲

При этом имеется непрерывное семейство стационарных решений согласно лемме 1. Отметим, что в случае косимметрии равновесия семейства обладают индивидуальным спектром [17]. Иллюстрация для двухвидовой системы на одномерном ареале дана ниже.

В [18] предложен метод анализа решений системы при нарушении косимметрии. Для уравнения w t = Fw и возмущенного аналога w t = Fw + eKw косимметричным дефектом называется скалярное произведение D = (Kw, Lw). На решениях однопараметрического семействе ( θ — номер решения) косимметричный дефект дает селективную функцию с переменной 0. Пусть X — компактное замкнутое подмногообразие, состоящее из решений уравнения Fw = 0, и пусть, например, селективная функция имеет r нулей $1, Х2,..., x _r . Согласно теореме 2 из [18] существуют окрестность S q С X и окрестность нуля ( - 6, б) такие, что при любом e € ( — е, б) уравнение Fw + eKw = 0 имеет ровно r решений $ 1 (e) ,$2 (e) ,... ,x _r (e) в S q . Все они невырождены и аналитически зависят от ε .

Рассмотрим задачу для двух видов (т = 2), обозначая u i = u, U2 = v. В случае R j,j = 0, j = 1, 2, и R 12 = ^e i v, R 21 = Ев2и из (1)-(3) получается система, для которой нарушаются условия косимметричности:

u t = V • [k 1 V u — a1uV ln p —

ePiuVv] + n1u

—

u + v

p

,

v t = V • [k ₂ V v — a ₂ vV In p — ев2 v V u] + n2v

1 —

u + v

p

,

[k 1 V u — a1uV In p — ee1uVv] • n = 0,

[k ₂ V v — a ₂ vV In p — ee2vVu] • n = 0.

Если e = 0, то система косимметрична при условии k i = а и имеет семейство стационарных распределений [20]

u = 0p, v = (1 — 0) p.                                (11)

При ненулевом ε косимметричный дефект дается формулой

D =

[ —eiV^ uVv —

η 1

Ω

u

—e2V • vVu η 2

dx.

После интегрирования по частям и учета краевых условий (3) (потоки на границе равны нулю) получается

D =

—V — • eiuVv + V — • e 2 v V u η 1                 η 2

Ω

dx.

В результате подстановки решения для случая постоянных ηj находим селективную функцию

/ [0e2Vp- — (1 — 0 )^V ^1 η 2                  η 1

• pVpdx.

Ω

Селективная функция (14) обращается в ноль при 0 = 0, 0 = 1, что соответствует полу-положительным решениям u = 0, v = p и u = p, v = 0, а также при

» =(1 + | 2 I 2) ",   I j

= /V — • pVpdx, j = 1, 2. η j

Ω

β 1 I 1

Если 0 < 0 < 1, это отвечает решению с сосуществующими на ареале видами.

Для анализа разрушения семейства стационарных решений полезна следующая лемма.

Лемма 2. Если а = 0 , b = 0 , то двойное неравенство

0 <

a a+b

< 1

равносильно неравенству ab > 0 .

Теорема 2. Для системы (10) и возмущения

K (u, v) = e ( — e i V • uVv, — e 2 V • v V u)

от члена семейства с номером 0 < 0 < 1 ответвляется стационарное решение, если

в1 в21112 >  0.

• ⊳ Доказательство теоремы следует из леммы 2 и учета выражения для номера равновесия (15). ⊲

4. Численный анализ двухвидовой системы на одномерном ареале

Замечание. Если n i = const, П 2 = const, то при возмущении

K (u, v) = е ( - в 1 V • u V v, -в2^ • v V u)

стационарное решение ответвляется от стационарного решения семейства системы (10) с номером 0 <  9 <  1 при в 1 в 2 > 0.

Проиллюстрируем теоретические выводы результатами вычислительного эксперимента для одномерной области Q = [0, а]. По пространственной переменной проводилась дискретизация при помощи интегро-интерполяционного метода [21].

Вводилась равномерная сетка x r = rh — h/2, r = 1,..., n, h = a/n, в узлах которой определялись плотности популяций U i,_r (t). В узлах смещенной на полшага вспомогательной сетки x _{r -}i / 2 = (r — 1) h, r = 1,... ,n + 1, вычислялись потоки q i,_{r -}i / 2 . Для аппроксимации использовались операторы разностного отношения и вычисления среднего на двухточечном шаблоне для целых и полуцелых индексов:

dw r =       ■ hw r ^{- 1} / ² ,           =      ±, r = 1,...,n — 1.

В результате дискретизации уравнений (1)–(3) была получена следующая конечномерная система:

du i, dt

— dq i + n i u i

-

m

¹E p i j =1

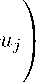
q i,r ±1 / 2 = ^{( —} k i du i ± su i ^d^ i ) r ±1 / 2, q i, 1 / 2 = q i,n ±1 / 2 = ⁰,   i = 1, •

, m,

η i,r

^x r + 1/2

n i (x) dx,

p i,r ⁼ n i,r

x r - 1/2

x r+1/2

1 /     ' dx h J P (x)

x r - 1/2

которая может быть записана в виде системы обыкновенных дифференциальных уравнений:

dY = Ф(Y), Y (0)= Y ⁽⁰⁾ , dt

W j = (U 1 ,U 2 , . . . ,U n ) j ,

Y = (W 1 , W 2 , . . . , W m ) .

Здесь Y (t) — вектор, составленный из переменных, определяемых в узлах сетки, Y ⁽⁰⁾ — начальное распределение. Интегрирование системы (19) проводилось методом Рунге — Кутты. Для расчета спектра устойчивости равновесий решалась задача на собственные значения V y Ф (Y * ) ф = А^.

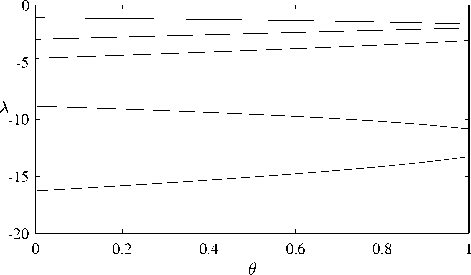
Рис. 1. Спектр устойчивости стационарных решений системы (1)–(3); m = 2, k 1 = α 1 = 0 . 4, k 2 = α 2 = 0 . 3, β i = 0.

При выполнении условий косимметрии (5) равновесия семейства обладают индивидуальным спектром. Проиллюстрируем это на примере системы двух (т = 2) видов на ареале Q = [0, а]. Далее, u i = u, U 2 = v, a = 1, П 1 =2, П 2 = 3. При R j,j = 0 и R j, 3 -j = в з ln U3 -j , j = 1, 2, имеется семейство (11).

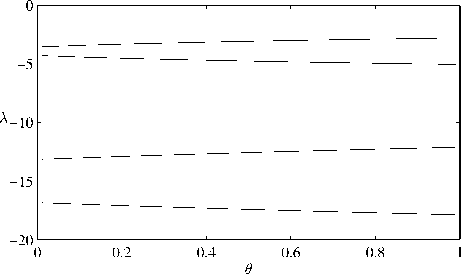
Рис. 2. Спектр устойчивости стационарных решений системы (1)–(3); m = 2 и k 1 = 0 . 4, k 2 = 0 . 3, α 1 = 0 . 43, α 2 = 0 . 31, β 1 = - 0 . 03, β 2 = - 0 . 01.

На рис. 1 приведено распределение вещественной части (А = Re ст) спектра устойчивости стационарных решений семейства при P i = 0. Каждое решение имеет одно нулевое значение, отвечающее нейтральному направлению вдоль семейства, а набор остальных спектральных характеристик зависит от континуального номера θ . Это отличает ко-симметрию от случая симметрии. На рис. 2 приведен спектр устойчивости равновесий семейства для e i = 0. В этом случае также имеется переменность спектра вдоль семейства.

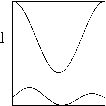
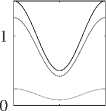
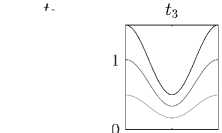
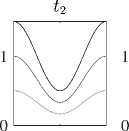
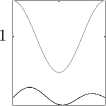
При Rii = R 22 = 0 и R 12 = ев 1 v, R 21 = ^ев 2 и покомпонентно положительное равновесие ответвляется от равновесия семейства (11) с номером 0. При в 1 = в 2 = 0.0071, p = 1 + 0.5 cos (2nx) получается 0 = 0.6. На рис. 3 приведены мгновенные профили плотностей видов системы (1)–(2). В случае инвазии вида v (вверху) и u (внизу) происходит установление к одному и тому же ответвившемуся от семейства стационарному решению, отвечающему случаю сосуществования видов. Самая верхняя кривая отвечает функции ресурса p(x).

О X 1

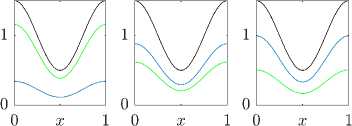
Рис. 3. Установление к изолированному решению из различных начальных данных; k i = a i = 1, k 2 = a 2 = 2, n i =2, П 2 = 3, в 1 = в 2 = 0 . 71, e = 0 . 01, p =1 + 0 . 5 cos (2 nx ).

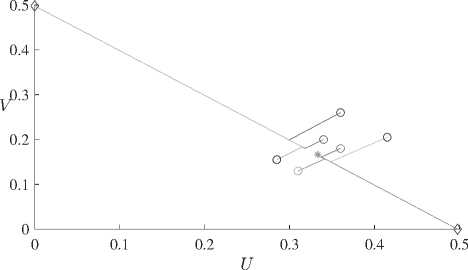
Рис. 4. Неустойчивость равновесия сосуществующих видов;

k i = a i = 1, k 2 = a 2 = 2, n i =2, П 2 = 3, в 1 = в 2 = 0 . 71, e = 0 . 01, p =1 + 0 . 5 cos (2 nx ).

На рис. 4 представлены результаты вычислительного эксперимента для системы (1)-(3) при k1 = a1 = 1, k ₂ = a ₂ = 2, в1 = в2 = - 0.0071, п1 = 2, П2 = 3, p = 1 + 0.5 cos (2nx). На плоскости параметров U = u (0.5, t), V = v (0.5, t) даны траектории, отвечающие различным начальным данным (кружки), ромбы представляют установившиеся состояния, звездочкой обозначено неустойчивое равновесие (стационарное решение), ответвившееся от семейства. Видно, что траектории из различных начальных данных быстро выходят на прямую, отвечающую исчезнувшему семейству, и далее выводят на одно из двух равновесий: (p, 0) или (0,p). Таким образом, ответвившееся от решения с номером 0 <  9 <  1 равновесие является неустойчивым, и система демонстрирует бистабильность.