Математическая модель исследования процесса разрушения двухконсольной балки

Рассматривается исследование процесса разрушения материалов на примере математической модели двухконсольной балки. Предлагается метод решения системы нелинейных уравнений, описывающих процесс разрушения двухконсольного образца. Сделаны обобщенные выводы по исследованию построенной математической модели с использованием разработанного пакета программ.

Важной задачей механики является изучение процессов разрушения материалов в результате различных внешних и внутренних воздействий, что актуально при создании любых изделий и сооружений. При создании сложных конструкций в процессе изготовления вводятся начальные деформации, что может привести к появлению трещин на каком-либо технологическом этапе. В таких случаях возникает необходимость проведения расчетов для выяснения критических размеров трещины при данной нагрузке, коэффициентов запаса по прочности и долговечности. Расчеты с учетом наличия трещин ведутся на основе критериев механики разрушения, при этом характеристики трещиностойкости оценивают сопротивлением материала распространению в нем трещины [1, 2].

Исследования проводятся на образцах, содержащих заранее созданные трещины усталости согласно ГОСТу 25.506-85. Один из распространенных образцов, на котором проводится экспериментальное определение трещиностойкости, представляет собой двухконсольную балку (ДКБ).

В статье рассматривается применение специальной информационной системы для определения параметров процесса разрушения ДКБ (рис. 1) с физическим разрезом, равным толщине слоя взаимодействия 8₀ [2], на основе варианта математической модели. По математической модели определяется критическое значение расклинивающего усилия P_k , соответствующее началу образования новых поверхностей. Начало неподвижной декартовой системы координат поместим в конце разреза. Берега разреза нагружены сосредоточенной силой P на расстоянии a от начала координат.

Необходимо определить критическое значение расклинивающего усилия P , соответствующее началу образования новых поверхностей и эпюры напряжений, отражающих взаимодействие между берегами слоя и консолями в критическом состоянии. В силу того, что учет стадии разупрочнения несущественно влияет на значение расклинивающего усилия [2], считаем, что в момент образования новых поверхностей материал слоя взаимодействия О'К'К"О" (см. рис. 1) деформируется устойчиво в смысле Дракера.

Вне слоя взаимодействия среда полагается упругой, а перемещения точек К' и К" считаются нулевыми.

В силу симметрии задачи рассмотрим только верхнюю консоль ( x 1 > 8₀/2) , а ее взаимодействие со слоем заменим искомой нагрузкой q ( x ₂) (см. рис. 2).

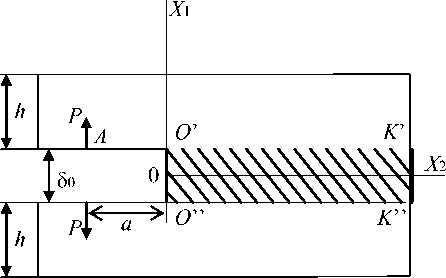
Рис. 1. Общая схема исследуемой ДКБ

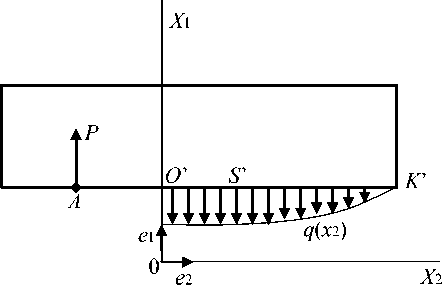
Рис. 2. Расчетная схема математической модели ДКБ

При дальнейшем изложении ограничимся случаем малых деформаций, обусловленных малостью компонент тензора-градиента вектора перемещения. В этом случае вектор внешней нагрузки на участке консоли, граничащем со слоем взаимодействия, равен:

q ( x ₂) = n • S ,                                               (1)

где S – тензор напряжений;

n = -e ₁ – вектор внешней нормали к поверхности консоли.

С учетом напряженного состояния слоя взаимодействия [2] из (1) получим:

q ( x ₂) = - S i e i .                                                   (2)

Поведение материала слоя взаимодействия рассмотрим в концепции идеально упругопластической модели [3]. В силу малости деформаций и однородности деформируемого состояния слоя взаимодействия запишем выражение компоненты линейного тензора деформаций:

ε ₁

2 u ₁ ( x ₁ ) δ 0    ,

где u ( x 2 ) - перемещение границы слоя взаимодействия ( x 1 = 8₀/2) в направлении оси OX 1 .

Из соотношений (2) и (3) с учетом преобразований [2] запишем связь между внешней нагрузкой и компонентой перемещения идеально упругопластической модели:

где E

–

q ( x ) = *

q¹ ( x ) =— 2 Eu ( x ), 5 '< x <  K'

δ 0                  ,

q¹¹ ( x ) = — 5_k , O ' <  x <  5 ' модуль Юнга материала;

Sk

[ О′S′ ] = l_p

–

–

предел текучести;

длина участка пластического деформирования.

Здесь и далее x = x₂ , u ( x ) = u 1 ( x ).

Поведение каждой консоли вне слоя взаимодействия будем описывать соотношениями теории Кирхгоффа-Лява. Уравнения изгиба для каждого из участков с учетом (4) в случае секущего модуля имеют вид (в рамках идеальной упругопластической модели):

p 3

для AO '

u ( x ) =---( a + x ) + Cx + k 2,

6 D

К

u ( x ) =

—

^kx - + C 1 x ³ + C 2 x ² + C 3 x + C 4 , для O'5' ,

u ( x ) = e

R ^{1 x} ( L i cos( R i x ) + L 2 sin( R i x )),   для O ' K '

aaa R = 4 — +- , R = 4----

.

2 Dδ  ¹   2 Dδ

Для системы (5) в критическом состоянии запишем условия непрерывности перемещения u ( x ), угла поворота u ‘ ( x ), изгибающего момента Du "( x ) и перерезывающей силы Du "'( x ) в точках O' ( x = 0) и 5 ' ( x = l_p ) . При достижении расклинивающей силой критического значения P k перемещение в точке O' достигнет значения u k = е ^{( k} ) 8₀/2, в 5' - u ₀ = е ⁽⁰⁾ 8₀/2, где е ⁽⁰⁾ - предел упругости по деформациям, а перемещение в точке A примет значение u_k^A .

Если известны экспериментальные данные критического состояния u_k ^A и P_k , то решение следующей нелинейной системы уравнений:

К

Pk 3+k -c a + ko = ca

6 D    ^{2   4}

P^a ² + k = C₃

2 D     ^{1 3}

P^a = 2 C₂

D ²

P k = 6 C₄

D ⁴

-- ^klp + Cl 3 + C₂l 2 + C ₃L + C ₄ = Le 24 D    1 p 2 p 3 p 4   1

— 1

■^Rlp cos Rl p + 5 ₂ e ^Rlp sinRl p

—

—

—

—

S k l ³ p 6 D S k l ² p 2 D S k l p D S k l ⁴ p

+ 3 C 1 l p + 2 C ₂ l_p + C ₃ = Re ^p [— L 1 (cosRl_p + sin Rl p )+ L 2 (cosRl p — sin Rl p )]

+ 6C 1 l_p + 2 C 2 = 2 R ² e ^Rlp [ L 1 sin Rl p — L 2 cos Rl p ]

+ 6 C 1 = 2 R ³ e ^Rlp ( L 1 (cos Rl_p — L 2 sin Rl p )+ L 2 (cosRl_p + sin Rl p )

24 D

+ Cl 3p + C 2 I p + C 3 l_p + C 4 = e ⁽⁰ % ₀ / 2

k 2 — k i a = u k

пдахёёо iidaaaeeou д1ёйё^6 пё1у 5₀ ё aёё^6 giru хёапдё^апёшх аад1д1ёдшМёу l шдуао n ппдхупшё ё^дaaдёд1aа^ёy k 1 , k ₂, L 1 , L ₂, C 1 - C ₄.

В отсутствие прямых экспериментальных данных по разрушению ДКБ-образцов вычислим, основываясь на решении (5) для участка пластического деформирования, толщину слоя взаимодействия. Следуя концепции квазихрупкого разрушения, поток энергии в вершину слоя G может быть определен в рамках линейного решения. Удельную (к единице образуемой поверхности а ) работу на разрушение бесконечно малого объема в вершине разреза A вычислим исходя из полученного решения (5). Следуя концепции квазихрупкого разрушения, запишем:

G = A .

Рассмотрим бесконечно малое приращение поверхности разрыва а . Работа в материальном объеме а5₀ (на единицу толщины образца) может быть найдена:

αε ( x )

A ' = J J 8 0 S _k dedx ,

где e ( x ) - деформация слоя в критическом состоянии.

В силу идеальной упругопластической модели поведения материала слоя взаимодействия, выражение (7) может быть представлено в следующем виде:

а        ^e y

A ' = J 0.5 S_k J 8 0 de + S k

0 (        0

^{e (} x ⁾

J ⁸ 0 de dx , ^e y J

где e _y - предел упругости по деформациям.

Из (8) работа может быть определена:

α

A ' = J ( 8 0 S k e ( x )) dx — 0.5 S k e _y8 0 «.                                (9)

С учетом однородности напряженного деформированного состояния (НДС) в слое взаимодействия деформация определена в виде (3). Следовательно, работа на единицу длины образуемой поверхности из (9) может быть найдена:

2 ^α

A = lim —J S k u ( x ) dx — 0.5 S k e _y8 0 , а ^ 0 а 0                ^y

—

где u ( x ) =

S x ⁴      3      2

^^ + Cix^ + C 2 x^L + C 3 x + C 4 в силу решения (5).

Таким образом, для данной модели получаем следующее выражение:

A = 2 S k C 4 — 0,5 S k e y 5 0 .

Константу интегрирования C ₄ определим из условия достижения перемещением в точке O ‘ (рис. 2) критического значения u k = e ^{( k )} 5₀/2 :

C k = u_t = e^{( k} ' d , /²-

Из равенств (7), (11), (12) приходим к следующему результату для толщины слоя взаимодействия:

5 0

K I ² C

SkE (e (k) — 0,5e y)’

Следовательно, для материалов с выраженными пластическими свойствами е ^{( к} ) < е y , справедливо выражение:

K ic — 4S_kE3_k ,

где 8 _к = е ^{( k} ) 8 0 - критическое смещение слоя взаимодействия.

Выражение (14) совпадает с представлением вязкости разрушения через критерий Леоно-ва-Панасюка, Дагдейла [1], если ассоциировать 8 _к с критическим раскрытием трещины, а S k - с напряжением взаимодействия между берегами трещины.

Из (13) получаем следующую оценку:

K_I ² _C

S_kE^- k ) ~ 0 '

Заменим в системе (6) последнее уравнение условием достижения критического перемещения в точке O' и_к = е ^{( k} ) 8₀/2 :

P k _a 6 D P k a

2 D

+ к 2 - C 4

+ к 1 - C 3

P^a — 2 C₂

D ²

P k

--— 6 C

D

^- S k l p 24 D

+ C 1 l p + C ₂ l p + C 3 l p + C 4 — L 1 e ^Rlp cos Rl_p + S ₂ e Rl p sin Rl_p

S k i p + 3 C 1 1 p + 2 C ₂ l_p + C 3 — Re ^Rlp [ - L 1 (cos Rl p + sin Rl p ) + L ₂(cos Rl p

- sin Rl p )]

-S ^ -p- + 6 C,l „ + 2 C ₂ — 2 R ² e~^Rlp [ L sin RU - L ₂ cos Rl_n ] 1 p 2                  1 p 2 p

Sip + 6 C 1 — 2 R ³ e ^Rlp ( L 1 (cos Rl_p - L ₂ sin Rl_p ) + L ₂ (cos Rl_p + sin Rl_p )

S k^lp + Cl 3 + C₂l 2 + C₃l„ + C ₄ — £ ⁽⁰⁾ ^ ) /2 1 p 2 p 3 p 4         0

P^a ³ + k ₂ — £ ^{( k} ) 3₀ /2

1 б D      ^{2       0}

В результате получена система нелинейных уравнений для определения длины пластической зоны l_p , критического усилия P_k , а также постоянных интегрирования k ₁, k ₂, L ₁, L ₂, C ₁– C ₄.

Решение полученной системы нелинейных уравнений сведем к решению множества систем линейных уравнений путем присвоения переменной l_p фиксированного значения, подбираемого методом дихотомии. Этот метод обладает медленной скоростью сходимости, но зато точность ответа гарантируется.

С использованием разработанной информационной системы проведен ряд исследований, позволивших сделать следующие выводы:

• 1.    Высота консоли (рис. 1) существенно влияет на длину пластической зоны слоя взаимодействия. В случае варьирования плеча существует широкий диапазон, при котором l_p не меняется.

• 2.    При учете пластических свойств материала в виде (5) падение напряжения за пределом зоны пластичности происходит быстрее в менее жестких материалах.

• 3.    Рассмотрение модели поведения слоя взаимодействия, кривые напряжение-деформация которых ограничивают реальную кривую испытания на растяжение, приводит к результату (15) для оценки толщины слоя взаимодействия. Для более точного определения толщины слоя необходимо учитывать прямые экспериментальные данные.